Вопрос 33
35 .Тригонометрическим рядом Фурье называют функциональный ряд вида;
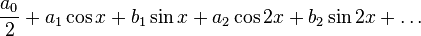
коэффициенты,
которого вычисляются по формулам

Теорема: Если
периодическая функция 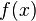 с
периодом
с
периодом 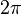 —
кусочно-монотонная и ограниченная
на отрезке
—
кусочно-монотонная и ограниченная
на отрезке 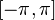 ,
то тригонометрический ряд Фурье,
построенный для этой функции, сходится
во всех точках. Сумма полученного
ряда
,
то тригонометрический ряд Фурье,
построенный для этой функции, сходится
во всех точках. Сумма полученного
ряда 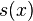 равна
значению функции
в
точках ее непрерывности. В точках
разрыва
сумма
ряда равняется среднему арифметическому
пределов функции
справа
и слева
равна
значению функции
в
точках ее непрерывности. В точках
разрыва
сумма
ряда равняется среднему арифметическому
пределов функции
справа
и слева
Пусть
-
периодическая функция 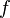 абсолютно
интегрируема на отрезке
абсолютно
интегрируема на отрезке 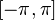 ,
и существует
,
и существует 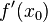 .
Тогда ряд Фурье функции
сходится
в точке
.
Тогда ряд Фурье функции
сходится
в точке 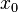 к
к 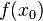 Ряд
Фурье на [-L;L]
Ряд
Фурье на [-L;L]
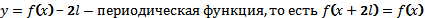
Замена переменной:
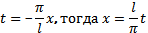
По переменной t – период
2π
то это ряд вида .
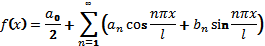


26




