2.2. Энергия Гиббса и энергия Гельмгольца

В процессе, протекающем при постоянной температуре и давлении, критерием направления процесса и равновесия является изменение энергии Гиббса G. Изменение энергии Гельмгольца A служит аналогичным критерием при постоянной температуре и объеме. При необратимом самопроизвольном протекании процесса изменение энергии Гиббса и энергии Гельмгольца уменьшаются, т. е.

; ; (2.17)

; . (2.18)

При обратимом протекании процесса или в состоянии равновесия изменение энергии Гиббса и энергии Гельмгольца равно нулю

; . (2.19)

Приращение обеих энергий при постоянной температуре может быть рассчитано по формулам:

; (2.20)

. (2.21)

Изменение энергии Гиббса и Гельмгольца равно максимальной полезной работе, взятой с обратным знаком, соответственно изобарно-изотермического или изохорно-изотермического процесса

; . (2.22)

При расширении или сжатии n молей идеального газа при постоянной температуре изменение энергии Гиббса, равное в данном случае изменению энергии Гельмгольца, определяется из выражения

. (2.23)

Изменение энергии Гиббса для фазовых переходов

. (2.24)

Для химических реакций (T = const)

, (2.25)

где – сумма энергий Гиббса для продуктов реакции и исходных веществ.

П р и м е р. Определить изменение энергии Гиббса и максимальную полезную работу при изотермическом сжатии 7 г азота от 0,50610⁵ до 3,0410⁵ Па при температуре 27 C. Газ считать идеальным.

Решение. Изменение энергии Гиббса рассчитываем по уравнению (2.23)

,

которое с учетом (1.27) принимает вид

.

После подстановки числовых значений, получим

Так как связь между энергией Гиббса и максимальной полезной работой определяется уравнением (2.22), то

.

3. Химическое равновесие

При протекании химической реакции через некоторое время устанавливается равновесное состояние (химическое равновесие), которое не является статическим, т. е. состоянием покоя. Химическое равновесие это такое состояние системы, когда скорости прямой и обратной реакции становятся одинаковыми.

При изменении внешних условий равновесие сдвигается и возвращается в исходное состояние, если внешние условия приобретают первоначальные значения.

Химическая термодинамика позволяет предсказать концентрации реагентов в равновесной реакционной смеси и влияние на них изменения внешних условий, а также предвидеть максимальный выход полезного продукта, что имеет большое практическое значение.

3.1 Закон действующих масс

Математическим выражением законов термодинамики для равновесия химических процессов является закон действующих масс, который формулируется следующим образом: отношение произведения равновесных концентраций (или парциальных давлений) продуктов реакции, взятых в степенях, равных их стехиометрическим коэффициентам, к аналогичному произведению для исходных веществ при данной температуре есть величина постоянная (константа равновесия).

Константа равновесия химической реакции, протекающей в смеси идеальных газов по уравнению

_AA + _BB = _DD + _EE, (2.26)

имеет следующий вид

, (2.27)

где _A, _B, _D, _E – стехиометрические коэффициенты участвующих в реакции веществ A, B, D, E;

K_P – константа химического равновесия;

p_D, p_E, p_A, p_B – равновесные парциальные давления продуктов реакции и исходных веществ.

Константа равновесия K_P не зависит от давления. Учитывая соотношение между парциальным давлением (p_i, Па), концентрацией (c_i, моль/м³) и молярной долей (x_i) газа i-го сорта

, (2.28)

можно получить также выражения для константы равновесия химической реакции в виде

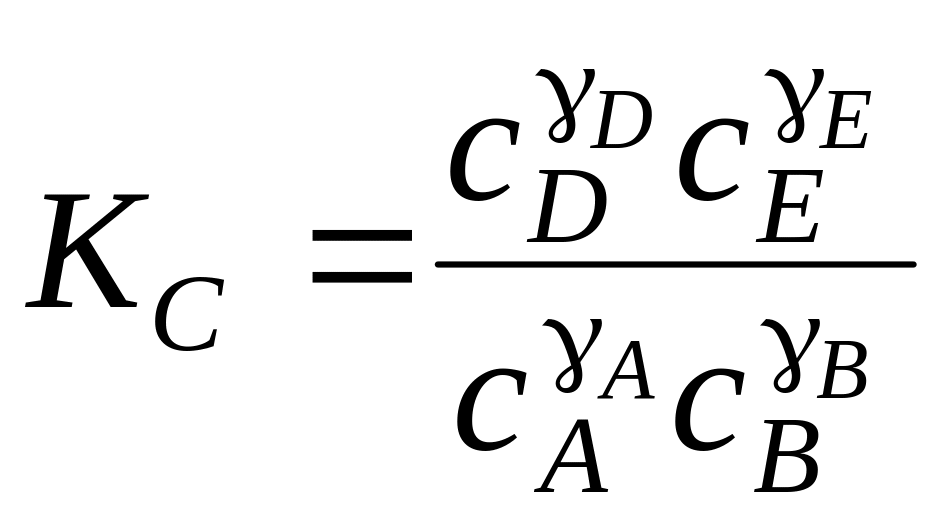; (2.29)

, (2.30)

где P – общее давление;

n_i – число молей i-го компонента;

n_i – общее число молей реагентов в равновесной газовой смеси.

Константы равновесия связаны соотношением

, (2.31)

где  – разность между стехиометрическими коэффициентами конечных и начальных газообразных веществ в соответствии с уравнением реакции (2.26).

. (2.32)

Уравнения (2.29), (2.30) могут быть использованы также для расчета равновесия химических реакций в идеальных растворах.

Для гетерогенных реакций с участием твердых и жидких фаз константа равновесия K_P выражается только отношением равновесных парциальных давлений газообразных реагентов, так как активность вещества в чистой твердой или жидкой фазе принимается равной единице. Например, для реакции

_AA_т + _BB_г = _DD_г (2.33)

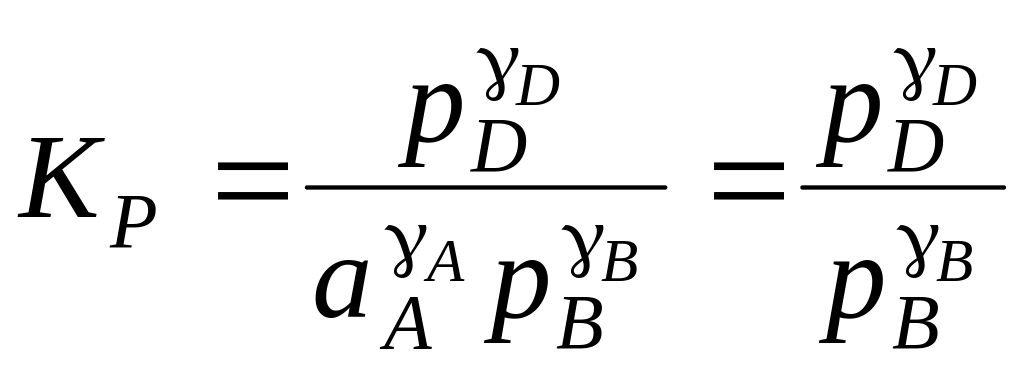, (2.34)

где – активность чистого твердого вещества A.

Константу равновесия химической реакции можно вычислить косвенным методом, пользуясь стандартными изменениями энергии Гиббса. В уравнение, связывающее стандартные изменения энергии Гиббса, подставляют известные константы равновесия

(2.35)

и решают его относительно неизвестной константы.

Стандартная константа равновесия связана с константой равновесия соотношением

, (2.36)

где  – приращение числа молей во время реакции, которое определяется по выражению (2.32).

Если выражены в атмосферах (все = 1 атм), то = 1 и = , т. е. константы равновесия и имеют одно и то же значение. Если выражены в Па (все = 1,01310⁵ Па), то = (1,01310⁵)^; размерность [ ] = Па^.

П р и м е р. Вычислить при температуре 298 K константу равновесия реакции (1.47)

CO + 0,5O₂ = CO₂,

используя справочные данные о тепловых эффектах образования и об абсолютных энтропиях (табл. 2).

Таблица 2

Стандартные термодинамические величины CO₂, CO и O₂

Вещество	CO2	CO	O2
, кДж/моль	– 393,51	– 110,50	0
, кДж/(мольK)	213,6	197,4	205,03

Решение. Из уравнения (2.35) имеем

.

Стандартную энергию Гиббса реакции находим по (2.20). Для реакции, идущей при 298 K и 0,101310⁵ Па,

, (2.37)

где

,

= .

Подставив в (2.37) числовые значения, получим

,

.

Учитывая соотношение (2.36), при  = – 0,5 находим

Большое значение указывает на то, что при стандартных условиях равновесие рассматриваемой реакции сильно сдвинуто вправо.