9. Уравнение прямой с заданным угловым коэффициентом. Уравнение прямой, проходящей через 2 точки.

Уравнение линии на плоскости называется такое уравнение относительно двух переменных, которому (1) удовлетворяет координаты любой точки, лежащей на данной линии и не удовлетворяет любой другой точки, не лежащей на данной линии. F(x;y)=0 (1)

Уравнение прямой с заданным угловым коэффициентом.

1. Y=kx+b, k=tgα= 2) y-y₀=k(x-x₀)

Общее уравнение прямой:

Любую точку на плоскости можно задать линейным уравнением относительно х и у, где А и В – это действительные числа, причём А²+В²≠0

Ax+By+C=0, A(x-x₀)+B(y-y₀)=0

Уравнение прямой, проходящей через две точки.

10. Общее уравнение прямой на плоскости.

Общее уравнение прямой:

Любую точку на плоскости можно задать линейным уравнением относительно х и у, где А и В – это действительные числа, причём А2+В2≠0

Ax+By+C=0, A(x-x0)+B(y-y0)=0

Уравнение Ax+By+C=0, где А²+В²≠0, задаёт прямую на плоскости

1. В≠0, у=

2. А=0, В и С≠0, Ву+С=0, у=-

3. В=0, А и С≠0, Ах+С=0, х=-

4. А≠0, В≠0, С=0, Ах+Ву=0, у=-

5. А≠0, В≠0, С≠0, Ах+Ву+С=0, Ах+Ву=- С

11. Параметрическое и каноническое уравнения прямой на плоскости.

Параметрическое уравнение прямой на плоскости

Параметрические уравнения прямой могут быть записаны следующим образом

x=l t+x₀

y=m t+y₀

где (x₀,y₀) - координаты точки лежащей на прямой,{l,m}- координаты направляющего вектора прямой.

Каноническое уравнение прямой на плоскости

Если известны координаты точки A(x₀,y₀) лежащей на прямой и направляющего вектора ={l;m}, то уравнение прямой можно записать в каноническом виде, используя следующую формулу

(l,m)- направляющий вектор

12. Взаимное расположение прямых на плоскости. Расстояние от точки до прямой.

Расстояние от точки до прямой

d=

Взаимное расположение прямых на плоскости:

1. Р₁IIP₂

2. P₁ P₂

tgα=tg(α₂-α₁), tgα= =

1 случай: Р1IIP2, k₁=k₂

2 случай: P₁ P₂, k1*k2=-1

13. Уравнение плоскости в пространстве. Взаимное расположение прямых в пространстве.

Уравнение плоскости проходящей через току М₀ (х₀, у₀, z₀)

A(x-x₀)+B(y-y₀)+C(z-z₀)=0

Общее уравнение плоскости

Ax+By+Cz+D=0

Уравнение плоскости в отрезках

, где

Уравнение плоскости, проходящей через 3 точки

Взаимное расположение двух прямых в пространстве

Р1:

P2:

1 случай: Р1IIP2→ II →

2 случай: P1∩P2=

3 случай: Р1 и Р2 скрещивающиеся, ≠0

14. Взаимное расположение прямой и плоскости в пространстве.

Прямая и плоскость в пространство могут:

а) не иметь общих точек;

б) иметь ровно одну общую точку;

в) иметь хотя бы две общие точки.

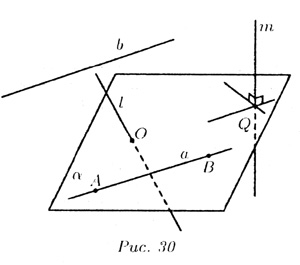
В случае а) прямая b параллельна плоскости : b || .

В случае б) прямая l пересекает плоскость в одной точке О; l = О.

В случае в) прямая а принадлежит плоскости : а или а .