6. Коэффициент корреляции

Парный коэффициент корреляции (коэффициент корреляции Пирсона) показывает направление и тесноту линейной связи между двумя количественными показателями, распределение которых в генеральной совокупности близко к нормальному. Формула расчета коэффициента корреляции следующая:

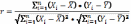
согласованное поведение может объясняться тремя причинами:

1. Показатель Х влияет на показатель Y

2. Показатель Y влияет на показатель X

3. Показатель Z влияет на показатели X и Y, заставляя их вести себя согласованно.

Подчеркнем, что коэффициент корреляции, отличный от 0, лишь «констатирует факт» согласованного повеления показателей, но НИЧЕГО не говорит о том, что является тому причиной.

8Парный линейный регрессионный анализ

Главной целью регрессионного анализа является изучение связи между факторным признаком и результативным показателям.

Уравнение парной линейной регрессии имеет вид:

y_i=a+b*x_i+e_i,

где y –результативный показатель, x- факторный показатель, a, b – параметры уравнения регрессии, e- ошибка. Регрессия называется парной, так как используется один факторный показатель и один результативный показатель. Регрессия называется линейной, так как аналитическая форма связи между факторным и результативным показателями - линейная функция.

Параметры уравнения a, b находят посредством МНК (метода наименьших квадратов), при котором в качестве решения принимается точка минимума суммы квадратов отклонений эмпирических данных y_i от расчетных 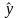_i, рассчитанных по модели, т.е.

Σ(y_i –a-bx_i)²  min

Для нахождения минимума данной функции, ее частные производные приравнивают нулю и из полученной системы находят формулы для вычисления a и b.

Коэффициент b показывает, насколько в среднем изменяется величина результативного признака (в его единицах измерения) при изменении факторного признака на единицу (в его единицах измерения).

Параметр a показывает усредненное влияние прочих факторов на результативный показатель.

9Оценка качества уравнения регрессии. Расчет коэффициента детерминации и множественного коэффициента корреляции.

Рассчитать значения a и b можно для любого набора значений двух показателей. Для оценки того, насколько хорошо уравнение регрессии описывает данные, рассчитывается коэффициент детерминации, основанный на следующем тождестве:

Общая сумма квадратов = Регрессионная(объясненная) сумма квадратов + Остаточная сумма квадратов.

Здесь Y_i- фактические значения результативного признака, - расчетные значения результативного признака, получаемые путем подстановки x_i в уравнение регрессии: Y_i=a+b*X_i

Общая сумма квадратов оценивает всю вариацию результативного показателя, регрессионная (объясненная) сумма квадратов показывает вариацию расчетных значений результативного относительно среднего значения результативного показателя, остаточная сумма квадратов характеризует расхождение между расчетными и фактическими значениями результативного показателя.

Регрессионная (объясненная) сумма квадратов показывает вариацию результативного показателя, обусловленную вариацией факторного показателя.

Остаточная сумма квадратов показывает вариацию результативного показателя, которую нельзя объяснить вариацией факторного показателя.

Коэффициент детерминации рассчитывается как отношение объясненной суммы квадратов к общей сумме квадратов. Коэффициент детерминации показывает, какая часть вариации результативного показателя объясняется вариацией факторного показателя. Коэффициент детерминации может изменяться от 0 до 1. Чем ближе коэффициент детерминации к 1, тем лучше уравнение регрессии.

Множественный коэффициент корреляции рассчитывается как парный коэффициент корреляции между фактическими и прогнозными значениями результативного показателя.

Множественный коэффициент корреляции и коэффициент детерминации связаны следующим соотношением: квадрат множественного коэффициента корреляции равен коэффициенту детерминации. В то же время, множественный коэффициент корреляции равен по модулю коэффициенту корреляции между факторным и результативным показателем.