
- •1. Данные. Классификация данных в зависимости от шкалы измерения
- •4 Выборочный метод и теория оценивания
- •Характеристики центральной тенденции и вариации переменной
- •Коэффициент корреляции
- •8Парный линейный регрессионный анализ
- •9Оценка качества уравнения регрессии. Расчет коэффициента детерминации и множественного коэффициента корреляции.
- •10. Тест Фишера:
- •11. Тест Стьюдента
- •12. Расчет доверительного интервала для β
- •Основные понятия и определения
- •Диверсификация как способ управления риском капиталовложения
- •Уравнение связи между ожидаемой нормой доходности и риском
- •Нахождение регрессионных коэффициентов.
- •Оценка качества уравнения регрессии. Расчет коэффициента детерминации и множественного коэффициента корреляции.
- •Тест Фишера:
- •Тест Стьюдента
- •Расчет доверительного интервала для βj
- •Расчет стандартизованных регрессионных коэффициентов
- •Механизм возникновения проблемы мультиколлинеарности
- •23. Симптомы мультиколлинеарности:
- •24. Методы диагностики проблемы мультиколлинеарности:
- •25. Борьба с мультиколлинеарностью путем изменения состава факторов
- •25. Алгоритм пошагового включения:
- •26. Алгоритм пошагового исключения
- •I. Однофакторные нелинейные модели регрессии и их линеаризация
- •28. Гиперболические модели
- •29. Полулогарифмические модели
- •30. Степенная модель
- •31. Экспоненциальная модель
- •32. Логистическая модель
- •33. Логлинейная модель
- •II. Многофакторные нелинейные модели регрессии и их линеаризация
- •34. Критерии выбора лучшей формы связи
- •35. Расчет коэффициентов эластичности
- •Эффект масштаба
- •Эффект обучения
- •Эконометрическая оценка эффектов масштаба и обучения
29. Полулогарифмические модели
3.1.
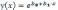 .
Для линеаризации используется методы
логарифмирования и замены переменных.
Прологарифмировав левую и правую части
этого уравнения, получаем:
.
Для линеаризации используется методы
логарифмирования и замены переменных.
Прологарифмировав левую и правую части
этого уравнения, получаем: 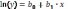 .
Рассчитываем новую переменную z=ln(x)
(т.е. фактически
вычисляется дополнительный столбец z
по формуле zi=ln(xi))
и задача поиска регрессионных коэффициентов
этой нелинейной модели сводится к задаче
поиска регрессионных коэффициентов
однофакторной линейной модели z=b0+b1*x+.
.
Рассчитываем новую переменную z=ln(x)
(т.е. фактически
вычисляется дополнительный столбец z
по формуле zi=ln(xi))
и задача поиска регрессионных коэффициентов
этой нелинейной модели сводится к задаче
поиска регрессионных коэффициентов
однофакторной линейной модели z=b0+b1*x+.
Графиком этой функции является экспоненциальная кривая (рис.4). Как видно из графика, при x>0 рассматриваемая функция подходит для моделирования прямых зависимостей как с увеличивающейся скоростью роста (если b1>0, то имеем дело с монотонно возрастающей вогнутой функцией) и обратных зависимостей с уменьшающейся скоростью падения (если b1<0, то имеем дело с убывающей вогнутой функцией).
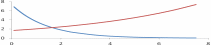
Рис.4. График функции
3.2.
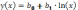 Для линеаризации
используется метод замены переменных:
z=ln(x)
(т.е. фактически вычисляется дополнительный
столбец z
по формуле zi=ln(xi))
и задача поиска регрессионных коэффициентов
этой нелинейной модели сводится к задаче
поиска регрессионных коэффициентов
однофакторной линейной модели y=b0+b1*z+.
Для линеаризации
используется метод замены переменных:
z=ln(x)
(т.е. фактически вычисляется дополнительный
столбец z
по формуле zi=ln(xi))
и задача поиска регрессионных коэффициентов
этой нелинейной модели сводится к задаче
поиска регрессионных коэффициентов
однофакторной линейной модели y=b0+b1*z+.
График рассматриваемой функции приведен на рис.5. Как видно из графика, при x>0 рассматриваемая функция подходит для моделирования прямых зависимостей как с уменьшающейся скоростью роста (если b1>0, то имеем дело с монотонно возрастающей выпуклой функцией) и обратных зависимостей с уменьшающейся скоростью падения (если b1<0, то имеем дело с убывающей вогнутой функцией).

Рис.5. График функции
30. Степенная модель
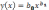
Для
линеаризации используются методы
логарифмирования и замены переменных.
Прологарифмировав левую и правую части
этого уравнения, получаем:  .
Рассчитываем новые переменные z1=ln(x)
и z2=ln(y)
(т.е. фактически
вычисляем дополнительные столбцы z1
по формуле z1i=ln(xi)
и
z2
по формуле z2i=ln(yi)
). Рассчитываем
регрессионные коэффициенты однофакторной
линейной модели
.
Рассчитываем новые переменные z1=ln(x)
и z2=ln(y)
(т.е. фактически
вычисляем дополнительные столбцы z1
по формуле z1i=ln(xi)
и
z2
по формуле z2i=ln(yi)
). Рассчитываем
регрессионные коэффициенты однофакторной
линейной модели 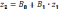 .
Затем определяем регрессионные
коэффициенты степенной модели:
.
Затем определяем регрессионные
коэффициенты степенной модели: 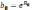 ,
b1=B1.
,
b1=B1.
Поведение функции в зависимости от значений параметров описано в таблице.
b0 |
b1 |
Возрастание или убы- вание |
Выпук-лость или вогну-тость |
Характер зависимости |
> 0 |
>0 и <1 |
монотонно возраста-ющая |
выпуклая |
Прямая зависимость с уменьшающейся скоростью роста, результирующий показатель принимает только положительные значения |
> 0 |
>1 |
монотонно возраста-ющая |
вогнутая |
Прямая зависимость с увеличивающейся скоростью роста, результирующий показатель принимает только положительные значения |
> 0 |
< 0 |
монотонно убывающая |
вогнутая |
Обратная зависимость с уменьшающейся скоростью падения, результирующий показатель принимает только положительные значения |
< 0 |
>0 и <1 |
монотонно убывающая |
вогнутая |
Обратная зависимость с уменьшающейся скоростью падения, результирующий показатель принимает только отрицательные значения |
< 0 |
>1 |
монотонно убывающая |
выпуклая |
Обратная зависимость с увеличивающейся скоростью падения, результирующий показатель принимает только отрицательные значения |
< 0 |
<0 |
монотонно возраста-ющая |
выпуклая |
Прямая зависимость с уменьшающейся скоростью роста, результирующий показатель принимает только отрицательные значения |
График рассматриваемой функции при различных сочетаниях значений параметров приведен на рис.6.

Рис.6. График функции
