Плотность тока

В электротехнике часто бывает важно знать не только силу тока в проводнике, но и плотность тока, так как плотность тока является мерой допустимой нагрузки проводов.

Плотностью тока называют ток    , приходящийся на единицу площади проводника:  , где

- сила тока

- площадь поперечного сечения проводника

 - плотность тока, выражается в амперах на квадратный метр:  .

Физическая величина, равная работе сторонних сил при перемещении единичного положительного заряда q от отрицательного полюса источника тока к положительному, называется электродвижущей силой источника (ЭДС):

Суммарная ЭДС батареи последовательно соединенных источников равняется сумме ЭДС этих источников:

Напряжение на участке цепи, содержащем источник тока, определяется формулой:

где r – внутреннее сопротивление источника.

Закон Ома и Джоуля-Ленца в дифференциальной форме.

Если в проводнике течет постоянный ток и проводник остается неподвижным, то работа сторонних сил расходуется на его нагревание. Опыт показывает, что в любом проводнике происходит выделение теплоты, равное работе, совершаемой электрическими силами по переносу заряда вдоль проводника. Если на концах участка проводника имеется разность потенциалов   , тогда работу по переносу заряда q на этом участке равна 

По определению . откуда . Следовательно 

Так как работа идет па нагревание проводника, то выделяющаяся в проводнике теплота Q равна работе электростатических сил

(1)

Соотношение (1) выражает закон Джоуля-Ленца в интегральной форме. Введем плотность тепловой мощности   , равную энергии выделенной за единицу время прохождения тока в каждой единице объема проводника

где S - поперечное сечение проводника,   - его длина. Используя (1) и соотношение   , получим

Но   - плотность тока, а   , тогда

с учетом закона Ома в дифференциальной форме  , окончательно получаем

(2)

Формула (2) выражает закон Джоуля-Ленца в дифференциальной форме: объемная плотность тепловой мощности тока в проводнике равна произведению его удельной электрической проводимости на квадрат напряженности электрического поля.

Билет № 20.

Расчет магнитной цепи постоянного магнита.

Постоянные магниты широко применяются в измерительных приборах, реле, генераторах и т. д.

На рис.1.4 изображено тороидальное кольцо с воздушным зазором.

Рис.1.4. Тороидальный магнитопровод с воздушным зазором (а) и его кривая размагничивания (б)

Если бы не было воздушного зазора, то, как видно из кривой размагничивания (рис.1.4б), напряженность в сердечнике равнялась бы нулю H_c=0, а индукция B_c в сердечнике равнялась бы остаточной индукции B₀.

Из закона полного тока имеем:  .

Здесь

 - магнитное напряжение воздушного зазора;

l_c - длина средней линии тороида.

Напряженность магнитного поля в воздушном зазоре:  .

Если зазор достаточно мал, то можно пренебречь потоком рассеяния и считать, что поток в магните равен потоку в зазоре:  ,

отсюда

;  .

Воспользовавшись выражением  можно написать:

;

;

(1.9)

 

коэффициент  носит название размагничивающего фактора.

Проведем прямую H_c= -NB_c из точки 0 до пересечения с кривой размагничивания (рис.1.4б). Координаты точки пересечения  определяют напряженность магнитного поля H_c и индукцию B_c. Если теперь уменьшить величину зазора, то магнитная индукция и напряженность будут определяться не кривой размагничивания, а, в силу наличия гистерезиса, частной петлей гистерезиса. Эту петлю называют линией возврата.

Билет № 21.

Переменный ток в цепи с конденсатором. Ток смещения.

Конденсатор в Цепи Переменного Тока.

Если конденсатор включить в цепь постоянного тока, то в цепи возникает кратковременный импульс тока, который заряжает конденсатор до напряжения источника, а затем ток прекращается. Если заряженный конденсатор отключить от источника постоянного тока и соединить его обкладки с выводами лампы накаливания, то конденсатор будет разряжаться, при этом наблюдается кратковременная вспышка лампы.

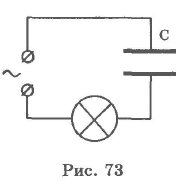
При включении конденсатора в цепь переменного тока процессы зарядки и разрядки конденсатора чередуются с периодом, равным периоду колебаний приложенного переменного напряжения, и лампа накаливания (рис. 73), включенная последовательно с конденсатором, кажется горящей непрерывно, так как человеческий глаз при промышленной частоте колебаний силы тока не замечает периодического ослабления свечения нити лампы.

При изменениях напряжения на обкладках конденсатора по гармоническому закону

U = U_mcos(wt) (4.16) заряд на его обкладках изменяется по закону:

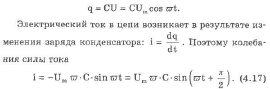
Из сравнения (4.16) и (4.17) следует два вывода: ток по фазе на ПИ/=2 при разрядке конденсатора опережает колебания напряжения на его обкладках и емкостное сопротивление хс, равное отношению амплитуды напряжения на конденсаторе к амплитуде силы тока, равно:

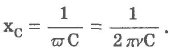
Емкостное сопротивление обратно пропорционально емкости конденсатора и циклической частоте переменного тока.

Емкостное и индуктивное сопротивления называют реактивными. Это означает, что на них не происходит превращение электрической и магнитной энергии во внутреннюю, т. е. тепловую.

В вакууме, а также в любом веществе, в котором можно пренебречь поляризацией либо скоростью её изменения, током смещения   (с точностью до универсального постоянного коэффициента) называется поток вектора быстроты изменения электрического поля   через некоторую поверхность  :

 (СИ)

 (СГС)

В диэлектриках (и во всех веществах, где нельзя пренебречь изменением поляризации) используется следующее определение:

 (СИ)

 (СГС),

где D — вектор электрической индукции (исторически вектор D назывался электрическим смещением, отсюда и название «ток смещения»)

Соответственно, плотностью тока смещения в вакууме называется величина

 (СИ)

 (СГС)

а в диэлектриках — величина

 (СИ)

 (СГС)

В некоторых книгах плотность тока смещения называется просто «током смещения».