Билет № 42.

Определим проекции вектора Пойнтинга в цилиндрической системе координат, так как вектор напряженности магнитного поля ориентирован по касательной к цилиндрическому проводнику с током, т.е. в цилиндрической системе координат имеет составляющую только, то вектор Пойнтинга не будет иметь такой проекции. При этом Пz=ErHα; Пr=EzHα.

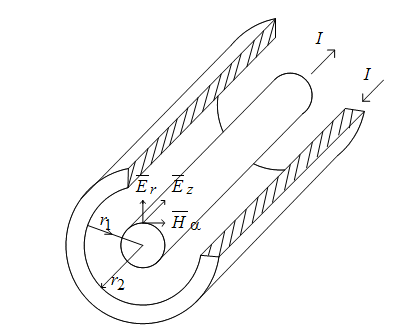
Рис. 18.2. Отрезок коаксиального кабеля

Напряженность электрического поля в диэлектрике определяется зарядом и током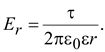

Напряжение между жилами кабеля

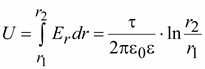
.Следовательно, на поверхности жилы

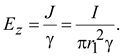
По закону полного тока

Тогда

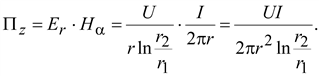
Из формулы видно, что плотность потока энергии имеет наибольшее значение вблизи жилы

Рис. 18.3. К определению плотности тока энергии

За пределами кабеля магнитного поля нет (H=0).

В пределах оболочки нет радиальной составляющей вектора поля, следовательно, нет потока.

Угловая и радиальная составляющие напряженностей имеются только в кольцевом сечении диэлектрика.

Следовательно, энергия в осевом направлении передается по зазору в кабеле, а проводники служат как направляющие для потока.

Радиальная составляющая вектора Пойнтинга на поверхности жилы

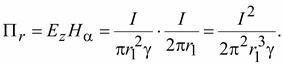
Полагая, что плотность тока энергии на поверхности жилы одинакова, найдем энергию

т.к.

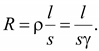
Следовательно, радиальная составляющая вектора Пойнтинга определяет потери энергии в проводнике при протекании по нему тока.

43 Вопрос.

Отражение электромагнитных волн - изменение направления распространения электромагнитной волны на границе двух сред, при котором падающая на границу раздела волна частично или полностью возвращается в первую среду. Полное отражение падающей волны происходит на поверхности идеального проводника. В реальных проводниках, обладающих некоторым сопротивлением, часть энергии падающей волны поглощается. Частичное отражение наблюдается на границе двух диэлектриков с различной скоростью распространения электромагнитных волн. В этом случае волна частично проникает в диэлектрик. Иногда на границе двух диэлектриков может происходить полное отражение волн (см. Полное внутреннее отражение). Отражение электромагнитных волн от поверхности хорошего проводника можно рассматривать как отражение от идеального проводника. При падении электромагнитной волны на поверхность идеального проводника поле волны вызывает движение носителей электричества в проводнике, и в его поверхностном слое возникают электрические токи с частотой падающей волны.

- это среднее по времени от модуля вектора плотности потока энергии:

Для гармонической волны:

При наложении двух встречных плоских волн с одинаковой амплитудой возникает колебательный процесс, называемый стоячей волной. При этом переноса энергии не происходит.

Для волны, бегущей по оси x:

Для волны, бегущей против оси x:

Для простоты мы положили равным нулю значение начальных фаз этих волн. Сумма этих уравнений и дает уравнение стоячей волны:

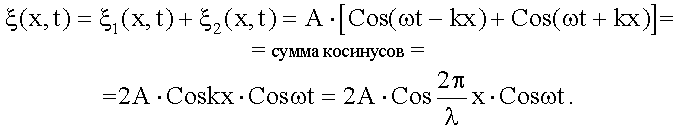
- это модуль выражения, стоящего перед множителем Cosωt, т.е.

Поверхность, где амплитуда колебаний равна нулю, называют узлами стоячей волны. Для узлов:

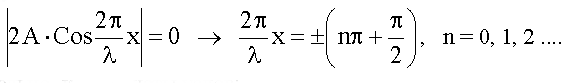
Следовательно, координаты узлов:

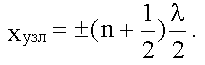
Поверхность, где амплитуда колебаний достигает максимума, называют пучностями стоячей волны.

Для пучностей:

Координаты пучностей: