Билет № 1.

Силовая картина взаимодействия. Электрическая и магнитная силы. - магнитная сила - электрическая сила

Сравним взаимодействие зарядов (сила Кулона) и токов, образованных этими зарядами (сила ампера) в параллельных проводниках. 

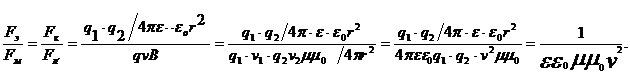
 Магнитное поле, действующее на заряд, создается другим зарядом, движущимся относительно первого. Предположим, что ν₁=ν₂, заряды находятся на расстоянии r друг от друга. Возьмем перпендикулярно , то есть , тогда по закону Био – Савара - Лапласа выражаем  с учетом этого получили выражение для F_э/F_м.  Известно, что _. Пусть среда вакуум. Тогда если ε=1, μ=1,  Получим .

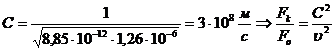 Следствия:

1.Электрическая сила больше магнитной по величине.

2.Магнитная сила принимает существенные значения, когда скорости зарядов близки к скорости света. Если бы С

3.Поскольку скорость света конечна, магнитная сила релятивистская, то есть проявляет себя при скоростях, близких к скорости света.

Билет № 2.

Магнитное поле движущегося заряда. Закон Био-Савара-Лапласа.

Магнитная индукция   — векторная величина, являющаяся силовой характеристикой  магнитного поля(его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой  магнитное поле действует на заряд  , движущийся со скоростью  .

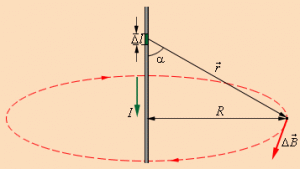
Закон Био-Савара-Лапласа — физический закон для определения вектора индукции магнитного поля , порождаемого постоянным электрическим током .

Билет № 3.

Сила Лоренца. Сила Ампера. Определение направления этих сил на примерах.

Сила, действующая на проводник с током в магнитном поле, называется силой Ампера. Сила действия однородного маг­нитного поля на проводник с током прямо пропорциональна силе тока, длине проводника, модулю вектора индукции магнитного поля, синусу угла между вектором индукции магнитного поля и проводником: F=B^.I^.ℓ^. sin α — закон Ампера. Направление силы Ампера (правило левой руки): Если левую руку расположить так, чтобы перпендикулярная составляющая вектора В входила в ладонь, а четыре вытянутых пальца были направлены по направлению тока, то отогнутый на 90° большой палец покажет направление силы, действующей на проводник с током. Сила, действующая на заряженную движущуюся частицу в магнитном поле, называется силой Лоренца:  Направление силы Лоренца (правило левой руки) Направление F определяется по правилу левой руки: вектор F перпендикулярен векторам В и v.. Правило левой руки сформулировано для положительной частицы. Сила, действующая на отрицательный заряд будет направлена в противоположную сторону по сравнению с положительным.

Билет № 4.

Теорема о потоке вектора напряженности электрического поля (т.Гаусса). Пример. Поток вектора напряженности через произвольную замкнутую поверх­ность равен алгебраической сумме зарядов, заключенных внутри этой поверхности, деленной на ε₀ (ε₀ - электрическая постоянная)

 

Применение теоремы Гаусса. Напряженность поля, создаваемая бесконечно протяженной однородно заряженной плоскоти с поверхностной плотностью заряда σ. Поверхностная плотность заряда показывает, какой заряд приходится на единицу площади 1. Линии напряженности  перпендикулярны рассматриваемой поверхности и направлены от нее в обе стороны. Построим цилиндр с основанием S, образующая которого параллельна линиям напряженности .

 

 

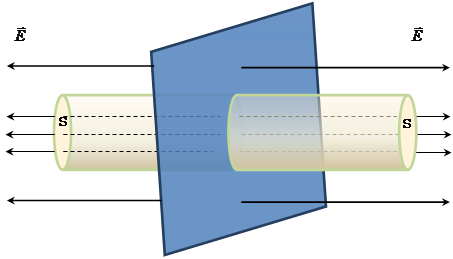Так как образующая цилиндра параллельна   , то поток через основание S равен

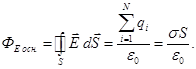
Поток через боковую поверхность цилиндра равен нулю, т.к.  перпендикулярна S cosα= cos90° = 0, следовательно,

2. Напряженность поля, создаваемая двумя параллельными бесконечно протяженными пластинами с поверхностной плотностью зарядов +σ и -σ. Найден поле Е, используя принцип

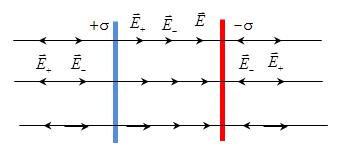суперпозиции полей. В области между плоскостями

Слева и справа от плоскостей поля вычитаются, т.к. линии напряженности направлены навстречу друг другу  .

 

Билет №5.

Теорема о циркуляции вектора индукции магнитного поля (т. Стокса). Пример.

Т еорема: Циркуляция вектора по произвольному замкнутому контуру L равна произведению µ₀ (магнитной постоянной) на алгебраическую сумму токов, охватываемых контуром:

В ывод формулы:

Обобщение:

С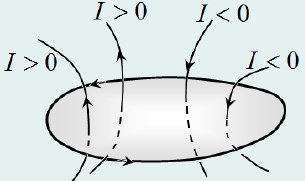 умма токов, пересекающих контур

понимается в алгебраическом смысле, то есть токи могут быть положительными, так и отрицательными. Сила тока считается положительной, если его направление и направление обхода образуют правый винт.

Так же, как и поток, циркуляция является интегральной (не точечной) характеристикой магнитного поля − из того, что циркуляция по какому-то контуру равна нулю, не следует, что магнитное поле отсутствует (может контур не охватывает ни один ток, или их сумма равна нулю). Токи, не пересекающие контур, так же создают магнитное поле, но циркуляция этого поля по такому контуру равна нулю.

Пример:

Рассчитаем, применяя теорему о циркуля­ции, индукцию магнитного поля внутри соленоида. Рассмотрим соленоид длиной l, имеющий N витков, по которому течет ток (рис. 175). Длину соленоида считаем во много раз больше, чем диаметр его витков, т. е. рассматриваемый соленоид бесконечно длинный.

Н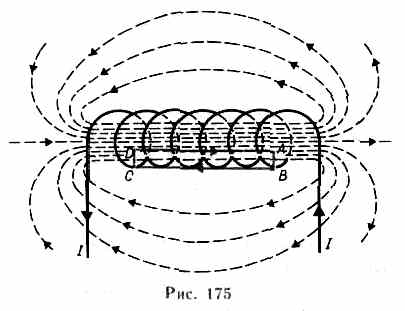 а рис. 175 представлены линии маг­нитной индукции внутри и вне соленоида. Чем соленоид длиннее, тем меньше маг­нитная индукция вне него. Поэтому при­ближенно можно считать, что поле бес­конечно длинного соленоида сосредоточе­но целиком внутри него, а полем вне соленоида можно пренебречь.

Для нахождения магнитной индукции В выберем замкнутый прямоугольный кон­тур ABCDA, как показано на рис.175. Циркуляция вектора В по замкнутому кон­туру ABCDA, охватывающему все N вит­ков равна

Интеграл по ABCDA можно представить в виде четырех интегралов: по АВ, ВС, CD и DA. На участках АВ и CD контур перпендикулярен линиям магнитной ин­дукции и В₁=0. На участке вне соленоида В=0. На участке DA циркуляция векто­ра В равна Вl (контур совпадает с линией магнитной индукции); следовательно,

Таким образом, уравнение теоремы о циркуляции в данном случае имеет вид

где N − число витков обмотки, которые попали внутрь выбранного контура. Из этого уравнения находим индукцию магнитного поля внутри соленоида.

где − число витков обмотки на единицу длины соленоида (плотность намотки).

Из окончательной формулы следует, что поле внутри длинного соленоида является однородным.

Билет №6.

Потенциал электрического поля. Связь напряжённости и потенциала. Пример.

Электростатический потенциал - скалярная энергетическая характеристика электростатического поля, характеризующая потенциальную энергию, которой обладает единичный положительный пробный заряд, помещённый в данную точку поля.

Единицей измерения потенциала в Международной системе единиц (СИ) является вольт

1В = 1Дж/Кл.

Электростатический потенциал равен отношению потенциальной энергии взаимодействия заряда с полем к величине этого заряда:

Напряжённость электростатического поля и потенциал связаны соотношением:

и ли обратно:

Где — оператор набла.

В прямоугольных декартовых координатах это равенство расписывается как

П ример: Поле заряда, равномерно распределённого по поверхности сферы радиуса R с поверхностной плоскостью

Система зарядов и, следовательно, само поле центрально-симметричны относительно центра О сферы. Вектор напряжённости поля имеет только радиальную составляющую

,

где - радиус-вектор, проведённый из центра О сферы в рассматриваемую точку поля; - проекция вектора Е на радиус-вектор, одинаковая во всех точках, равноудалённых от центра О. Поэтому за гауссову поверхность S следует взять сферу радиуса r с центром в точке О. Тогда

Если r R, то q_охв=q и по теореме Остроградского-Гаусса

Если r<R, то q_охв=0 и E_r=0, т.е. внутри заряженной сферы поля нет.

Потенциал поля найдём из формулы связи между потенциалом и напряжённостью поля:

Полагая, что , получаем, что потенциал поля вне сферы равен:

Из этих формул видно, что вне заряженной сферы радиуса R поле такое же, как поле точечного заряда q, находящегося в центре сферы. Внутри заряженной сферы поля нет, так что потенциал всюду одинаков и такой же, как на её поверхности:

Графики зависимостей E_r и от r для случая, когда

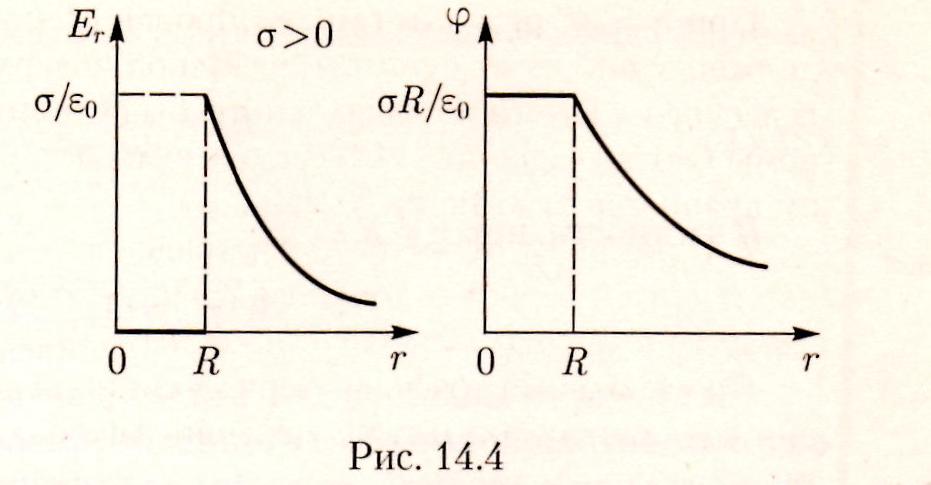
Билет №7.

Напряжённость и потенциал электрического поля заряженной по поверхности сферы.

Система зарядов и, следовательно, само поле центрально-симметричны относительно центра О сферы. Вектор напряжённости поля имеет только радиальную составляющую

,

где - радиус-вектор, проведённый из центра О сферы в рассматриваемую точку поля; - проекция вектора Е на радиус-вектор, одинаковая во всех точках, равноудалённых от центра О. Поэтому за гауссову поверхность S следует взять сферу радиуса r с центром в точке О. Тогда

Если r R, то q_охв=q и по теореме Остроградского-Гаусса

Если r<R, то q_охв=0 и E_r=0, т.е. внутри заряженной сферы поля нет.

Потенциал поля найдём из формулы связи между потенциалом и напряжённостью поля:

Полагая, что , получаем, что потенциал поля вне сферы равен:

Из этих формул видно, что вне заряженной сферы радиуса R поле такое же, как поле точечного заряда q, находящегося в центре сферы. Внутри заряженной сферы поля нет, так что потенциал всюду одинаков и такой же, как на её поверхности:

Графики зависимостей E_r и от r для случая, когда

Билет №8.

Напряжённость и потенциал электрического поля заряженного по объему шара.

Центр шара О является центром симметрии поля. Поэтому для гауссовой поверхности S в виде сферы радиуса r с центром в точке О

где - проекция вектора Е на радиус-вектор r, проведённый из точки O в рассматриваемую точку поля;

. Связь между потенциалом и напряжённостью поля:

Если r R, то q_охв=q и

В частности, при r=R

Если r<R, то и

Из связи между и E следует, что для r < R

так что

Графики зависимостей E_r и от r для случая, когда

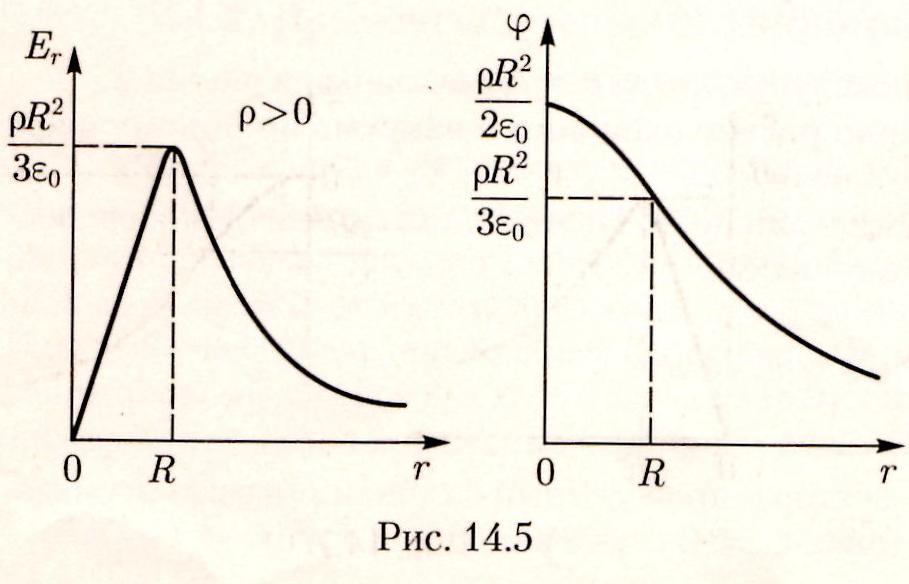
Билет № 9.

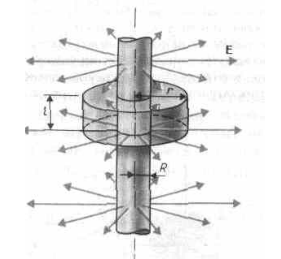
Напряжённость и потенциал электрического поля заряженной по поверхности трубы.

Для решения нужно построить коаксиальных конечный цилиндр большего радиуса r.

В нутри поля нету, т.к. противонаправленные заряды компенсируют друг друга; вне трубы вычисляется согласно формуле площади поверхности цилиндра: . Поток через боковую поверхность цилиндра равен

Потенциал же внутри постоянен и не изменяется; а учитывая, что , получаем, что потенциал снаружи

R

R

r

r

Билет № 10.

Напряжённость и потенциал электрического поля заряженной по объёму цилиндра.

Для решения нужно построить коаксиальных конечный цилиндр большего радиуса r. Зная, что . Снаружи цилиндра заряд, попавший внутрь поверхности интегрирования Q, равен - исходя из формулы объёма цилиндра. Объёмная плотность заряда

Внутри же

Для того, чтобы рассчитать потенциал внутри:

И вне его:

В итоге, считая, что , получаем:

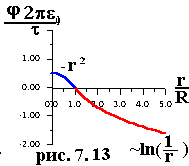
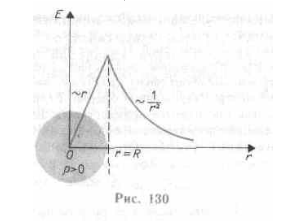
Билет № 11.

Магнитное поле цилиндрического проводника с равномерным по сечению током.

В силу симметрии линии вектора Н являются окружностями, плоскости которых перпендикулярны к оси провода. Центры этих окружностей лежат на оси цилиндра. На одинаковых расстояниях от оси цилиндра численное значение вектора Н одно и то же.

Рассмотрим линию вектора Н внутри провода. Циркуляция Н_вн по этой линии равна охваченному току:

Так как Н_вн вдоль контура интегрирования имеет одинаковое численное значение и направлена по касательной к линии L, то

Приравняв циркуляцию и полный ток, получим:

  (1)

На поверхности проводника напряженность поля имеет наибольшее значение.

Если контур интегрирования L провести вдоль линии вектора H вне провода, циркуляция Н_вш равна току в проводе:

Следовательно,

(2)

Выражения (1), (2) позволяют определить напряженность магнитного поля в любой точке пространства как внутри провода, так и вне его.

Билет № 12.

Электрический диполь. Электрический диполь во внешнем электрическом поле.

Э

l

лектрический диполь — система двух равных по модулю разноименных точечных зарядов (-q,+q), расстояние l между которыми значительно меньше расстояния до рассматриваемых точек поля.

В однородном электрическом поле вектор напряженности имеет одно и то же направление в любой точке и на диполь будут действовать силы F+ и F-. Очевидно, что эти силы равны по модулю F+= F-=q*E и противоположны по направлению. Они образуют пару сил, плечо которой равно l*sinα. Модуль момента этой пары сил равен произведению силы и плеча M=q*E*l*sinα=P*E*sinα.

О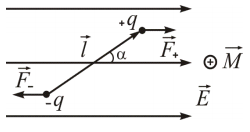 днородное электрическое поле стремится повернуть диполь таким образом, чтобы векторы P и E стали параллельными. При повороте на угол a энергия диполя измениться на величину:

При α=π/2 потенциальная энергия равна нулю, а значит и постоянная интегрирования C=0. И тогда W=-P*E*cosα. Существуют два положения равновесия диполя в однородном электростатическом поле: когда векторы P и E параллельны и антипараллельны. В первом

случае α=0, соответственно cos0=1, потенциальная энергия отрицательна. Во втором случае cos180=-1 и потенциальная энергия положительна. Состояние устойчивого равновесия соответствует минимуму потенциальной энергии системы, или по-другому это означает, что при выведении системы из равновесия возникают силы, которые стремятся вернуть ее в первоначальное состояние.

В таком поле диполь будет поворачиваться до устойчивого состояния. Однако поскольку сила, действующая на отрицательный заряд больше за силу, действующую на положительный заряд (F->F+), то диполь будет втягиваться в более сильное поле.

Равнодействующая этих сил равна