26. Інтегральна ознака Коші.

.Нехай члени ряду a₁+a₂+a₃+…+a_n+…(1)додатні і не зростають, тобто a₁≥a₂≥a₃≥…≥a_n≥…(1’) і нехай f(x) така неперервна не зростаюча функція, що f(1)=a₁, f(2)=a₂, f(3)=a₃,…, f(n)=a_n,…(2). Тоді даний ряд і невласний інтеграл 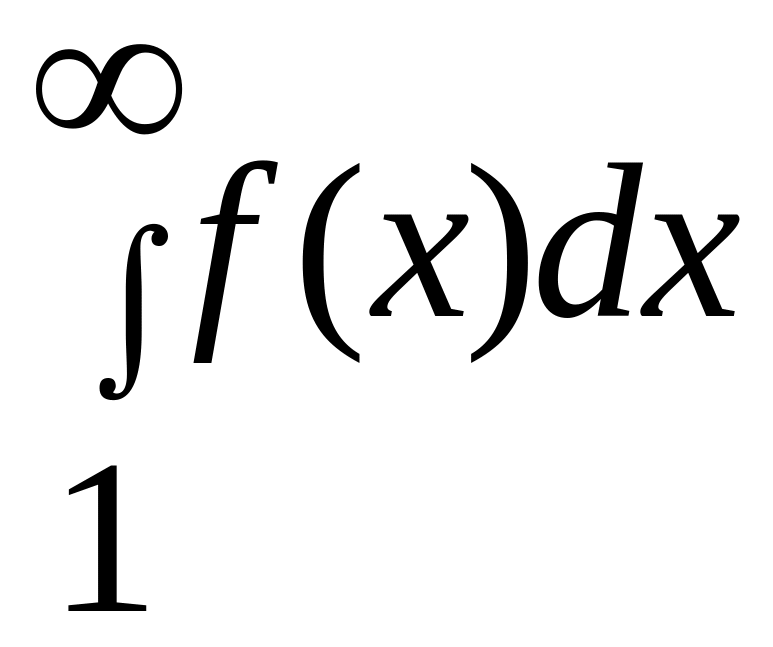одночасно збігається або розбігається. Доведення. Зобразимо члени ряду геометрично, відкладаючи на осі Ox номери 1,2,3,…,n+1,…членів ряду, а на осі Oy відповідні значення членів ряду a₁,a₂,a₃,…,a_n+1,…

Побудуємо на цьому ж рисунку графік неперервної, не зростаючої функції y=f(x),що задовольняє умову(2). Замітимо, що перший із побудованих прямокутників має основу, що дорівнює 1 і висоту f(1)=a₁. Другий прямокутник основу – 1, висоту f(2)=a₂ і т.д.n-ий – основу – 1, а висоту f(n)=a_n. Сума площ побудованих прямокутників дорівнює S_n і дорівнює сумі перших n–членів ряду, тобто S_n= a₁+a₂+…+a_n. З іншої сторонни ступінчата фігура, що складається з прямокутників містить в собі площу обмежену лініями: y=f(x),y=0,x=1,x=n+1. Площа цієї області визначається за формулою: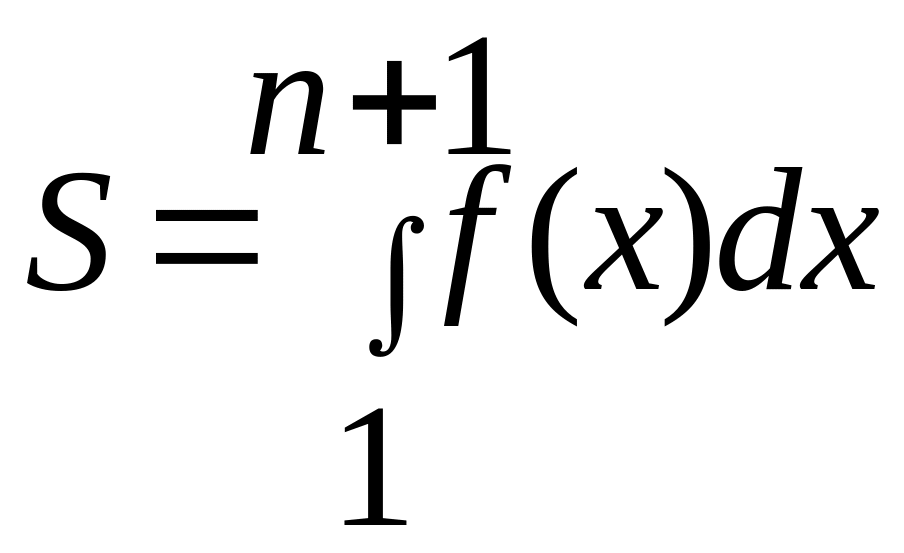 . Отже, 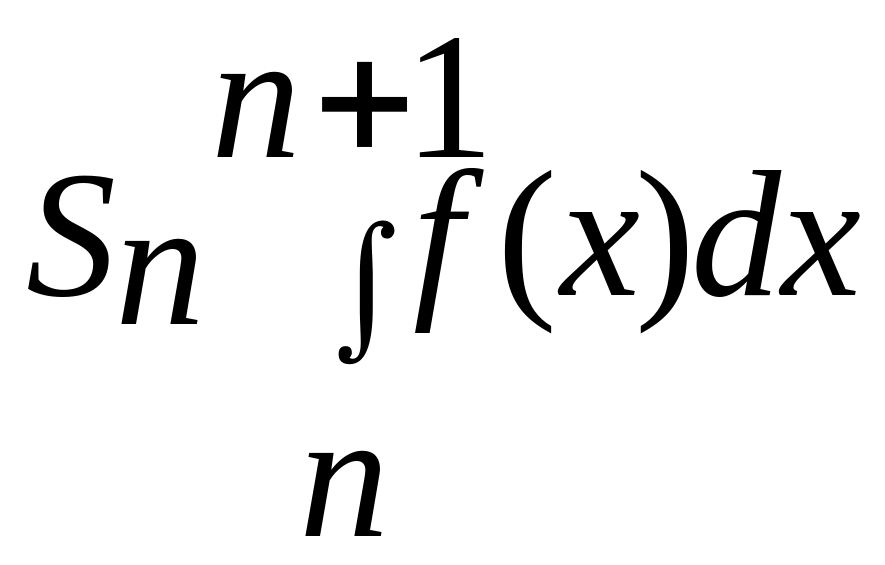. Якщо невласний інтеграл є розбіжним, то він дорівнює 1 і якщо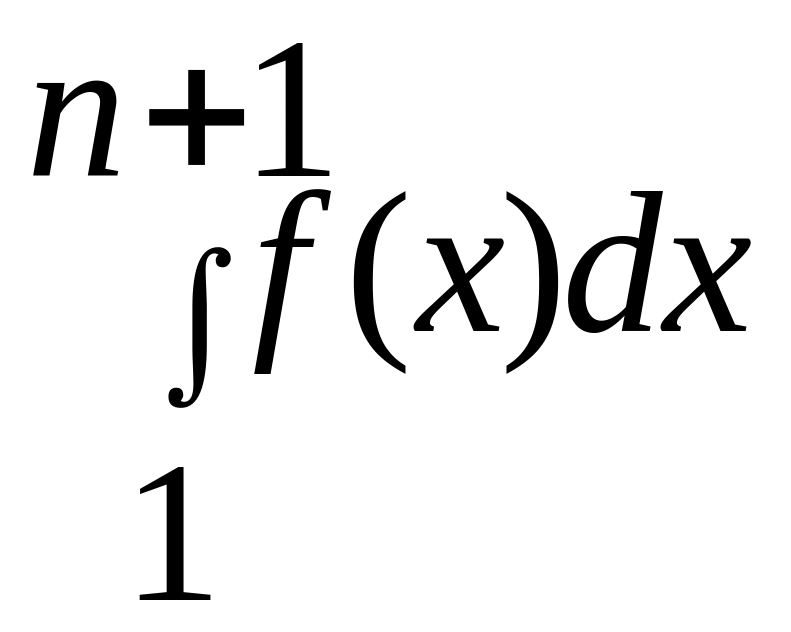 є необмеженим і зростає з необмеженим зростанням n. Тоді і послідовність частинних сум необмежено зростає, тобто , отже, ряд є розбіжним.

Розглянемо тепер рисунок 2:

На осі Ох відкладено номери 1, 2, 3, 4, 5, …,n+1 членів ряду, а на осі Оу відповідні значення членів ряду. На рисунку 2 перший із побудованих прямокутників має основу 1, а висоту f(2)=a₂. Другий – основу 1, висоту f(3)=a₃. Третій – основу 1, висоту f(4)=a₄ і т.д. n–ий – основу 1, а висоту - f(n+1)=a_n+1. Сума площ всіх побудованих прямокутників дорівнює сумі всіх членів ряду починаючи з 2 до n+1, тобто a₂+a₃+a₄+…+a_n+1=S_n+1-a₁. З іншої сторони ступінчаста фігура, що складається з прямокутників міститься всередині криволінійної трапеції, що обмежена лініями: y=f(x), y=0, x=1, . Площа криволінійної трапеції визначається за формулою: . Із рис.2 видно, що S_n+1-a₁< звідси випливає S_n+1< +a₁. Припустимо що інтеграл 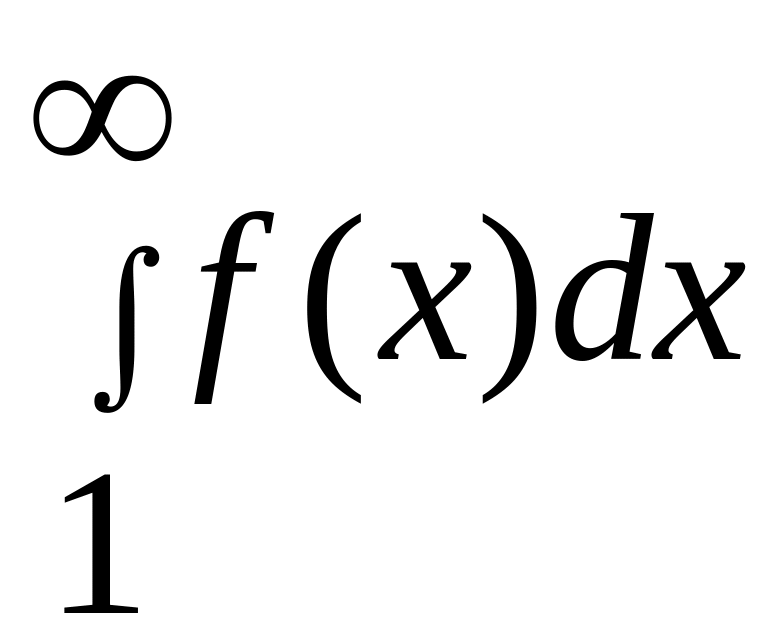збігається, а це означає, що 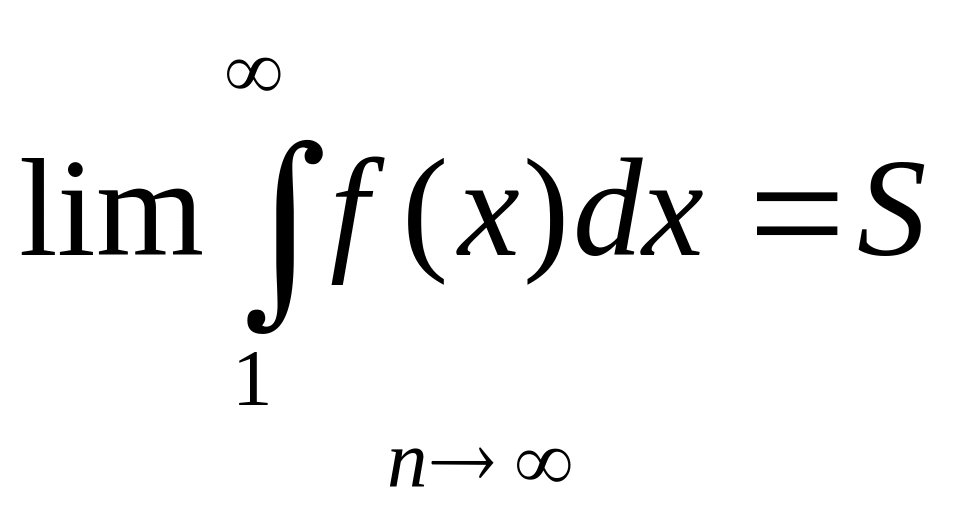. Так як 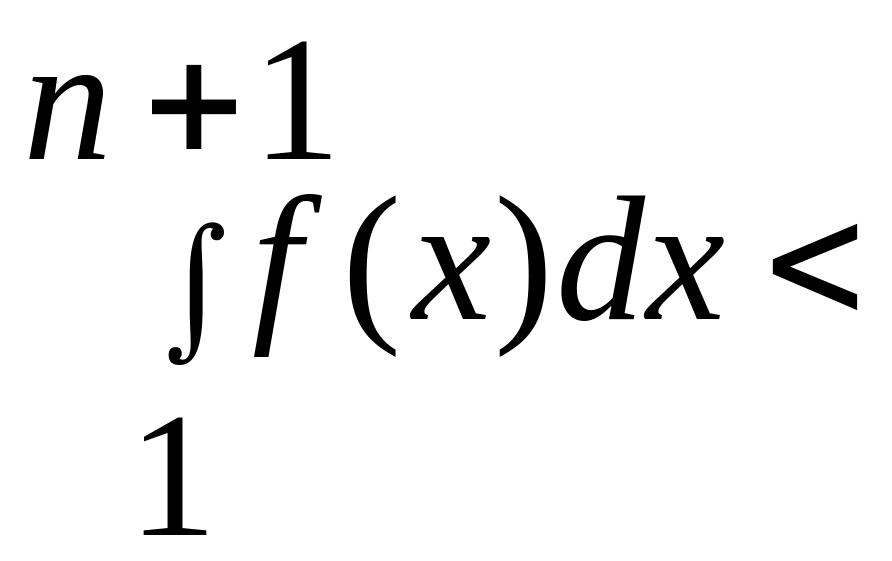, то S_n<S_n+1<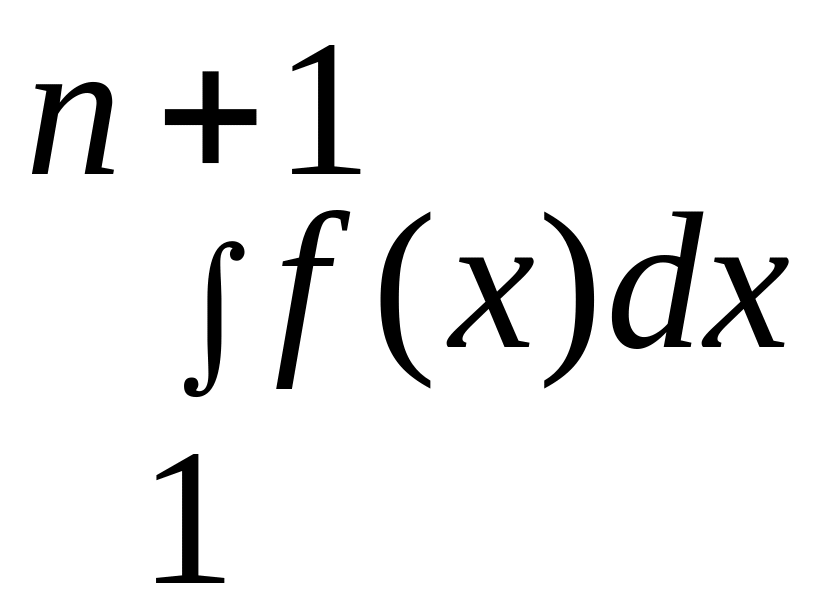 +a₁<S+a₁.Так як частинна сума S_n залишається обмеженою при всіх значеннях n, але при збільшенні n вона зростає, так як всі члени a_n додатні, то частинна сума S_n має скінченну границю , отже, ряд збігається.

27. Знакопочережні ряди. Теорема Лейбніца

Ряди, члени яких мають особливість знакочергуватися, тобто ряди виду: а1-а2+а3-а4+...+(-1)^n-1аn+…..(1), де а1, а2, а3,....-додатні наз знакочергуючим рядом.

Теорема Лейбніца: Якщо в знакочергуючому ряді члени ряду такі, що

1)|a1|>|a2|>….>|an|>…

2)lim|an|=0

nà0

то ряд (1) збігається, його сума додатня і не більша першого члену ряду. Тобто:

S<=a1

Доведення

Розглянемо суму перших n=2m членів ряду(1), тобто візьмемо парну кіл-ть членів.

S_2m=(а1-а2)+(а3-а4)+(а5-а6)+...+(а_2m-1-a_2m)

Із умови 1) теореми Лейбніца випливає, що вираз в кожних дужках >0. Отже S_2m>0

S_2m=a1-(а2-а3)-(а4-а5)-(а6-а7)-...-(а_2m-2-a_2m-1)-a_2m.

В силу умови 1) теореми вираз в кожних дужках>0. Тоді:S_2m<a1. Отже послідовність частинних сум S_2m зростає і обмежена, а отже має:

limS_2m=S

mà0

Таким чином ми показали, щ S>0, але S<a1. Тобто послідовність парних частинних сум має своєю границею число S. Покажемо, що непарні частинні суми також мають своєю границею число S. Розглянемо суму перших n=2m+1 членів ряду.

S_2m+1 =S_2m+a _2m+1

Знайдемо:

limS_2m+1=lim(S_2m+a_2m+1)=limS_2m+lima_2m+1=S+lima_2m+1=S+0=S

nà∞ mà∞ mà∞ mà∞ mà∞

Ми показали, що при n=2m і n=2m+1 границя частинної суми ряду = S. Отже ряд збігається.

Зауваження 1: теорема Лейбніца справедлива і в тому випадку, коли нерівності 1 виконуються, починаючи з деякого №n.

Зауваження 2:Якщо знакочергуючий ряд задовольняє умові теореми, то неважко оцінити помилку, яку ми допускаємо при заміні суми ряду S на часткову суму S_n. При такій заміні ми відкидаємо всі члени ряду, починаючи з аn+1 члена ряду. Але всі ті числа, що ми відкидаємо теж утворюють знакочерг ряд, сума якого за абс велечиною менше першого члену цього ряду, тобто менше an+1. Значить помилка, яку ми допускаємо при заміні S на Sn не більша за абсолютну велечину першого із відкинутих членів ряду.