20.Неоднорідні лінійні диференціальні рівняння 2-го порядку зі сталими коефіцієнтами.

Нехай потрібно знайти загальний розв’язок р-ня у”+py’+qy =f(x). (1)

Загальний розв’язок неоднор. р-ня = сумі загал. розв’ язку відповідного р-ня без правої частини y”+py’+qy =0 (2) і якого-небудь частинного розв’ язку даного р-ня.

Як знайти заг. розв’ язок однор. р-ня відомо. Укажемо спосіб знаходження частинного розв. р-ня (1). Розглянемо метод невизначених коефіцієнтів. Він дозволяє знаходити частинний розв. р-ня (1), якщо відома структура цього розв’язку, яка залежить від правої частини р-ня (1). Розглянемо ті випадки, коли метод невизначених коефіцієнтів може успішно застосовуватися для визначення частинних розв’ язків р-ня (1).

Теорема 1: якщо права частина р-ня (1) є добуток показникової функції на многочлен, тобто , де Р_п(х)-многочлен степеня ,то можливі наступні випадки:

а). число не є коренем характеристичного р-ня к² +рк+q=o. В цьому випадку частинний розв’язок слід шукати у вигляді

Підставивши значення в р-ня (1) і прирівнявши коефіцієнти при однакових степенях і одержимо систему (п+1) рівнянь з (п+1) невідомими з коефіцієнтами А₀, А₁, А₂,…,А_п;

б). число є простий (однократний) корінь характеристичного р-ня. В цьому випадку частинний розв’язок слід шукати у вигляді: ;

в). число є двократний корінь характеристичного р-ня: .

Теорема 2: якщо права частина диференціального р-ня (1) має вигляд де Р(х) і Q(x)- многочлени, то форма частинного розв’ язку визначається так:

а). якщо число не є коренем характеристичного р-ня, то слід шукати у вигляді: де U(x) i V(x)- многочлени, степінь яких дорівнює найвищому степеню многочленів P(x) i Q(x).

б). якщо число є коренем характеристичного р-ня , то частинний розв’язок слід шукати у формі: .

Зауважимо, що вказані форми а і б зберігаються і у випадку, коли один із многочленів P(x) або Q(x) дорівнюють 0, тобто права частина неоднорідного р-ня має вигляд або .

Теорема 3 (частинний випадок тереми 2): якщо права частина диференціального р-ня має вигляд , M, N-const

а). не є коренем характеристичного р-ня, то частинний розв’язок слід шукати: , А і В- деякі константи, які належить визначити.

б). якщо число є коренем характеристичного р-ня, то частинний розв’язок слід шукати у формі: , А і В-const, які необхідно визначити.

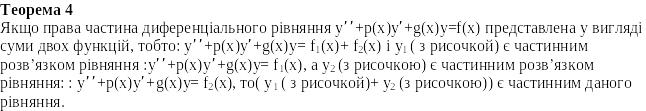
21.Числові ряди. Сума ряду. Збіжні і розбіжні ряди. Властивості збіжних рядів. Приклади.

Числовим рядом називають вираз виду а₁+а₂+а₃+….+а_п+..= (1), де а_п – числа, що належать певній системі. Для скороченого позначення рядів використовують знак суми .

Числа а_1, а₂, а₃,…,а_п,.. називаються членами ряду, а_п – загальний член ряду.

Приклади числових рядів:

а). із членів нескінченної геометричної прогресії можна скласти ряд

а₁+а₁q+а₁q²+a₁q³+….+a₁q^n-1+…=

б). ряд складається із чисел обернених натуральним числам

1+1/2+1/3+1/4+…+1/п+…= - гармонічний ряд.

Сума перших п-членів ряду назив. частинною сумою ряду і позначається .

Таким чином з рядом (1) пов’язана послідовність його частинних сум S₁, S₂, S_3,…., S_n,…, де S₁=a_1, S₂= a₁+a₂, S₃= a₁+a₂+a₃, S_n= a₁+a₂+a₃+…+a_n.

Ряд називається збіжним , якщо послідовність його частинних сум збігається, тобто існує скінченна границя . Число S називається сумою ряду. Якщо не існує або дорівнює , то ряд розбігається, розбіжний.

Приклад: дослідити на збіжність ряд ln2+ln3/2+ln4/3+ln5/4+…+ln(n+1/n)+…

S_n=ln2+ln3/2+ln4/3+ln5/4+…+ln(n+1/n)=ln(n+1).

- ряд розбіжний.

Розглянемо ряд нескінченної геометричної прогресії а₁+а₁q+а₁q²+a₁q³+….+a₁q^n-1+…

Сума перших п- членів або . Дослідимо ряд на збіжність в залежності від значення q:

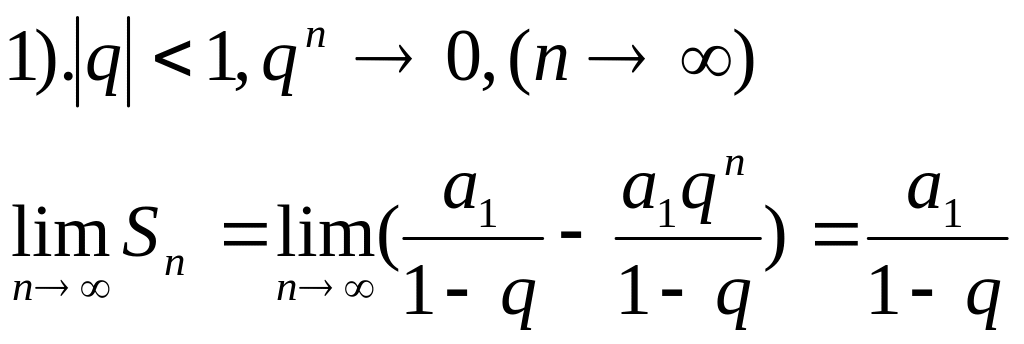
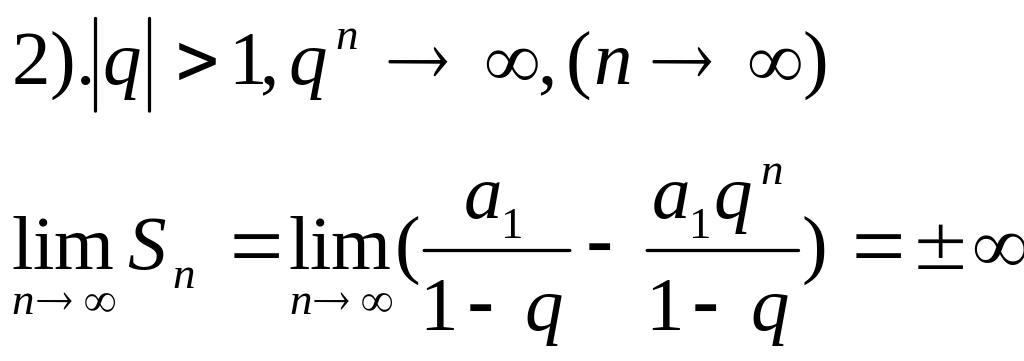
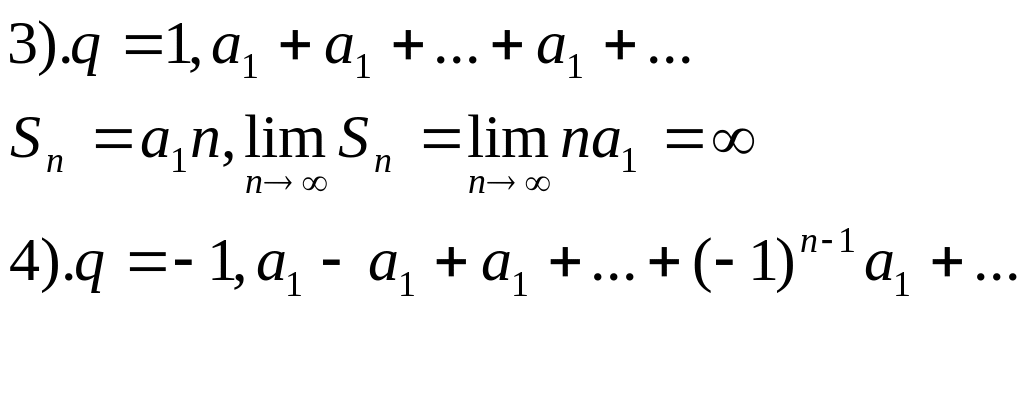lim S_n-не існує. Таким чином ряд при -збіжний, а при -розбіжний.

Властивості збіжних рядів.

Теорема 1: Якщо ряд збігається, який одержано із даного ряду відкиданням декількох його членів, то і збіжним є і сам ряд. І навпаки: якщо збігається даний ряд, то збігається і ряд, який одержано із даного відкиданням декількох членів. Іншими словами, на збіжність ряду не впливає відкидання скінченого числа членів. Теорема 2 : Якщо ряд а₁+а₂+а₃+а_n+… збігається і його сума = S_n, то ряд са₁+са₂+са₃+са_n+… збігається і його сума = с S_n. Теорема 3: Якщо ряди а₁+а₂+а₃+а_n+… і b₁+b₂+b₃+b_n+… -збігаються і їх суми S₁ і S₂ – відповідно, то ряди (а₁₊ b₁)+ (а₂₊ b₂)+…+( а_n+ b_n)+… і (а₁- b₁)+ (а₂- b₂)+…+( а_n- b_n)+… збігаються і їх суми = S₁+S₂ і S₁-S_2.

22. Необхідна ознака збіжності ряду. Гармонічний ряд. Якщо ряд а1+а2+а3+...+аn+... збігається, то його n-ий член ряду прямує до 0 при необмеженому зростанню n тобто,

lim an=0

n→∞ (1)

∞

∑

n=1 an збігається, то при n→∞ an→0

lim an=0

n→0

Якщо ряд збігається, то

Sn=a1+a2+…+an,

limSn=S (3)

n→∞

Sn-1=a1+a2+…+an-1,

lim Sn-1=S (3)

n→∞

від (2) – (3) одержимо

lim Sn-lim Sn-1=S-S=0

n→∞ n→∞

lim (Sn-Sn-1)=0

n→∞

Sn-Sn-1=an

lim an =0

n→∞

Зауваження:(1) Якщо n-ий член ряду прямує до 0, то ряд (1) може бути і розбіжним.

Зауваження:(2) Якщо n-ий член ряду не прямує до 0, то ряд є розбіжним.

Гармонічним називається ряд 1+1/2+1/3+...+1/n+…

Таку назву цей ряд має тому, що кожний його член, починаючи з другого , є середнім гармонічним двох його сусідніх членів зліва і справа.

Число С називається середнім гармонічним чисел a і b, якщо 1/С=1/2(1/а+1/b). Якщо С=1/n+1, a=1/n, b=1/n+2, то вказана рівність має місце для довільного n є N.

Гармонічний ряд розбіжний. Очевидно, Sn=1+1/2+1/3+…+1/n>∫ⁿ ₁dx/x.

Але ∫₁ⁿ dx/x=ln n →+∞, коли n →+∞. Тому limS_n = +∞. За означенням це і означає

n→∞

розбіжність рядду.

Узагальнений гармонічний ряд збіжний при α>1 і розбіжний при α≤1.