7.Екстремум ф-ї 2х змінних. Необхідна і достатня умови екстремуму.
Т. Мо(хо;уо) наз точкою локального max (min) ф-ї Z= f(х;у) в обл. Д , якщо для любої точчки М(х;у) із дельта околу т Мо(хо;уо) значення ф-ї в т Мо найбільше(найменше).
Точка Мо, в якій ф-я має екстремум наз точкою екстремуму. Max (min) значення ф-ї наз її екстремумом.
Необхідна умова існування екстремуму:
Я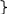
кщо
диференційована ф-яZ=
f(х;у) досягає екстремума в тчці Mо
(хо;уо)
то її частинні похідні 1-го порядку в
цій точці =0 або не існують.
∂z/∂x=0
∂z/∂у=0
Точки в яких частинні похідні = 0 або не існують наз критичними (стаціонарними).
Але не кожна стаціонарна точка є точкою екстремуму, а тому кожна стаціонарна точка повинна бути перевірена на екстремум за допомогою достатніх умов.
Достатні умови існування екстремуму.
I
Нехай функція
має неперервні частинні похідні до
другого порядку включно в деякій області,
що містить критичну точку
.
Тоді:
а)
якщо
в точці
,
то функція має в цій точці екстремум;
причому це буде мінімум, якщо
,
і максимум, якщо
;
б)
якщо
,
то екстремуму в цій точці немає;
в)
якщо
,
то потрібні додаткові дослідження,
оскільки екстремум може бути, а може й
не бути.
I
I
Нехай
– критична точка функції
.
Тоді, якщо за умови
,
другий диференціал
,
то в точці
функція
має максимум, якщо
,
то – мінімум, а якщо
змінює знак, тоді екстремуму в цій точці
немає.
8.Умовний екстремум ф-ї 2х змінних. Метод множників Лагранжа.
Нехай дано ф-ю Z=f(х;у) і L є Д. Потрібно знайти ext ф-ї Z=f(х;у) в точках , що належать L ліній.
Умовним ext ф-ї Z=f(х;у)наз екстремум цієї ф-ї, досягнутий при умові, що змінні х і у зв’язані рівнянням.У(х;у)=0 (рівняння зв’зку).
Z=f(х;у)
Уf(х;у)=0
Для знаходження точок ext використовують 2-а способи.
1)Поставлена задача зводиться до знаходження екстремуму ф-ї 1-ї змінної .Для цього треба розв’язати рівняння зв’язку відносно х або у і це значення підставити у ф-ю Z. у=у1(х) Z=f(х;у1(х))=f(х)—дослідити на ext.
2)Якщо із рівняння зв’язку складно знайти один із аргументів , то точки ext знаходять за методом множників Лагранжа.
Склад. Ф-я Лагранжа
L= f(х;у)+¡фі(ху), ¡—const.
Критичні точки визначаються із системи:
∂
L
/∂х=0
∂L /∂у=0
∂L /∂¡=0
9. Абсолютний екстремум (найбільше і найменше значення функції 2-ох змінних у замкнутій області)
Нехай задана функція z=f(x,y), яка визначена і диф. В області Д і досягає в області Д найбільше та найменше значення. Абсолютним екстремумм функції в області Д називається її найбільше або найменше значення в цій області. Функція може досягати абсолютного екстремуму аб в точці локальних min або max аб на межі області Д, тому щоб знайти найбільше і найменше значення функції в замкненій області треба:
1. Знайти критичні точки, що розташовані в області D та на її межі.
2. Обчислити значення функції в цих критичних точках.
4. З усіх знайдених значень вибрати найбільше і найменше значення.