40.Добуток подій. Залежні і незалежні події. Умовна ймовірність. Теореми множення для залежних і незалежних подій.

Добутком А*В подій А і В наз. Подія С яка полягає в тому що одночасно відбуваються обидві події і А і В.

Означення. Умовною ймовірністю Р(А/ В)(Р (А)) В називають ймовірність

події А, обчислену за умови, що подія В відбулася.

Теорема. Ймовірність добутку двох випадкових подій А і В дорівнює до-

бутку ймовірностей однієї із них на умовну ймовірність другої за умови,

що перша подія відбулася, тобто

Р(А · В) = Р(А) · Р(В / А) = Р(В) · Р(А / В).

Означення. Подія В називається незалежною від події А, якщо умовна

ймовірність події В за умови А дорівнює ймовірності В, тобто якщо P(B / A) =

= P(B) при P(A) ≠ 0. Якщо ж P(B / A) ≠ P(B), то подія В називається залеж-

ною від події А.

Теорема. Ймовірність добутку двох незалежних подій дорівнює добутку

їх ймовірностей.

P(A⋅ B) = P(A) ⋅ P(B). (1.11)

Доведення. Нехай А і В незалежні. За теоремою множення ймо-

вірностей P(A⋅ B) = P(A) ⋅ P(B/ A). Оскільки подія В не залежить від по-

дії А, то P(B / A) = P(B). Отже, P(AB) = P(A) ⋅ P(B).

Наслідок. Ймовірність добутку незалежних у сукупності скін-

ченної множини подій A (i 1,n) i = дорівнює добутку ймовірностей цих

подій.

P(A1*A2…An)=P(A1)*P(A2)…P(An).

41.Формула повної ймовірності.

Нехай подія А може наступити при умові появи однієї з несумісних подій які утворюють повну групу подій. Нехай відомі ймовірності цих подій і умовні ймовірності.

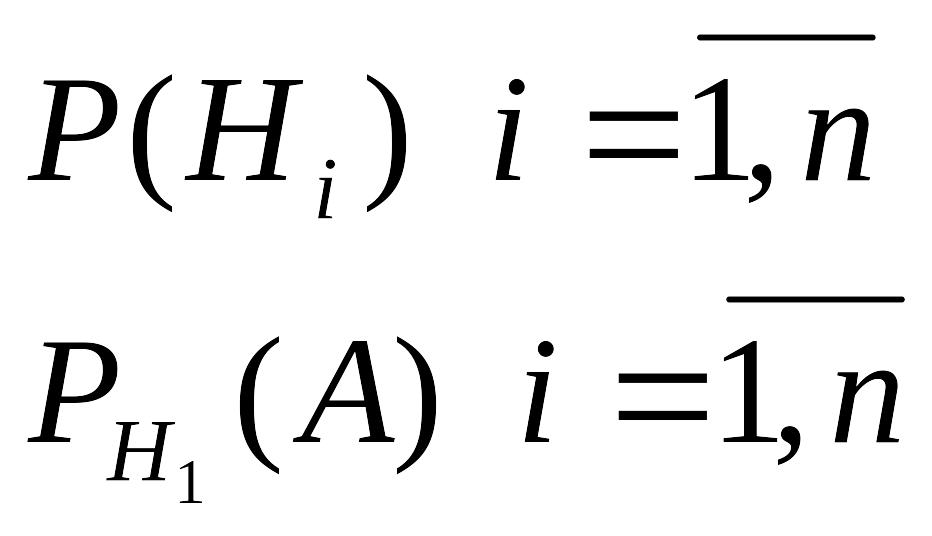
Необхідно знайти ймовірність події .

Теорема

Ймовірність події , яка може наступити лише при умові появи однієї з несумісних подій що утворюють повну групу подій дорівнює сумі добутків з цих подій на відповідному умовну ймовірностей події , тобто

-

Формула повної ймовірності

Доведення

Нехай подія може наступити тільки із однією із подій які утворюють повну групу подій, тобто може наступити

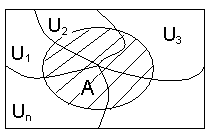
Із малюнка видно, що події є попарно несумісними, а тому попарно несумісними будуть і події .

Застосувавши до кожного доданку останньої рівності теорему множення ймовірностей одержимо:

42.Ймовірність гіпотез. Формула Бейєса.

Якщо подія А може настати тільки з однією з подій які утворюють повну групу попарно несумісних подій, то ймовірність події А обчислюється за формулою повної ймовірності

, (1.14)

де – ймовірність гіпотези

 – умовна ймовірність події А при цій гіпотезі,

З формулою повної ймовірності тісно пов’язана формула Байєса.

(1.15)

де .

Формула Байєса дозволяє переоцінити ймовірності гіпотез, прийнятих до випробування за результатами уже проведеного випробування.

43. Повторні незалежні випробування.Формула Бернуллі.

Нехай проводяться n випробувань, у кожному з яких подія А може як відбутись, так і не відбутись. Якщо ця ймовірність у кожному випробуванні не залежить від того, відбулась вона в інших випробуваннях чи ні, то такі випробування називаються незалежними щодо події А. Згідно з означенням випробування також незалежні, якщо в кожному з них імовірність настання події А однакова, тобто дорівнює тому самому числу. Імовірність того, що подія А відбудеться в кожному з незалежних випробувань, позначають а ймовірність настання протилежної події

Формула Бернуллі.

Імовірність того, що в n незалежних випробуваннях, у кожному з яких імовірність Р(А) = р, подія А відбудеться m раз, подається так:

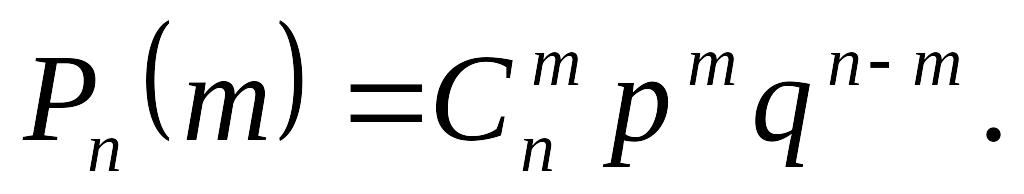Формула застосовується, якщо

Імовірність того, що в результаті n незалежних експериментів подія А з’явиться від mi до mj раз, обчислюється так: