Т.3. Теоремы и методы расчета сложных резистивных цепей

1.Основные определения

Узлом электрической цепи (схемы) называется точка, в которой сходятся не менее трех ветвей.

Ветвью электрической цепи (схемы) называется участок, состоящий из последова­тельно включенных элементов, расположенных между двумя смежными узлами.

Сложной называется электрическая цепь (схема), содержащая не менее двух узлов, не менее трех ветвей и не менее двух источников энергии в разных ветвях.

В сложной электрической цепи наблюдаются одновременно в той или иной мере раз­но­родные физические процессы, а именно, процесс генерирования электрической энергии, процесс преобразования электрической энергии в другие виды и процесс обмена энергией между магнитным полем, электрическим полем и источниками энергии. В общем случае для отобра­жения этих физических процессов схема замещения цепи должна содержать кроме источни­ков энергии (E, J) все разнородные схемные элементы (R, L, C). Математически фи­зические процессы в такой схеме можно описать системой дифференциальных уравнений, составлен­ных для схемы замещения по законам Кирхгофа.

В стационарном режиме (в режиме постоянного тока) напряжение на катушке равно нулю ( ), что соответствует короткому замыканию этого элемента, а при посто­янном напряжении ток в конденсаторе равен нулю ( ),что соответствует разрыву ветви с этим элементом. Следовательно, на установившийся режим постоянного тока схем­ные элементы L и C не оказывают влияния и могут быть исключены из схемы замещения (участки с L закорочены, а ветви с C удалены). Цепи постоянного тока представляются экви­валентными схемами, содержащими только по­стоянные источники энергии E, J и резистив­ные элементы R. Такие схемы получили назва­ние резистивных или постоянного тока. Уста­новившийся режим постоянного или перемен­ного тока в таких схемах описывается систе­мой линейных алгебраических уравнений, со­ставленных по законам Кирхгофа.

В настоящей главе будут рассматриваться только резистивные цепи в режиме посто­ян­ного тока. В последующем рассмотренные в данной главе теоремы и методы расчета бу­дут распространены на цепи переменного тока в установившемся синусоидальном режиме.

2.Метод преобразования (свертки) схемы.

Если схема электрической цепи содержит только один источник энергии (E или J), то пассивная часть схемы может быть преобразована (свернута) к одному эквивалентному эле­менту R_э ( рис.1 ).

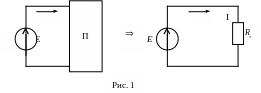
Свертка схемы начинается с самых удаленных от источника ветвей и проводится в не­сколько этапов до достижения полной свертки, после чего по закону Ома определяется ток источника . Токи в остальных элементах исходной схемы находятся в процессе об­ратной развертки схемы. Такой метод расчета токов получил название метода последова­тельного преобразования (свертки ) схемы.

При применении данного метода возможны следующие виды преобразований.

1)Последовательное преобразование заключается в замене нескольких элементов, включенных последовательно, одним эквивалентным (рис. 2 ).

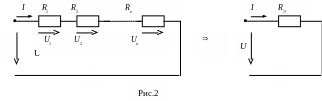
Несложно доказать, что справедливы следующие соотношения:

и

2)Параллельное преобразование состоит в замене нескольких элементов, вклю­чен­ных параллельно, одним эквивалентным (рис.3).

Несложно доказать, что справедливы следующие соотношения:

и

Для двух элементов: и

3)Взаимное преобразование схем звезда-треугольник (рис. 4) возникает при свертке сложных схем.

Условием эквивалентности двух схем являются равенства для них токов (I₁, I₂, I₃), на­пряжений (U₁₂, U₂₃, U₃₁) и входных сопротивлений (R₁₂, R₂₃, R₃₁) и соответственно входных проводимостей ( G₁₂, G₂₃, G₃₁).

Приравняем входные сопротивления для обеих схем со стороны двух произвольных ветвей при отключенной третей (рис. 4):

(1)

(2)

(3)

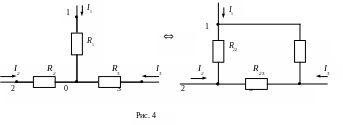
Сложим почленно уравнения (1) и (3) и вычтем уравнение (2), получим:

, аналогично получим , .

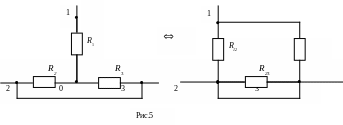
Приравняем входные проводимости для обеих схем со стороны произвольной вер­шины и двух других вершин, замкнутых накоротко (рис. 5):

(4)

(5)

(6)

Сложим почленно уравнения (4) и (5) и вычтем уравнение (6), получим:

, аналогично получим , .

В последних уравнениях заменим проводимости на соответствующие сопротивле­ния , получим:

; ; .

При наличии полной симметрии соотношение между параметрами эквивалентных схем составляет: .

4)Замена параллельных ветвей эквивалентной ветвью (рис. 6) осуществляется со­гласно теореме об эквивалентном генераторе.

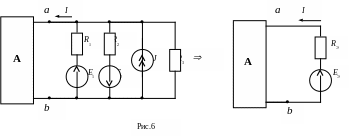
Напряжение холостого хода U_xxaв=E_Э — определяется по методу двух узлов:

.

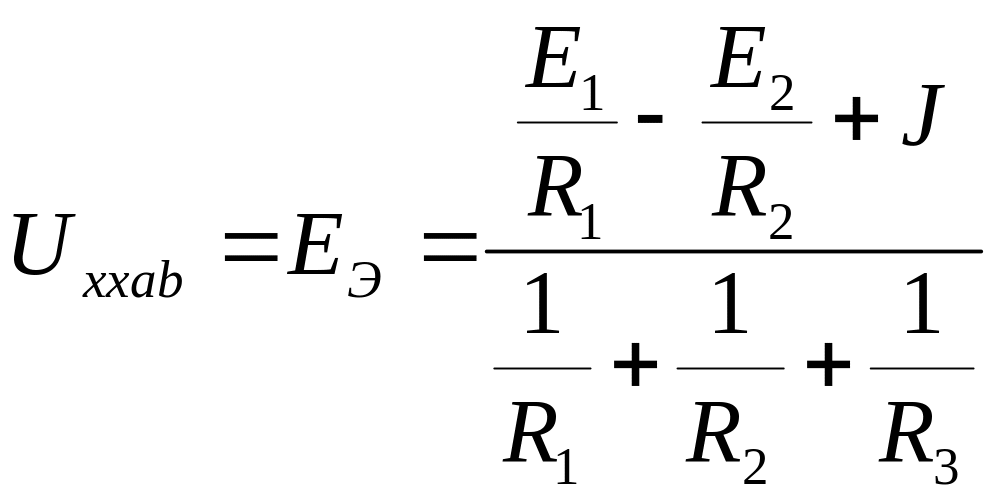Эквивалентное входное сопротивление находится методом свертки схемы:

.

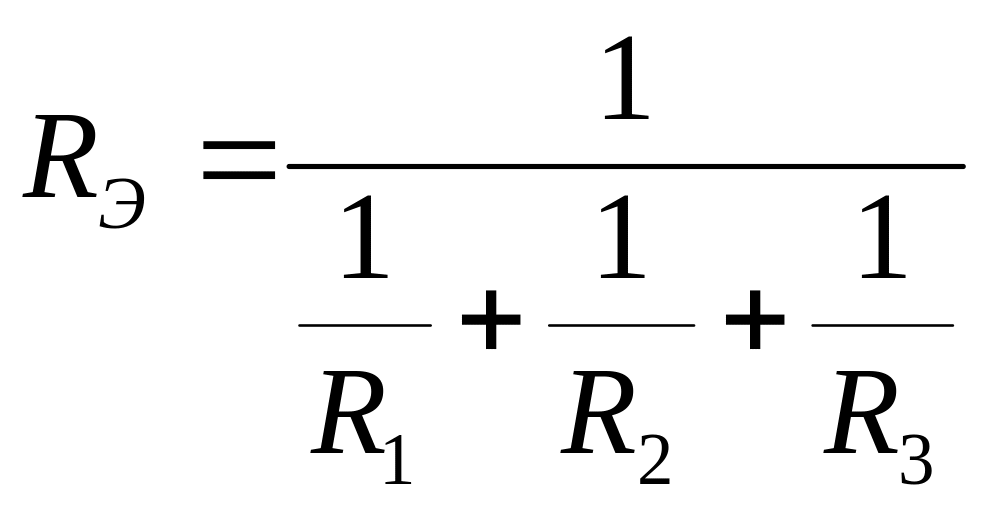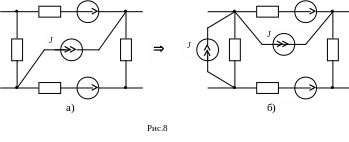
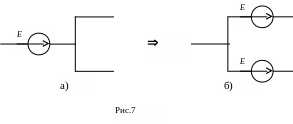
5)Перенос источника ЭДС через узел схемы: источник ЭДС Е можно перенести че­рез узел во все ветви, отходящие от узла (рис. 7а, б.).

6)Перенос источника тока согласно схеме (рис. 8а, б):