1. Уравнение дуги окружности в комплексной форме.

При изменении параметров одного из элементов сложной цепи токи всех ветвей, на­пряжения на всех элементах изменяются так, что концы векторов этих величин описывают дуги некоторых окружностей. Для исследования зависимости любой векторной величины (U, I) от переменного параметра достаточно определить дугу окружности, по которой пере­мещается конец этого вектора, другими словами, построить круговую диаграмму.

Уравнение дуги окружности в комплексной форме имеют вид:

,

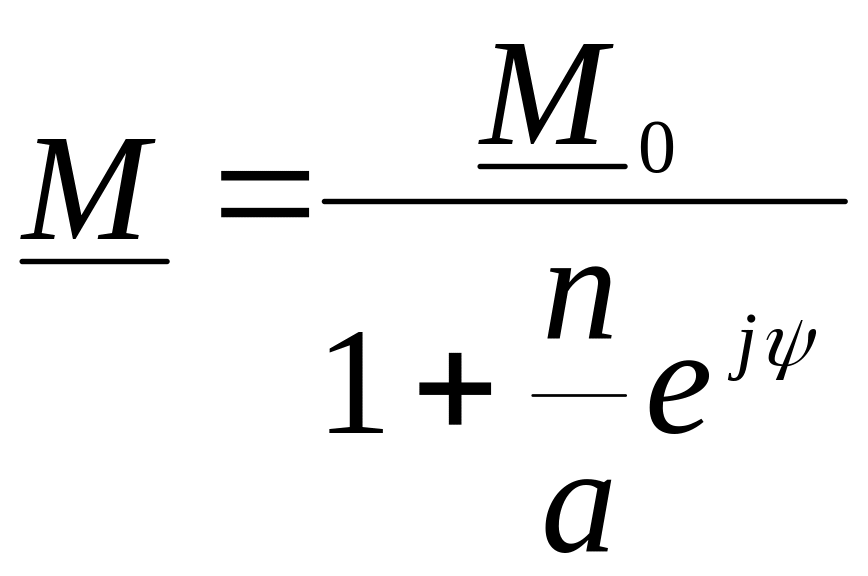где М = Мe^j – исследуемый вектор, M₀ - вектор-хорда дуги окружности, a = const – посто­янный коэффициент,  = const – постоянный угол, n = var = (0 - ) – переменный параметр.

Порядок построения круговой диаграммы по заданному уравнению:

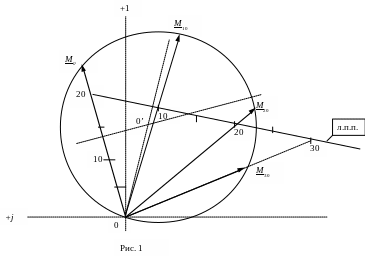
1. На комплексной плоскости в выбраном масштабе m_м откладывают вектор М₀=5e^j20 - хорду дуги окружности (рис. 1).

2. Вдоль вектора-хорды М₀ от его начала в выбраном масштабе m_а откладывают отрезок, равный коэффициенту “а”.

3. Из конца отрезка “а” под углом - к вектору М₀ проводят линию переменного параметра (л.п.п.), на которой нанаосят масштаб m_а, принятый ранее для отрезка “а”.

4. Определят положение центра дуги как точку пересечения двух перпендикуляров: первый проводят через середину вектора-хорды М₀, а второй – из начала координат к линии переменного параметра.

5. Проводят рабочую дугу по ту сторону от вектора-хорды М₀, где расположена линия переменного параметра.

6. Вдоль линии переменного параметра откладывают текущее значение параметра “n” соединяют точку с началом вектора М₀ (началом координат) и продолжают прямую линию до пересечения с дугой окружности. Искомый вектор М соответствует отрезку от начала координат до точки пересечения прямой линии с дугой окружности, при этом модуль вектора равен длине отрезка в масштабе m_м, а начальная фаза вектора – углу между вещественной осью +1 и напрвлением вектора.

На рис. 1 показано семейство векторов М, построенных для различных значений переменного параметра “n” (n= 0; 10; 20; 30).

2. Круговая диаграмма тока и напряжений для элементов последовательной цепи

Рассмотрим схему цепи, состоящую из последовательно включенных источника ЭДС E и пассивных элементов Z₁, и Z₂ (рис 2). Задано, что E = Ee^j=const, Z₁ = Z₁e^j1 = const, Z₂ = Z₂e^j2, где ₂=const, a Z₂ = var = 0÷ - переменный параметр.

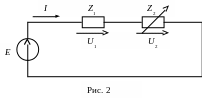
Преобразуем уравнение закона Ома для схемы к виду дуги окружности в комплексной форме:

,

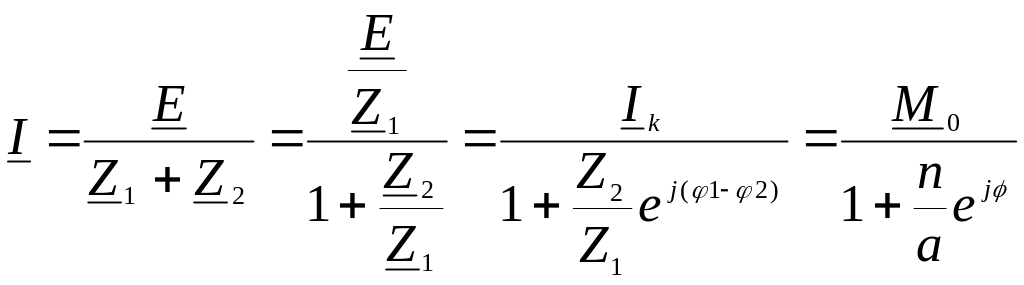где М₀ = I_к= E/Z₁ – ток короткого замыкания, соответствует вектору-хорде дуги окружно­сти, Z₂ = n = var – переменный параметр, Z₁= a = const - постоянный коэффициент, ₂ - ₁=  = const – постоянный угол.

Таким образом, уравнение для тока I является уравнением дуги окружности.

Напряжение на первом элементе представляет собой уравнение дуги окружности:

-

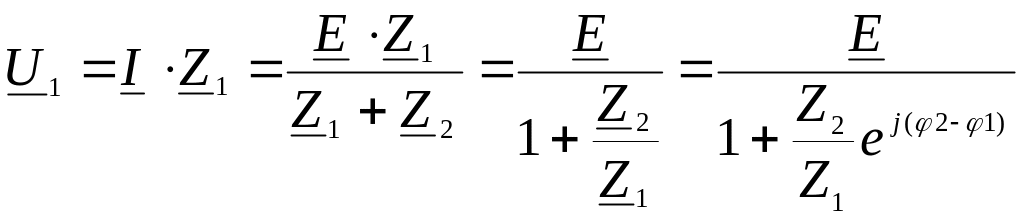Напряжение на втором элементе представляет собой уравнение дуги окружности:

-

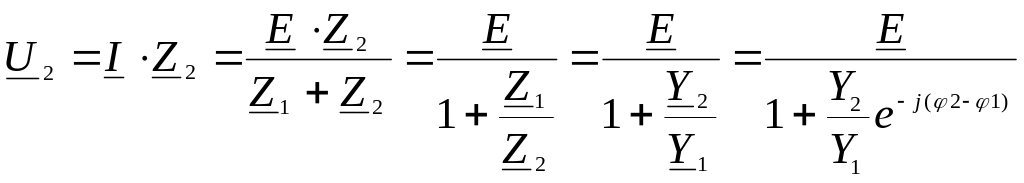Для каждого из векторов I, U₁, U₂ может быть построена круговая диаграмма со­гласно полученным уравнениям и по ним исследована их зависимость от переменного па­раметра n = Z₂.