Решение задач линейной алгебры на систолических массивах.

Систолические массивы появились в связи с ориентацией на специализацию при решении определенного класса задач.

Особенности систолических архитектур:

1. большое число функциональных устройств,

2. все функциональные устройства являются простым по организации и срабатывают за одно и тоже время,

3. входная и выходная информация соответствует друг другу (если информация на какой-либо систолический элемент не подается, то она должна обрабатываться внутри этого устройства),

4. конструктивно каждое функциональное устройство выполняется в виде четырех- или шестиугольника,

5. входы и выходы каждого систолического устройства выведены на границу многогранников.

Функциональные устройства, определенные таким образом называются систолическими ячейками. Из систолических ячеек можно складывать различные геометрические формы (мозаику), определенным образом соединяя эти элементарные ячейки друг с другом. Таким образом в результате получается специализированная вычислительная система, в которой все ячейки срабатывают синхронно по тактам. Такая система называется систолическим массивом. Основное ограничение – все систолические ячейки должны быть одинаковыми и располагаться водной плоскости (плоскостные массивы).

Пример.

A,B,C – двумерные ленточные матрицы.

Выполнить D=C+AB

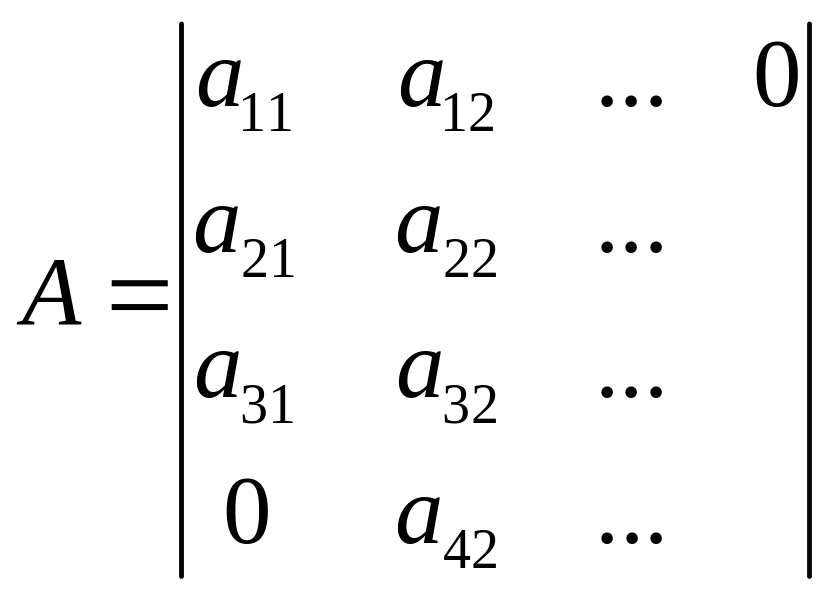
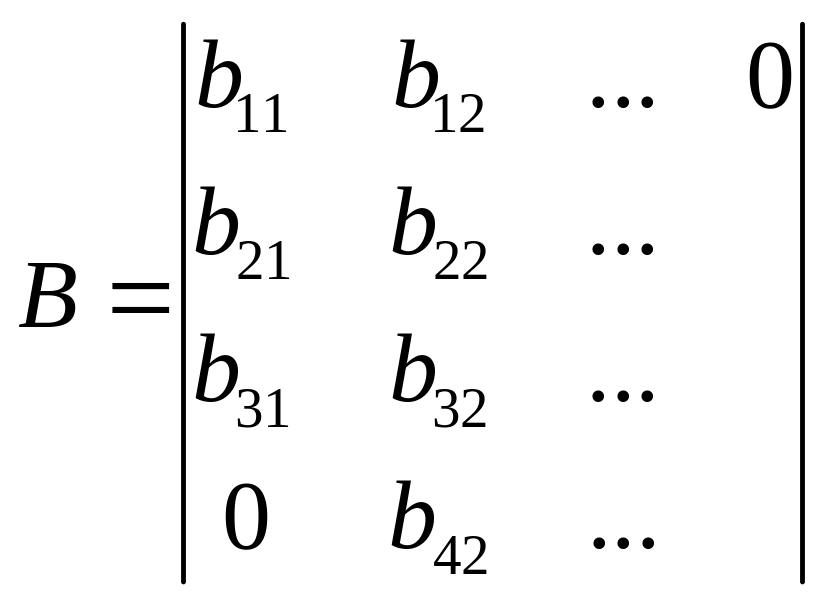
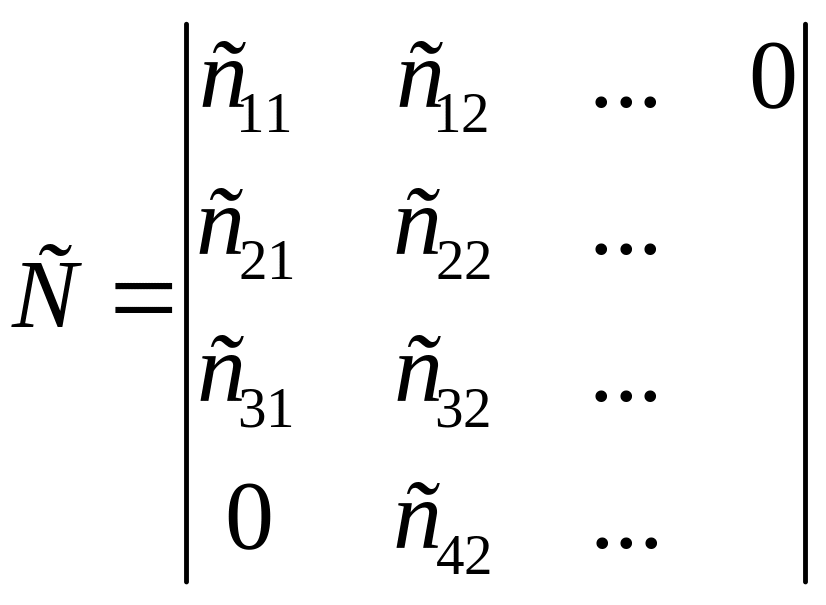
К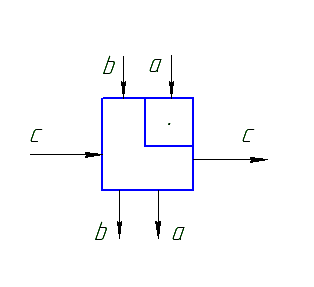 аждая ячейка может реализовать с+ab и осуществить одновременную передачу в следующую ячейку. Такая функциональность может быть реализована на четырех- или шестиугольной систолической ячейке.

И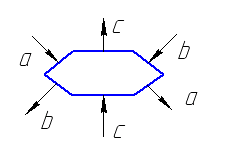 нформация перемещается по направлению стрелок. - без изменения передаются на выход в следующую систолическую ячейку. А над операндом с производится операция . Все операции выполняются по тактам. Передача информации в следующую ячейку осуществляется синхронно. Если в какой-то момент данные не поступили, то они заполняются нулями.

Вся плоскость на которой располагаются систолические ячейки покрыта косоугольной решеткой, которые определяют параллельные пути передачи информации.

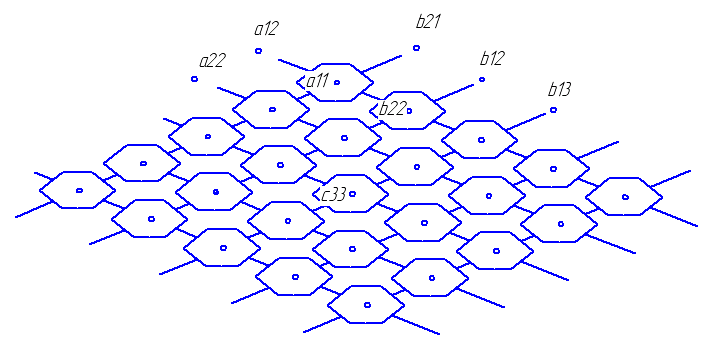
Основная задача, которая должна быть решена это расположение операндов в самих ячейках или на линиях связи этих ячеек таким образом, чтобы время подхода к систолической ячейке, в которой будет произведено действие было синхронизировано. Через каждый такт информация перемещается от ячейки к ячейке. В представленной схеме через каждые 3 такта будут выдаваться элементы матрицы D.

Существуют различные формы систолических массивов. Одни из наиболее распространенных форм реализации: решетка и куб.

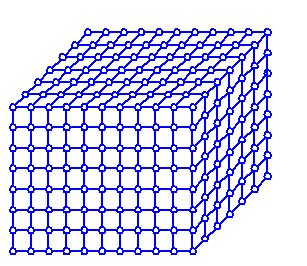
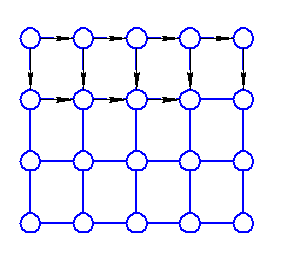
В зависимости от организации транспортной сети могут быть реализованы различные пути вычисления.

На основе исследований, проведенных с различными систолическими массивами, организуют алгебраические вычислители.

Схема алгебраического вычислителя.

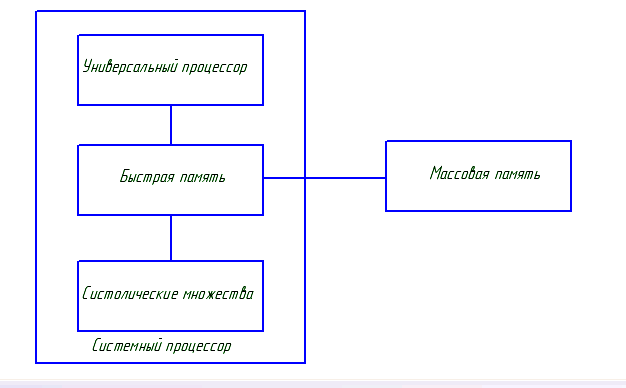
Преимущества:

• упрощаются алгоритмы вычислений

• снижается стоимость

• возрастает функциональность

Основной недостаток систолических массивов заключается в необходимости для каждого алгоритма формировать новую архитектуру, при этом возможно использование большого числа функциональных устройств, которые могут быть не полностью загружены, что снижает производительность системы.

Характеристики вычислительных алгоритмов позволяют наилучшим образом организовать архитектуру вычислительных систем для получения лучшего качества. С другой стороны исследование новых методов вычислительных систем позволяет создать лучшие алгоритмы.

22.1

Вычислительная поверхность «Meiko» для создания мультипроцессорной системы с заданными свойствами.

Анализ способов организации структур ВС привел к идее создания типовой вычислительной поверхности, которая была названа вычислительная поверхность Meiko – вычислительная среда, вычислительная среда, которая настраивается на решение определенных задач.

(Жесткая среда: дорого, не все модули будут действовать, следовательно, надо иметь набор модулей, конфигурацию осуществлять определенными способами (экспертная система и так далее)).

Meiko состоит из:

1. Набора типовых модулей, с помощью которых может создаваться любая структура

2. Интерфейсы этих модулей, которые позволяют этим модулям объединяться между

с обой, либо использовать стандартное оборудование.

3. Программное средство, с помощью

Которого может быть

распараллелен

Вычислительный

процесс, то есть должен быть

язык и транслятор, с

помощью которого

программу можно будет

автоматически распараллеливать

на однородные этапы.

Таким языком стал

Occam – 2:

описывает программы

с возможностью распараллеливания

на оборудовании. В качестве

вычислительных элементов используется

транспьютер. Общая схема вычислительного модуля (однородного,

который используется для построения схемы):

Каналы связи соединяют вычислительные модули в поверхность, что позволяет передавать сигналы. В поверхности можно использовать любую конфигурацию из тех, которые были рассмотрены выше.

При организации любой вычислительной поверхности:

Любая структура, создаваемая на основе вычислительных модулей должна отвечать требованию: время затрачиваемое на выполнение задач должно быть >> , чем время пересылки информации по сети. T_выч >> T_пер Иначе такая структура не имеет смысла. Производительность к стоимости должна быть максимальной.

Пример: n x n T_выч  n² (Умножение двух векторов размерности n x n); T_пер  3n² (ввод первого вектора, другого вектора …). Не имеет смысла.

Наиболее рациональная структура: Гиперкуб с диаметром n-1 и с числом узлов 2ⁿ позволяет в наибольшей степени соотнести между собой вычисления и пересылку информации.