Японская программа по развитию вычислительной техники:

1. (начало 70-х) направленная на то, что бы внедрить средства ВТ в как можно большее число заведений, особенно учебных. Стоимость одного часа машинного времени должна быть в 100-1000 раз меньше, чем в США. Следовательно: - можно больше времени уделять изучению ВТ; - повышать уровень подготовки специалистов – главная цель;

2. (конец 70-х) Создание СуперЭВМ, которые будут совместимы с аналогичными СуперЭВМ Европы и США. FACOM-VP 100 (Fujitsu) и Hitac, S.810 (Hitachi) совместимы с ICL (Англия) и IBM (США) (меньшие мощности, чем аналогичные образцы Запада). Сейчас, по тестированию TOP 500 первые 20 мест занимают японские машины.

Цель: использовать те алгоритмы, ПО, которые уже накоплены, т.е. воспользоваться опытом других стран и на этой основе создавать более мощные программы.

3. (начало 80-х) Создание японской СуперЭВМ в 100 раз большей производительности, чем аналогичные образцы Европы и США (более дешевы, чем аналогичные образцы Европы и США). Цель: завоевать рынок в области создания и использования ЭВМ

4. Создание ЭВМ 5-го поколения для решения задач, связанных с нечисловой обработкой информации (данные не в числовых функциях, а в символах, нечетких изображениях)

Отличие: машина должна сама найти алгоритм решения, составить программу и в соответствующей форме выдать результат. Основной язык: Prolog. Эта программа не была доведена до конца. Препятствие: необходимость создания огромной базы знаний, которая являлась бы основой для таких систем. Переориентация на создание интеллектуальных систем принятия решений в различных ситуациях.

5. (начало 90-х) RWCP (Real World Computer Program) Всемирная программа, связанная с разработкой высоких алгоритмов (простота, скорость, расходы памяти), т.е. эти алгоритмы должны быть не избыточными и обладал высокой скоростью.

Задачи:

1. Распознавание образцов (ситуаций, проблем и т.д.)

2. Обработка семантической информации, связанная с реализацией трансляторов с естественного языков. Приближает ВТ к человеку: не нужно перелагать язык специалиста на язык машины (не нужен промежуточный человек)

Существуют трансляторы с полуестетвенных языков

3. Управление роботами в любой среде (воде, воздухе и т.д. )

4. Задачи управления различными обменами, процессами и т.д.

Эти задачи выдвинуты в международном плане. Япония является координатором в этой области.

Машина 5-го поколения должна быть машина искуственного интелекта:

База

знаний

Вычислительная система 5-го поколения

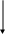
Внутренний формат

Преобразователь данных

языка

Естественный язык (Пролог)

Генератор программ

Язык Результат

Результат

Машина 4-го поколения

15.2 Способы распределения задач по процессорам в мультипроцессорных вс.

3. Процессоры в мультипроцессорной системе – однородные, то есть могут решать любые задачи из входного потока задач.

4. Процессоры в мультипроцессорной системе являются – специализированными (решают определенный тип задач)

Пусть имеется n процессоров и m задач. Необходимо так распределить m задач по n процессорам, чтобы общее время решения всех задач было минимальным. Наиболее известные алгоритмы такой задачи исходят из матричного программирования, в частности линейного программирования. Обозначим x_ij ситуацию, когда i-я задача решается на j-ом процессоре

Если x_ij = 1, то задача i решается на процессоре j. Если x_ij = 0, то иначе. П x_ij = 0 (1), где i = 1…n (так как задача решается на одном процессоре).  x_ij = 1 (2). t_ij – время решения i-ой задачи на j – ом процессоре.  x_ij t_ij = min (*)

Решить задачу, значит установить значения индексов i и j . Минимизировать (*). С учетом (1) и (2) составляется система из m линейных уравнений, решив которую найдем значение x_ij , при которых достигается min значения. Найдем, на каком процессоре какую задачу лучше выполнять.

П олучили распространение: Метод Шварца, метод Перт.

Метод Шварца, метод Перт.

Относятся к субоптимальным методам, при решении вводится гипотеза:

Минимизация решения на каждом из этапов (временных отрезков) приводит к минимизации всего решения в целом (оптимизация по шагам). К субоптимальным относится и метод динамического программирования.

Алгоритм распределения задач по методу Перт.

1. Процесс получения решения должен быть представлен в виде сетевого графика. 2. Сетевой график, или сеть, являются обобщением графа программы. 3. Граф представляется упорядоченной парой G = <E,D>. E – множество вершин графа. D – множество дуг, соединяющих вершины графа.

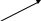
E = {1,2,3,4,5}

D = {1-1,1-2,1-3,1-4,3-2,3-5,4-5}

Д ля сети вводится понятие кортеж (включает большее число элементов чем пара)

S = <e ₀, e _t, E, D, A, F>

e ₀ – начальная вершина сети

e _t – конечная вершина сети (терминальная)

E – множество элементов

D – множество дуг, соединяющих вершины

A – множество весов, то есть каждая дуга должна быть “взвешена”. Это время, или количество операций, или объем памяти для записи передаваемой информации

F – функция, которая отображает веса на соответствующие дуги, то есть ставит определенный вес каждой дуге на графе вычислительного процесса.

F: A -> D

Пример:

e

2

₀ = 1

e

5

_t = 6

E

1

4

2

= {1,2,3,4,5,6}

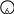
D = {1-2,1-3,1-4,2-5,3-5,4-5,5-6}

F

3

3

= {1-2(2),1-3(1),…}

С еть – ориентированный граф с исключением петель, отсутствуют обратные связи, так как процесс реализуется во времени. Задача: определить путь из вершины 1 в вершину 6 такой, чтобы сумма всех весов, соответствующих этому пути была минимальной. Найти последовательность выполнения вершин графа: t -> min

Какие ветки должны будут выполняться параллельно, чтобы t -> min (если все вершины были выполнены). Для реализации метода Перт вводятся понятия: самое раннее и самое позднее наступление события. t_(5) = t_2+t_2-5 = 7 – критический путь. t_(5) = t_1+t_1-2 . t_(5) = 6. t_(5)= 5

Для учета всех возможных вариантов реализации вычислительного процесса необходимо учесть наименьший путь выполнения процесса, то есть критический, наихудший путь. С учетом этого: Анализ сетевого графика необходимо начинать с конца, чтобы учесть критический путь. Начиная с терминальной вершины, выбираем вершину, которая является наихудшей и так далее для остальных вершин. При анализе двигаемся от терминальной вершины к начальной с определением наиболее эффективного пути.

П ример: Распределение задач в мультипроцессорной системе, состоящей из двух процессоров, на которых выполняются задачи определенного типа (специализированные). Исходные данные: сетевой граф с указанием последовательности выполнения работ и времени выполнения на каждом из процессоров.

I

0-1

1-4

6

II

I

3-4

2-4

1

5

4-5

II

I

1

5

II

5

2

3

3-5

II

I

1-2

4

II

2-3

1	Анализ начинаем с конца: анализируем вершину №5. Для этого определяем фронт работ (дуг графа), которые своими дугами заходят в вершину 5 4-5, 3-5 t4-5(5) = t(4)+5 = 16 t3-5(5) = 9+3 = 12 (выбираем max время)	1 шаг: I 4-5 II 0  = 5 (длительность выполнения работы)
2	Рассматриваем результаты, которые остались незавершенными на предыдущем шаге + работы, которые своими дугами заходят в вершину, для которой работа исходящей вершины завершена Для 4-ой: 1-4, 2-4, 3-4 будут рассмотрены только тогда, когда завершится 4-5. Входящие работы рассматриваются только тогда, когда выполнены исходящие работы 3-5, 1-4, 2-4, 3 – 4	2 шаг: I 2-4 II 3-4  = 2
3	3-5, 2-4, 1-4	3 шаг: I 2-4 II 0  = 3
4	3-5, 1-4	4 шаг: I 3-5 II 0  = 3
5	1-4, 2-3	5 шаг: I 1-4 II 2-3  = 4
6	1-2, 0-2, 1-4	6 шаг: I 1-4 II 0-2  = 2
7	1-2, 0-2	7 шаг: I 0 II 0-2  = 3
8	1-2	8 шаг: I 0 II 1-2  = 1
9		9 шаг: I 0-1 II 0  = 1

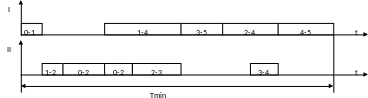
Анализируем и определяем момент, когда можно совмещать отдельные работы, причем рассматриваем наихудший (критический) путь

15.3