18) Простейшие движения твёрдого тела.
Поступательное движение: движение, при котором любая прямая, выбранная на этом теле, остаётся параллельна самой себе. AB||A’B’
Вращательное движение: движение твёрдого тела, при котором хотя бы 2 точки тела остаются неподвижными в процессе всего движения. Прямая, проход. Через эти точки, наз. Осью вращения.
ось вращения изображена связью типа: «цилиндрический шарнир».
19) Теоремы скоростей и ускорений точек тел при их плоском движении
Скорость любой точки плоской фигуры равна геометрической сумме скорости выбранного полюса и скорости точки во вращательном движении фигуры вокруг полюса.
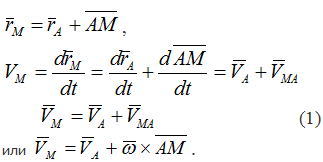
Ускорение любой точки тела при плоском движении равно геометрической сумме ускорения полюса и ускорения во вращении точки относительно полюса.
20) Угловая скорость и угловое ускорение.
Угловой скоростью называют векторную величину, характеризующую быстроту вращения твердого тела, определяемую как приращение угла поворота тела за промежуток времени.
Угловым ускорением называют степень изменения угловой скорости.
21)Равнопеременное вращение тела.
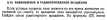
22) Скорость точки твёрдого тела, вращающегося вокруг неподвижной оси .
V=dS/dt=dφ⋅R/dt=ωR
V=ω⊗ r, V=ω⋅rsinα=ωR.
23) Ускорение точки твёрдого тела, вращающегося вокруг неподвижной оси .
24)Преобразования простейших движений твердых движений.
25)Плоскопараллельное (плоское) движение твердого тела.
Плоскопараллельным (или плоским) называется такое движение твердого тела, при котором все его точки перемещаются в плоскостях, параллельных некоторой неподвижной плоскости.
26)Теорема о сложении скоростей плоского движения.
27)Теорема о проекциях скоростей плоского движения.
28)Теорема о существовании мгновенного центра скоростей. Варианты его определия.
Любое непоступательное перемещение фигуры в плоскости можно осуществить поворотом вокруг некоторого неподвижного центра. В соответствии с этим легко доказывается, что при плоско-параллельном движении в каждый момент времени существует точка, неизменно связанная с плоской фигурой, скорость которой в этот момент равна нолю. Эту точку называют мгновенным центром скоростей (МЦС).
Методы определения МЦС:
