Силы и напряжения в ремне. Упругое скольжение ремня на шкивах

Возбуждение достаточных сил трения между ремнем и шкивами, обеспечивающих пе­редачу требуемого (заданного) момента, достигается путем предварительного (начального)

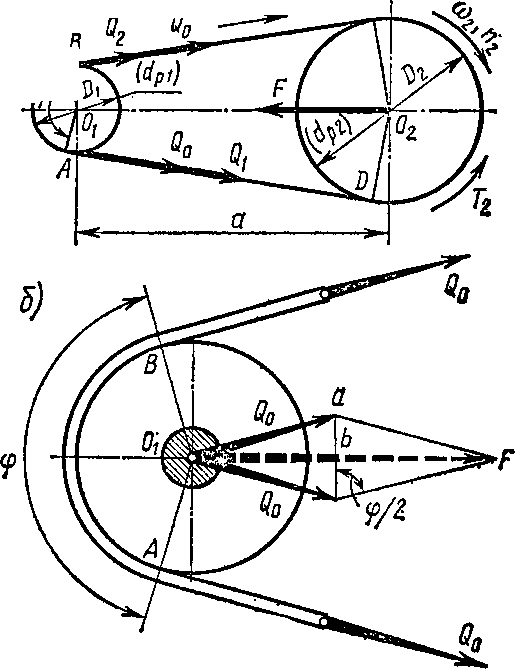
натяжения ремня; при этом в ветвях неработающего ремня воз­никает сила Q₀ (рис. 39). Такие же силы действуют и при холо­стом ходе передачи.

Напряжения растяжения от предварительного натяжения ремня

(38)

г де S —площадь поперечного сечения ремня, мм²; для плоских рем- ней .S = 66, где ъ — ширина и б —толщина ремня, принимаемые по табл. П5 ... П7; для клино- вых ремней- S = zS₀, где г—- q\ _ „ v с число ремней в передаче; S₀ — площадь поперечного vypr сечения одного ремня (сы.^'/фЛ табл. П8). Принимают сг₀ = = 1,57 ... 1,96 МПа для плоских ремней, сг₀ = = 1,18... 1,47 МПа для кли- новых ремней.

При работе ременной пе­редачи сила натяжения Q_t ведущей ветви ремня больше Q₀, а ведомой Q₂ — меньше (рис. 39, а).

Окружная сила ременной передачи

Из условия равновесия (при co^const) ведущего шкива (рис. 39, а)

=QA/2 - Q₂£>i/2 — 7\ = 0 получаем (Q_x — Q₂) DJ2 = Т_х и

Q₁-Q₂ = 2T₁/D₁

(а)

2^о =

Следовательно, окружная сила равна разности между силами натяжения ведущей и ведомой ветвей ремня.

Установим зависимость между Q_lf Q₂, Q₀ и Т⁷^

Так как геометрическая длина ремня не зависит от нагрузки, т. е. остается постоянной как в нагруженной, так и в ненагруженкой передаче, то для нагруженной передачи дополнительное растяже­ние ремня А/ (при возникновении в ведущей ветви ремня силы Q₀ + AQ) должно компенсироваться равным сокращением А/ Бедомой ветви ремня.

Итак,

Qi = Qo + AQ> Q₂ = Q₀-AQ.

Суммируя левые и правые части этих уравнений, получаем

Qi + Q₂ = 2Q₀. (б)

Из уравнений (а) и (б) получим формулы для вычисления Q_t и Q₂: Q_{1 =} Q₀ + 0,5F,; (39)

Q₂ = Q₀ — 0,5F_f. (40)

Отношение окружной силы к площади поперечного сечения

ремня —удельная окружная сила, условно называемая полезным напряжением:

a_P^F_f/S. (41)

Следовательно, напряжения а_х в ведущей и а₂ в ведомой ветвях ремня будут

а_г = QJS = (Q₀ + 0,5F_t)/S = а₀ + 0,5а^ (42)

а₂ = Q₂/S = (Q₀ - 0$F_t)/S = а₀ - 0,5а^. (43)

При огибании ремнем шкива в его поперечных сечениях возни­кают напряжения от центробежной силы

o_v = Q_v/S = _PSv*/S = p_mv* (44)

и от изгиба, которые достигают максимума при огибании ремнем малого шкива:

a_H = £6/D_min; (45)

где р_т — плотность ремня; Е—модуль упругости ремня при изгибе (см. табл. П2); б —толщина ремня.

Итак, наибольшее напряжение возникает в месте набегания ремня на малый шкив:

<W = <*о + 0,5о>+a_v + о_{и тах}. (46)

Наименьшее напряжение возникает в поперечных сечениях пря­молинейного участка ведомой ветви ремня:

tfmin = о о — 0,5a^+a_v. (47)

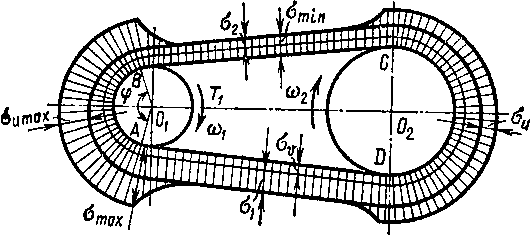
На рис. 40 показана эпюра суммарных напряжений, возникаю­щих в поперечных сечениях ремня при работе передачи. Так как удлинение ремня в точке А (рис 39,40) больше, чем в точке В, то за время t точка А шкива пройдет дугу АВ, а совпадающая с ней точка А ремня пройдет меньшую дугу вследствие сокращения его длины. Поэтому на участке дуги А В произойдет относительное изменение окружной скорости точки А ремня и шкива: скорость точки А шкива не изменится, а скорость точки А ремня начнет уменьшаться вследствие сокращения длины ремня, т. е. точка А ремня на дуге АВ отстает от движущейся точки А шкива и ремень на участке дуги АВ будет проскальзывать относительно соответст­вующих точек шкива —это и есть упругое скольжение.

Н а дуге CD ведомого шкива растяжение ремня от точки С к точке D увеличивается, а поэтому точка С ремня за время i пройдет больший путь, чем точка шкива, т. е. скорость точки С ремня больше, чем точки С шкива. Следовательно, на дуге CD происходит отставание то­чек шкива от движущих­ся точек ремня, т. е. так­же наблюдается упругое скольжение.

Итак, упругое сколь­жение является следствием неодинакового натяжения ремня в различных точ­ках по длине дуги обхва­та шкива.

Упругое скольжение является нормальным и закономерным явле­нием для любой ременной передачи. Оно существенно отличается от буксования, являющегося следствием перегрузки передачи.

Основные геометрические и кинематические соотношения в открытой передаче*. Усталостная долговечность ремней

Вследствие упругого скольжения окружная скорость v₂ ведомого шкива несколько меньше окружной скорости v_x ведущего:

где г—-коэффициент упругого скольжения:

₈ = (^—0,)/^ = 0,01 ... 0,02. (48)

Так как v_x = (d_lD_l/2 = v₂ = (o₂D₂/2 = nD₂n₂/60 и v₂=

=i>₁(l—e), то передаточное отношение (с учетом скольжения)

1^&₁/щ^п₁/п_Л⁹^0_ЛЦ0₁ (1—8)1. (49)

Наименьший угол обхвата (угол обхвата малого шкива) (см. рис. 39)

Ф а? 180° — [(D₂ — D_x)la\ 60°. (50)

Для плоскоременных передач рекомендуется ф^150°, а для клиноременных ф^120°. Если ф окажется меньше рекомендован­ных значений, то, необходимо увеличить межосевое расстояние а или установить натяжной ролик.

Длина ремня

^{L = 2а + {я 12) (D, + D2) + (D2 _Д)«/(4а). (51)}

* Для шкивов клиноременных передач вместо D и В следует принимать dp—расчетный диаметр шкива, М—ширину обода шкива (см. рис. 37 и табл. ГШ)

Для клиновых ремней найденное значение L необходимо согла­совать с табл. П8.

Межосевое расстояние а (при выбранном L) уточняется по фор­муле

а = {2L - п (D, + D₂) + V[2L - л (D, + D₂)f-8(D₂-(52)

При выполнении проектировочного расчета рекомендуется при­нимать:

для плоских ремней (D_t + £>₂)<а<2,5 (D^ + Dg);

для клиновых ремней 0,6(d_pf+ d_p2)<a< l,5(d_pl + d_p2).

Увеличение межосевого расстояния ведет к росту габаритов пере­дачи и повышению ее стоимости, а уменьшение —к снижению раз­мера угла обхвата и усталостной долговечности ремня.

Частота v пробега точки ремня в 1 с является одной из харак­теристик его усталостной долговечности.' Из многолетнего опыта эксплуатации ременных передач установлено, что для обеспечения приемлемой усталостной долговечности необходимо соблюдение не­равенств:

для плоских ремней

v = ^/L<4...5c-⁵, (53)

для клиновых ремней

v 10... 20с-'. (54)

Еще более ощутимо, чем частота пробега, на усталостную дол­говечность ремня влияет отношение 6/D_min. Для обеспечения тре­буемой усталостной долговечности эта величина в зависимости от материала ремня должна быть не ниже минимально допустимого значения (см. табл. П11).

Задача 8. Вычислить диаметр ведомого шкива плоскоременной передачи, угловую скорость и частоту вращения ведущего и ведомого валов, если диаметр ведущего шкива: a) £>i = 180 мм, б) £4 = 200 мм: передаточное отношение: a) i' = 3, б) / = 3.15; окружная скорость точки, находящейся на поверхности ведущего шкива: а) и =15 м/с, б) v = 20 м/с

Решение, а) 1. Диаметр ведомого шкива вычислим по формуле (49) при сред­нем значении коэффициента упругого скольжения е = 0,015:

£>2 = iDt (1 — 8) = 3.180 (1—0,015) = 532 мм.

По ГОСТ 17387—72 (см. табл. П10) принимаем £>₂ = 560 мм.

2. Определяем угловую скорость и частоту вращения ведущего вала (шкива):

®i = 2t;₁/D₁ = 2-15/0,18 = 167 рад/с; п₁=30©₁/я = 30-167/я=1600 мин"¹.

3. По формуле (49) уточняем передаточное отношение и определяем угловую скорость и частоту вращения ведомого вала (шкива):

t = D₂/[D₁(l— е)] = 560/[ 180(1— 0,015)1=3,15; 0)2 = 0)!// = 167/3,15 = 53 рад/с; п₂ = n_xli = 1600/3,15 = 507 ми н "¹.

Задача 9. Проверить усталостную долговечность клинового ремня, если* a) dpi = 200 мм, d_p2 = 500 MM, co_t = 150 рад/с, а = 800 мм; б) d_pi = 150MM, d_m~ = 400 мм, /г_х = 1460 мин^-*, я = 600 мм.

Решение, а) Усталостную долговечность ремня проверим по уравнению (54),

1. Определяем скорость ремня:

у==0,5М_р1 = 0,5.150'0,2 = 15 м/с . 2, По формуле (51) вычисляем длину ремня:

1 = 2а+0,5я (d_pi+d_p2) + (d_v2-d_vl)²/(4a) = = 2-0,8+ (я/2) (0,2+ 0,5)+ (0,5—0,2)?/(4.0,8) = 1,6+ 1,3 + 0,0281 3. По формуле (54) проверяем частоту пробега ремня: j v = v/L = 15/2,93 с-* = 5,12 c~*_f что меньше [v]_mi_n= 10 с^-1.

2,93 м.