Выбор основных параметров, расчетных коэффициентов и допускаемых напряжений

Модуль m закрытых цилиндрических прямозубых передач (для косозубых и шевронных — нормальный модуль т_п) определяют при известном межосевом расстоянии из соотношения

/я = /я„ = (0,01 ... 0,02)a_w (94)

и согласуют с СТ СЭВ 310—76 (см. табл. П23).

Зубчатые колеса с малыми модулями обеспечивают повышенную плавность хода передачи, так как при увеличении чисел зубьев сцепляющихся колес возрастает коэффициент перекрытия. Кроме того, в зубчатых передачах с малыми модулями уменьшаются потери на трение (меньше значения скольжения зуба в зацеплении); сни­жается расход материала (меньше наружный диаметр) и экономится станочное время при нарезании зубьев (меньше объем срезаемого материала).

Существенным недостатком мелкомодульных колес является зна­чительное повышение требований к точности и жесткости передачи вследствие концентрации нагрузки и особенно при перегрузках, когда возникает реальная опасность поломки зубьев. Поэтому в силовых передачах не рекомендуется применять т меньше 1,5., .2 мм.

Передаточное число одноступенчатой прямозубой цилиндрической передачи: и^12 в ручных передачах; и<7 в сравнительно мало­мощных и быстроходных передачах; и<4 в тяжелых передачах.

Число зубьев Zi и z₂ закрытой передачи при определенном из расчета a_w и выбранном т определяют по формулам (87), (86):

Zi = 2aj[m(u+l)] и г₂ = иг_г; z_±+z₂=zz.

Уменьшение т приводит к увеличению z_± и г₂, а следовательно, к повышению ряда качественных показателей передачи, однако прочность зубьев на изгиб понижается. Контактная выносливость зубьев при данном a_w от размера модуля не зависит.

П ри нарезании зубьев методом обкатки наименьшее число зубьев ограничивается их подрезанием, т. е. внедрением вершин зубьев ре­жущего инструмента (гребенки, дол-бяка) в тело ножки зуба. При на­резании зубьев методом обкатки

2mln=17 ^ПР^И условии отсутствия

подрезания, однако в передачах ре-дукторного типа (закрытых) по ука­занным выше соображениям стре­мятся иметь 2^20...30.

Предельная окружная скорость зубчатых колес в основном зависит от точности изготовления и монта­жа передачи (см. табл. П24). Коэффициент нагрузки

К_н=Kh$K_Hv и K_F = Kf$ K_Fv9

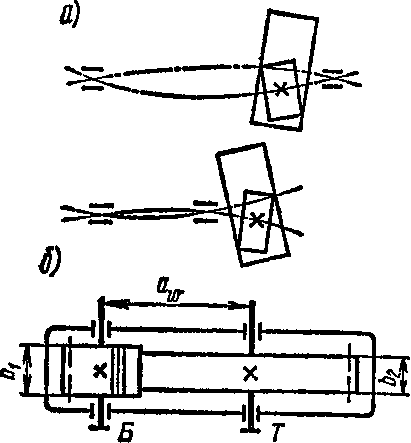
где /(яр и Kfp — коэффициенты, учитывающие неравномерность рас­пределения нагрузки по ширине венца при расчете на контактную и изгибную выносливость зубьев; принимаются по табл. П25. Не­равномерность распределения нагрузки по ширине венца колеса связана о деформированием зубчатых колес, валов и их опор, а также с погрешностями изготовления. При симметричном распо­ложении опор прогиб валов не вызывает перекоса зубчатых колес и, следовательно, почти не нарушает равномерность распределения нагрузки по длине зуба. При несимметричном и консольное рас­положении опор колеса перекашиваются (рис. 66, а), что приводит к нарушению правильного касания зубьев и распределения нагрузки по их длине. Влияние перекоса зубьев увеличивается с увеличением ширины колес, что приводит к ограничению значения %_d. Нерав­номерность распределения нагрузки увеличивает напряжение о_И и о_р у краев зубьев, что создает опасность выламывания углов зубьев. Применение колес со срезанными углами снижает эту опасность.

Для колес, изготовленных из прирабатывающихся материалов НВ350), неравномерность нагрузки постепенно уменьшается вследствие повышенного местного износа. Применение жестких валов, опор, корпусов и нешироких зубчатых колес способствует снижению неравномерности нагрузки и, следовательно, уменьшению значений

K _Hv ^и /С/^ —коэффициенты, учитывающие динамическую нагрузку, возникающую в зацеплении,—определяют по табл. П26 в зависи­мости от степени точности (см. табл. 2), окружной скорости и твер­дости зубьев колеса z₂ передачи. Основное влияние на увеличение значений K_Hv ^и %fv ^име" ют ошибки основного ша­га р_ь, погрешности наре­зания зубьев, окружная скорость, упругость зубь­ев и др. Например, при Pb2 > Ры вторая пара зубьев вступает в зацеп­ление до выхода на ли­нию зацепления, что при­водит к мгновенному изменению значения пере­даточного числа и кромоч­ному удару. Для умень­шения эффекта кромочно­го удара, увеличивающего

динамическую нагрузку и вызывающего задир поверхности зубьев, применяют фланкирование зубьев —верхний участок эвольвенты выполняют с отклонением в тело зуба.

Коэффициенты ширины зубчатого колеса %_а и Рекоменду­емые значения %_a = b/a_w для быстроходной ступени цилиндрического многоступенчатого редуктора при симметричном расположении зуб­чатых колес относительно опор (рис. 66,6) %_а = 0,315.. .0,5, при" несимметричном (рис. 67) %_а = 0,25.. .0,4 и консольном располо­жении одного или обоих колесу=0,2.. .0,25. Меньшие значения %_а принимают для передач с повышенной твердостью рабочих поверх­ностей зубьев (> HRC45). Для каждой последующей ступени пере­дачи редуктора ty_ba увеличивают на 20...30%. Для передвижных зубчатых колес коробок передач ty_ba = 0,1.. .0,2.

Отношение ширины венца к начальному (делительному) диаметру шестерни %_d = b/di рекомендуется принимать при ^СНВ350 в зави­симости от степени точности изготовления: %_d = 1... 1,5 при 6-, 7-й степенях точности, i|>_w = 0,75...1 при 8-й и t|)_w<0,75 при 9-й и 10-й.

Нормы (степень) точности выбирают в зависимости от назначе­ния, условий работы и окружной скорости передачи (табл. 2).

При твердости рабочих поверхностей зубьев > HRC45 значения %d следует принимать на 20...30% меньше указанных для твер­дости ^ НВ350. При консольном расположении 1^ = 0,5.. .0,8. Для

к

Таблица 2. Степень точности по нормам плавности цилиндрических (СТ СЭВ 641—77), конических (СТ СЭВ 186—75) и червячных (СТ СЭВ 311—76) передач в зависимости от скорости

Степень точности передачи	Окружная скорость и, vm\ скорость скольжения v$, передачи, м/с
	цилиндрической		конической	червячной
	прямозубой	непрямозубой	прямозубой
6-я—высокоточные пере-	< 15	<30	<12	<15
дачи
7-я—точные	» 10	» 15	» 8	» 10
8-я—средней точности	» 6	» 10	» 4	» 5
9-я—пониженной точности	» 2	» 4	» 1,5	» 2

оробок передач ty_bd = 0,15.. .0,4. Для открытых передач = = (10... 12)/^.

С увеличением ty_ba и ty_w уменьшаются масса и габариты пере­дачи, однако увеличение ширины венца Ь колеса снижает точность контакта зубьев по их длине. Выбор значений %_d определяет качество работы передачи, ее КПД, габариты и требования к тех­нологии изготовления, точности монтажа и жесткости конструкции. Следовательно, физическая и техническая сущность if_w зубча­тых колес аналогична я|) фрикционных катков (см. занятие 2). Кроме того, с увеличением ty_bd повышается концентрация нагрузки.

Между коэффициентами %_а и %_d существует зависимость

Фм = 0,5ф_6в(а± 1).

Коэффициент, учитывающий механические свойства материалов сопряженных зубчатых колес,

^Zm== Уn(l-v²) ⁼ ]^//Гп(\^)(Е₁+Е₂) №)

принимают по табл. П22, E_t и £₂ — по табл. П2.

Коэффициент, учитывающий форму сопряженных поверхностей зубьев,

Z_//=|/^r2/sin2a. (96)

При а = 20° г_я=1,76.

Коэффициент Z_e, учитывающий суммарную длину контактных линий,

Z₈ = ]/(4-e_a)/3. (96а)

Коэффициент торцового перекрытия

е_а« [1,88-3,2 (l/z_t± 1/г_я)]совр. (97)

Для прямозубых передач р = 0.

Коэффициент формы зуба Y_р принимают по табл. П27 в зави­симости от числа зубьев г.

Проверочный расчет по формуле (92) и проектировочный по фор­муле (93) необходимо выполнять по более слабому элементу (шес­терни или колесу), у которого значение a_FP/Y_F меньше.

Допускаемое контактное напряжение (МПа) определяется по за­висимости

*нр = <ЪрКнь (98)

где aj/p—допускаемое контактное напряжение, МПа, соответствую­щее базе испытаний N_m (см. табл. П28). Коэффициент циклической долговечности

K_HL=VN_H0/N_HS. (99)

Здесь N_H0 — база испытаний напряжений, соответствующая дли­тельному пределу выносливости (см. табл. П28); jV^—относитель­ное эквивалентное число циклов напряжения [см. формулу (100)].

В зубчатой передаче число циклов напряжений обычно связано с частотой вращения п (мин*¹). Тогда при постоянной нагрузке и зацеплении с одним колесом

Nhe = N*_FB = N% = 60/_qn, (100)

где f₄ — ресурс передачи, т. е. суммарное число часов ее работы за расчетный срок службы (наработка передачи в часах).

Если полученное значение N_HE>N_m, то принимают N_HE=N_H0 и /С/иг = 1. При малом сроке службы передачи /С_Я£^>1 и допускае­мые контактные напряжения по циклической выносливости могут оказаться больше, чем по статической прочности. Поэтому предель­ное значение K_hl ограничивают: для стальных колес при однород­ной структуре материала зуба /C//l^2,6, при поверхностном упроч­нении /С_я1<1,8; для чугунных колес \<^К_Нь^Л\ для неметал­лических /Сял= 1.

Допускаемое напряжение a_FP при расчете на выносливость зубьев при изгибе, соответствующее базе испытаний напряжений, опреде­ляют по зависимости

o_FP = ofoK_FL, О⁰¹)

где o°_Fp—допускаемое напряжение при расчете на выносливость зубьев при изгибе, МПа, соответствующее базе испытаний напря­жений N_Fo. Значения g_fp для работы одной стороной зуба (нере­версивные передачи) и двумя сторонами (реверсивные) приведены в табл. П28. Коэффициент циклической долговечности

^mV^fo/N_FE. (102)

* При ступенчатой циклограмме нагружения (переменный режим) N_HF, N_FB определяются по зависимости, приведенной в ГОСТ 21354—75.

Для стальных зубчатых колес с нешлифованной переходной по­верхностью при твердости поверхности зубьев > НВ350 и чугунных

4 № 2484

97

колес m_F=9. Для стальных зубчатых колес с твердостью поверх-ности зубьев < НВ350, а также колес, закаленных ТВЧ, с обры­вом закаленного слоя у переходной поверхности или колес со шли­фованной переходной поверхностью независимо от твердости и термообработки зубьев m_F=6.

Число циклов напряжений при постоянной нагрузке определяют по формуле (100). При N_FE^N_F0 принимают K_FL=l. Чтобы при действии расчетной нагрузки не произошло разрушение зуба от нарушения статической прочности, максимальные значения коэффи­циента K_Fl ограничивают: при m_F=9 /С/^^1,63, при т_/7==6 /С«<2,08.

Особенности расчета открытых цилиндрических передач. В от­крытых передачах перед определением модуля задаются значением г_г\ обычно принимают Zi=17...22, но в отдельных случаях (чаще з ручных передачах) г± снижают до 15 и даже 12 зубьев, т. е. до­пускают работу зубьев, имеющих ослабленную (подрезанную) ножку.

Открытые передачи обычно выполняют только прямозубыми и применяют при и^З м/с. Степень точности их изготовления по нормам плавности контакта СТ СЭВ 641—77 обычно 9-я.

Основные размеры определяют из расчета на изгибную проч­ность зубьев. При расчете принимают допускаемые напряжения o_FP = o°_Fp и о_нр = о°_НР, т. е. без учета коэффициента циклической долговечности K_HL = K_FL = 1. Коэффициенты Kh_v = Кр* = ^ При любой твердости рабочих поверхностей зубьев открытые передачи считаются прирабатывающимися.

В открытых передачах расчетное значение модуля (93) обычно принимают в 1,5... 2 раза больше, чем в закрытых передачах рав­ной мощности.

Задача 18. Вычислить основные параметры зацепления прямозубой цилинд­рической передачи, если: а) т = 3 мм, и = 4, z₂ = 80; б) Zx = 22, z₂=6G, di — 88 мм.

Решение, а) 1, Зная и и г₂, по формуле (86) определяем число зубьев шес­терни:

г_х,= г₂/ы = 80/4 = 20.

2. Находим высоту головки и ножки зубьев шестерни и колеса (см, заня- тие 8):

h_a = m = 3 мм, /^=1,25/72= 1,25-3 = 3,75 мм.

Высота зуба /i = ft_tf+/i/=3 + 3,75 = 6,75 мм.

3. По формуле (83) определяем делительный диаметр: шестерни c(₁ = mz₁ = 3-20 = 60 мм,

колеса = mz₂ = 3• 80 = 240 мм.

4. По формуле (84) вычисляем диаметры вершин зубьев: шестерни d_ai = d₁ + 2m = 60+2.3 = 66 мм,

колеса d_a2 = d₂ +2m = 240+2-3 = 246 мм.

54. По формуле (85) находим диаметры впадин: шестерни d/_x = ^—2,5/^ = 60—2,5-3 = 52,5 мм, колеса dfl, = d₂ — 2,5m = 240—2,5-3 = 232,5 мм.

55. Межосевое расстояние определяем по формуле (87):

aw = 0/2) (d_t+ d₂) = (I /2) (60+240) = 150 мм.

Задача 19. Непосредственным измерением найден диаметр вершин зубьев прямозубого цилиндрического колеса: a) d_a = 200 мм, б) d_a = 400 мм.

Вычислить остальные параметры зубчатого колеса, если подсчитано, что число зубьев колеса: a) z = 98, б) г = 48.

Решение, а) 1. По формуле (84) определяем модуль:

d_a = d-\-2m = mz-\-2т — т (z+2)

и

m = d_e/(z + 2) =200/(98 +2) = 2 мм,

2. По формуле (83) вычисляем делительный диаметр:

d = _mz = 2-98 = 196 мм.

3. Диаметр впадин зубчатого колеса найдем по формуле (85):

6^ = 6?—2,5т= 196—2,5-2= 191 мм.

Задача 20. Вычислить силы, действующие в зацеплении прямозубой цилинд­рической передачи, если: а) Р=20 кВт, v — З м/с; б) Р = 14 кВт, v = 2,5 м/с Решение, а) 1. Определяем окружную силу:

^ = р/_у==20.10³/3 = 6,67.10³ Н = 6,67 кН.

2. По формуле (89) находим радиальную (распорную) силу:

F_r = F_t tga=F/tg20° = 6,67.0,364 = 2.43 кН.

Занятие 9. МЕТОДИКА РАСЧЕТА ЗАКРЫТЫХ И ОТКРЫТЫХ ПРЯМОЗУБЫХ ЦИЛИНДРИЧЕСКИХ ПЕРЕДАЧ

При проектировочном расчете зубчатой передачи обычно мощ­ность и угловая скорость (частота вращения) на валу зубчатого колеса известны. Конечно, мощность и угловая скорость могут быть заданы на ведомом валу. Тогда придется примерно оценить КПД передачи, найти требуемую мощность электродвигателя и подобрать электродвигатель мощностью не ниже требуемой, но по возможно­сти близкой к ней и с такой угловой скоростью, чтобы передаточ­ное отношение проектируемой передачи было в заданных пределах. Кроме того, обычно бывают заданы режим работы и срок службы проектируемой передачи.

Рекомендуется следующий порядок расчета передачи.

56. Определить передаточное отношение.

57. Найти вращающий момент на валу шестерни.

58. Выбрать материалы для изготовления шестерни и колеса, назначить режим работы (реверсивная, нереверсивная; нагрузка постоянная или переменная), срок службы передачи и найти до­пускаемые напряжения (контактные и изгиба).

59. Предварительно задаться значениями коэффициента ширины¹ колес %_а или ^_bd (см. занятие 8) и найти Кн$ или Kf$ (см. табл. П25).

60. Для закрытой передачи определить межосевое расстояние a_w9 а для открытой или закрытой с высокой твердостью зубьев — модуль т.

6. Вычислить параметры передачи.

7. Уточнить межосевое расстояние и определить ширину колес (ширину шестерни ъ_х рекомендуется принимать на 2.. .5 Мм больше

4*

99

ширины зубчатого колеса 6₂ —учитывается неточность сборки и возможная осевая «игра» передачи). Необходимо, чтобы b_t и Ь₂ были выражены целыми числами (мм).

8. Вычислить окружную скорость и назначить соответствующую степень точности передачи (см. табл. 2).

9. Уточнить значение коэффициента нагрузки К_н и K_F.

10. Вычислить силы, действующие в зацеплении.

11. Проверить расчетные напряжения [см. формулы (90), (92)] и в случае их отличия от допускаемых изменить параметры пере- дачи (m, a_w) или термообработку.

Если расчетные напряжения о_н и а_Р меньше допускаемых, то расчет можно считать законченным. Нет необходимости в пере­счете, если превышение расчетных напряжений над допускаемыми в пределах 5%.

Следует учесть, что при проверке на изгиб зубьев (с твер­достью <НВ350) закрытой передачи, размеры которой определены из расчета на контактную выносливость, обычно оказывается, что расчетные напряжения изгиба значительно ниже допускаемых. Этот результат не должен рассматриваться как недогрузка передачи и ее параметры изменять не следует.

Обычно открытые передачи на контактную выносливость не про­веряют. Однако в целях устранения опасности заедания (при твер­дости зубьев < НВ350) рекомендуется и открытые передачи про­верять на контактную выносливость зубьев.

Задача 21. Рассчитать открытую и закрытую (см. рис. 63, а и 66) цилиндри­ческие прямозубые нереверсивные передачи, если: а) Р_г = 18,5 кВт, п_х = 735 мин"¹, п₂ = 210 мин-¹; б) Pj = 45 кВт, /1_х = 980 мин"¹, п₂ = 245 мин"¹.

Материал зубчатых колес: а) сталь—сталь; б) сталь—чугун. Нагрузка с умеренными толчками.

Решение, а) 1. По формуле (16) определяем передаточное отношение, равное и [см. (86)]:

i = т/п₂ = 735/210 = 3,5 = и.

2. Находим вращающий момент на валу шестерни:

Т_х = 9.55РХ/Л! = 9,55-(18,5-10³/735) = 240 Н• м.

3. Выбираем марку материала и назначаем химико-термическую обработку зубьев; определяем допускаемые напряжения.

Используя табл. П21 и П28, назначаем для изготовления зубчатых колес сталь 45 с поверхностной закалкой ТВЧ до твердости > НВ350.

Допускаемые напряжения на контактную и изгибную выносливость зубьев вычисляем по формулам (38) и (101).

Принимая по табл. П28 для стали 45 (HRC40.. .52) 0^ = 800 МПа, ^яо = 6-Ю⁷; o⁽j_?p=230 Mljla для нереверсивной передачи, N _Fo — 4-10^е и назначая ресурс передачи *_ч = 10⁴ ч, по формуле (100) находим число циклов напряжений: N_HE=N _FE=60t₄n₂ = 60-10⁴.210 = 12,6-10⁷.

Так как Nhe> Mho и N_fe > N_Fo, то значение коэффициента циклической долговечности [см. формулы (99, 102)] /C/fi = l ^и K_Fi-\ (см. занятие 8). Итлк, допускаемые напряжения:

fftfP^o^ptftfL = 800-1=800 МПа; o_FP = о»_pK_fl = 230• 1 = 230 МПа.

4. Выбираем коэффициенты, входящие в формулы (91) и (94).

По табл. П22 для прямозубых колес tf_a=4950 Па¹/³ для материала сталь-, сталь.

Коэффициент ширины зубчатых колес %_д = 0,315.. .0,5 при симметричном расположении зубчатых колес относительно опор (см. занятие 8). Принимая г|?&д=0,4, определяем г|?&<* по формуле на с. 96: г|>_м=0,5%_{д К}и+1) =0,5-0,4 (3,5+ 1) =0,9.

По табл. П25, интерполируя, находим (при > НВ350) tf//e = l,08 и /Cfp= 1,П5.

5. По формуле (91) вычисляем межосевое расстояние закрытой передачи:

= 22,3-10³ j/289-Ю-¹⁸ = 147,5-10~³ м=147,5 мм. Принимаем a_w — \50 мм.

6. Для вычисления модуля открытой передачи [см. (93)] необходимо найти Zi, z₂, Yf ^и наименьшее значение прочностной характеристики o_FP/Y_F зуба. Принимая Zi = 20 по формуле (86), определяем число зубьев колеса:

22=^^ = 3,5-20 = 70.

По табл. П27 находим Y_F при г_х = 20 и z₂ = 70: У£. = 4,12, Y"_F = 3,815— сред­нее значение при z = 60 и z = 80.

Так как Y'_F > Y"_F, a o_FP принято общим для шестерни и колеса, то o_FPJY_F (см. занятие 8) _удля шестерни будет меньше, чем для колеса и, следовательно, расчет на прочность зуба при изгибе необходимо выполнить по зубу шестерни. Итак, модуль передачи (93) при /(_w = l,4

mi

\ /Y'_FW_X » /4,12-1,115-2j0 8/ ₀...

^КяУ фъ*°рр *У 20^.0,9.230.10«-^1>4|/13'^3,10 ■

= 3,16-10~³ м.

По СТ СЭВ 310—76 (см. табл. П23) принимаем т = 3,5 мм.

7. Определяем параметры передачи.

Для закрытой передачи по формуле (94) находим модуль:

т = (0,01.. .0,02) a_w = (0,01.. .0,02) 150 = 1,5.. .3,0 мм. По табл. П23 принимаем т = 2 мм.

Определяем число зубьев шестерни и колеса по (87), (86):

zj = 2a_w/[m (и+ 1)] =2 -150/[2 (3,5+ 1)] =33,4. Принимая Zx = 33, находим z₂ — иг_х — 3,5-33 = 119.

Вычисляем делительные диаметры, диаметры вершин зубьев и диаметры впадин шестерни и колеса по (83), (84), (85): для закрытой передачи

d_x = mz_x = 2-33 = 66 мм; с/₂ = /иг₂ = 2-119 = 238 мм;

d_ai = di+2m = 66+2-2 = 70 _мм; d_a2 = rf₂ + 2m = 238+2-2 = 242 мм;

d_/1 = d₁—2,5m = 66—2,5-2 = 61 мм; d_/2 = d₂—2,5m = 238—2,5-2 = 233 мм;

для открытой передачи

</₁₌=_тг₁₌₌з,5-20 = 70 мм; 4₂ = /яг₂ = 3,5-70 = 245 мм;

d_ai = di+2m = 80+ 2-3,5 = 87мм; d_a2 = d₂+2m = 245+2-3,5 = 238 мм;

d_/x=d_x—2,5m=80—2,5-3,5=71,25 мм; d_/2=d₂—2,5m=245—2,5-3,5=236,25 мм.

8. Уточняем передаточное число, межосевое расстояние и находим ширину зубчатых колес:

для закрытой передачи tt = z₂/Zi = 119/33 = 3,61; a_w = Q_y5(d_x + d₂) =0,5 (66+238) = 152 мм; b = ty_baa_w = 0,4-152 = 60,8 мм, принимаем 6₂ = 60 мм, Ь_х — Ь2 мм;

б) для открытой передачи (« = 3,5) a_w=0,5 (dt+d₂) = 0,5 (70+245) = 157,5 мм; 6 = i|Wl = 0,9.70 = 63 мм, принимаем Ь₂ = 63 мм, 6^ = 65 мм.

9, Определяем окружную скорость и назначаем степень точности передачи:

v_чак« = ndiHi/60 = п • 66 • 10 - ³.735/60 = 2,54 м/с; vогкр = ^ni/60 = я• 70.10-³• 735/60 = 2,7 м/с.

По табл. 2 при 2 м/с < с/ < 6 м/с принимаем 8-ю степень точности для открытой и закрытой передач.

10. Вычисляем силы, действующие в зацеплении, по формулам (88), (89): для закрытой передачи

F_t = 2Т j[dt = 2 • 240.10³/66 = 7,06.10³ Н, /⁷г=^^^а==/:,Иг20^о=-7,06.10³.0,364=2.57.10³ Н; для открытой передачи

F_t = ZT^di = 2.240.10³/70 = 6,86.10^е* Н, /> = F* tga = 6,86.10³.0,364 = 2,5-10³ Н. И. Проверка на прочность.

Для закрытой передачи рабочие контактные напряжения проверяем по фор­муле (90). Определяем коэффициенты, входящие в формулу (90): Z//=l,76 (см. занятие 8); 2^ = 274-10³ Па*/2 (_См, табл. П22); Z_e — по формулам (96а) и (97) при р=0°:

е_а « [1,88-3,2 (1/Zi+ 1/г₂)] cos р = [1,88—3,2 (1/33+1/119)] cos 0° = = [1,88—3,2 (0,0303+0,0084)]i =[1,88—0,124] = 1,756;

Z_e= /(4- e_a)/3= V(4-1,756)/3 = /"67748 = 0,865,

Коэффициенты нагрузки Кн ^и Кр— см. занятие 8.

По табл. П26 для 8-й степени точности, твердости ^HRC45, г/_закр = 2,54 м/с» интерполируя, получаем: /(/^=1,07; /Cf_v = 2/C//_v—1 = 2-1,07—1 = 1,14. Следо­вательно, АГ_я = /Сяэ/Сяг,=-Ь08.1,07 = 1,16; K_F=-KFfiK_Fv = 1,115.1,14 = 1,27.

Итак,

„ 7 7 7 1./*"^Ft ₇fi 974 103 л Qfi* "l/¹ »¹6' 7,06 ■ 10³ (3,61 + 1)

а_я=г_яад У _dihu -1,76-274-103.0,865 |/ _66<60.₁₀-₆,_3>6i = 417-10³ /2,65-10° = 680-10^б Па<о_я/>.

Выносливость зубьев по напряжениям изгиба проверим по уравнению (92) при наименьшем значении a_Fp/Yp для шестерни, так как Y'_E > Y"_F (см, табл, П27). По табл. П27, интерполируя, находим при Zi = 33

K_F = 3,85 при z = 30 1 ДУ>=0,10 при Дг=10\ __0,Ю-3__{А АО} К/?=3,75 при г = 40 / л: — 3 J *~"П(Г~~~Следовательно, У> _Ш) = Y_Pт)—х = 3,85 —0,03 = 3,82. Итак, по формуле (92) получаем

ар = YpK_FFtl(b₂m) =3,82-1,27-7,06/(60• 10-^0,03,

³.2) = 286• 10⁶ Па. Перенапряжение при о> = 286 МПа

[(Gp-v_Fp)/o_Fp] 100% = [(286—230J/230] 100% = 24,3% > 5%. Конечно, такая передача для эксплуатации непригодна. Получить необходимое соответствие между параметрами и прочностными ха­рактеристиками проектируемой передачи можно тремя способами: а) увеличить габариты передачи, т. е. увеличить a_w\ б) не изменяя межосевого расстояния, увеличить модуль при пропорциональном сокращении числа зубьев; в) улучшить качество материала зубчатых колес,

а) Принимая 0^ = 160 мм, из формулы (94) получаем

т = (0,01.. .0,02) = (0,01.. .0,02) 160= 1,6.. .3,2.

По табл. П23 принимаем т = 2,5 мм. Тогда

2! = 2a_w/[m (и+1)] = 2.160/[2,5 (3,5+1)] = 28,4.

Принимая zi = 28, получаем: z₂ = uz_Y = 3,5-28 = 98;

t/i = m2! = 2,5-28 = 70 мм; d₂ = mz₂ = 2,5-98 = 245 мм;

a_w = 0,5 (di + d₂) = 0,5 (70+ 245) = 157,5 мм.

Для получения a_wt выражающегося целым числом миллиметров, увеличим z₂ на два зуба, т. е. примем г₂ = Ю0. Это приведет к крайне незначительному изменению передаточного числа, что не имеет практического значения. Тогда

d₂ = //2z₂ = 2,5-100 = 250 мм, fl_tt,=¹/₂ (di + d₂) = V₂ (70+250) = 160 мм.

При этом Ь = ^ьа^ат^0.4-160=64 мм. Принимаем 6₂ = 64 мм, ^ = 66 мм. Окружная сила и окружная скорость:

F_t = 2T₁fd₁ = 2-240-10³/70 = 6,86 • 10³ Н;

v = лс/хЛх/60 = л - 70 -10 - ³.735/60 = 2,69 м/с,

т. е. можно оставить 8-ю степень точности: /С/? =1,27, У>(₂₈₎ « 3,88. Итак,

Y_FK_FF_t 3,88-1,27-6,87 _{olo 1Лв п} o_F= \ ^{г г}= _ал ' _ч ' =212-10⁶ Па < о>». ^Г Ь₂т 64-10~³-2,5 б) Примем т = 3 мм, определим число зубьев шестерни и колеса и проверим прочность зуба шестерни на изгиб при 0^=152 мм:

z₁ = 2a_w/[m (и +1)1 = 2-152/(3 (3,61 + 1)1=22; 2₂ = uz₁ — 3,61 -22 = 79,4, принимаем г₂ = 79. Y_F « 4,1 при Zx = 22 (см. табл. П27), следовательно,

о> = Y_FK_FF_tl(b₂m) = 4,1 -1,27 - 7,06/(60 -10 - ^ги

³ - 3) = 204 -10^е Па < c_FP.

в) Улучшаем качество материала. Принимая сталь 20Х, цементацию с закалкой до HRC52...62, по табл. П28 получаем o°_fp = o_FP = 280 МПа « 0/7=286 МПа.

Анализируя рассмотренные способы повышения соответствия между парамет­рами и прочностными характеристиками передачи, приходим к следующему выводу.

При увеличении габаритов передачи (а^ = 160мм, £₂ = 64 мм) масса и стои­мость передачи возрастут, что, конечно, следует считать недостатком варианта а). Достоинство этой передачи в ее повышенной плавности работы, так как число зубьев шестерни и колеса больше, чем при расчете по варианту б). Предпочти­тельными являются варианты б) и в), обеспечивающие меньшие габариты пере­дачи (a_w=152MM, 6₂ —60 мм), меньшую массу и стоимость. Эти варианты и использует практика расчета.

Заметим, что при низкой твердости рабочей поверхности зубьев, т. е. в слу­чае применения нормализованных или улучшенных сталей (<НВ350), для шес­терни следует выбирать возможно большее число зубьев (мелкомодульную пере­дачу), так как у передач с низкой твердостью рабочих поверхностей зубьев потери на трение в зацеплении примерно обратно пропорциональны числам зубьев шес­терни и колеса.

Итак, окончательные параметры закрытой передачи могут соответствовать расчетным: т — 2 мм, 0^=152 мм,... В случае повышения твердости зубьев принимают варианты в) или б): т = 3 мм, а^=152 мм, а^ = 66мм, d₂ = 238 мм, b_l = 62 мм, b₂ = 60 мм, zi = 22, z₂ = 79, и = z₂/z_x = 79/22 = 3,59;

^«1 = ^1 + 2/72 = 66 + 2-3 = 72 мм; d_e2 = tf₂ + 2m = 238 + 2-3 = 244 мм;

dj^di — 2,5w = 66—2,5 • 3 = 58,5 vm; d_f2 = tf₂—2,5m = 238—2,5 -3 = 230,5мм.

Прочность зубьев запроектированной открытой передачи проверим по урав­нениям (90) и (92) при Ztf=l,76, 2^ = 274.10^81/2:

Кн=КньК_Ну = 1,08» 1 = 1,08; K_p=Kf&Kfv = 1Л15* 1 = 1,115 (см. занятие 8); Z_e = У (4—б_а)/3= j/"(4—1,675)/3= |/0J74==0,88; е_а«[ 1,88—3,2 (1/Z-.+ 1/Z_a)] cos 0 = [ 1,88—3,2 (1/20+ 1/70)] cos 0^е = = [ 1,88—3,2 (0,05+0,0143)]1 = 1,675;

п -7 7 7 ^/ШШ+Е 1 7fi 974 103 _{fl яя 1}/Ш^б-10³ (3,5+1)_ ^=^ZmZ₈ J/ _rfiM =1,76-274. 103.0,88]/ 70-63-10-^3,5 ~

= 424 -10³ V^r2,16-10^e=625-10⁶ Па < а_НР\

YfK_fFj 4,12-1,115-6,86-10³ ,._{0 1Л6ГГ} . °г=-ь5г= 63-3,5-10-в "143-1»Па<а„.

Из рассмотренного примера проектирования нереверсивной открытой и за­крытой прямозубых цилиндрических передач с поверхностной твердостью зубьев > НВ350 можно сделать некоторые выводы:

61. Основным критерием прочности зуба закрытой передачи оказались не контактные напряжения, а напряжения изгиба. Следовательно, при высокой твер­дости зубьев параметры закрытой передачи определяют из условия выносливости зубьев на изгиб [см. формулу (93)], а проверку выполняют по формуле (90).

62. Габариты и масса открытой передачи (a_w = 157,5 мм, &₂ = 63 мм) больше, чем закрытой (0^=152 мм, 6₂ = 60 мм), а вращающий момент на выходном валу Т₂ меньше [так как меньше КПД, см. формулу (17)].

63. Так как основным критерием прочности зуба открытой передачи является напряжение изгиба, то проектирование передач из материалов с высокой поверх­ностной твердостью нерационально, так как выкрашивание наблюдается очень редко. Из-за плохой смазки и обилия абразива поверхностные слои зубьев исти­раются раньше, чем в них появляются усталостные трещины.

Задача 22. Вычислить допускаемую мощность закрытой нереверсивной пря­мозубой цилиндрической передачи, если: а) л₁=1500 мин*¹, Zi = 23, z₂ = 92, m = 4 мм, материал—сталь 45; термообработка—улучшение для шестерни и нор­мализация для колеса; б) /и = 980 мин~*, Zi = 25, z₂ = 125, m = 3 мм, материал шестерни и колеса—сталь 50Г.

Решение, а) 1. По формуле (86) определяем передаточное число:

и = z₂/z₁ = 92/23 = 4.

2. Вычисляем делительные диаметры [см. формулу (83)], межосевое расстоя- ние [см. формулу (87)], окружную скорость и назначаем степень точности пере- дачи:

d₁ = mz₁ = 4-23 = 92 мм; d₂ = mz₂ = 4-92 = 368 мм; д_и, = 0,5(с/₁ + с/₂) = (92+368)=230 мм; v = nd_xn j/60 = я - 92 -10 - ³ • 1500/60=7,23 м/с.

По табл. 2 принимаем 7-ю степень точности передачи.

3. Назначаем ресурс передачи и определяем допускаемые напряжения. Принимая длительный срок службы передачи (ресурс *₄^а10⁴), получаем

Khl^Kfi^I.

По табл. П28 для материала колеса (нормализация) 0^=430МПа, о$,_р=155 МПа для нереверсивной передачи; для шестерни (улучшение) а^_р = 600 МПа, о>р = 195 МПа для нереверсивной передачи. Итак, по формулам (98) и (101) на­ходим допускаемые напряжения:

для колеса

°нр = ^анрКн1. = 430-1 = 430 МПа; о}_р = o»_fPK_fl = 155-1 = 155 МПа, для шестерни

^анр ^(j0hp^khl = 600 -1 = 600 МПа; о^ = o*_fpKfl = 195 • 1 = 195 МПа.

б. По табл. П27, интерполируя, находим коэффициент формы зуба: У> = 4,12 при z = 20 \ Д}>=0,16—Az = 5 \ ^0,16-2^ _т У>=3,96 при z = 25 J х—2 / * 5

Следовательно, для шестерни (zi = 23)

Y'_F = Y_Fm) + д: = 3,96+0,064 = 4,024.

Для колеса (г₂ = 92) У>₍₈₀₎ = 3,74; У>(1₀о) = 3,75, принимаем Y"_F — 3,745₉

6. Сравниваем прочность зуба шестерни и колеса при изгибе:

&_FPlY'_F = 195/4,024 =48,5 МПа, o'>_FplY"_F = 155/3,745 = 44,5 МПа.

Так как прочность зуба колеса при изгибе оказалась ниже, чем шестерни, то дальнейший расчет выполняем по колесу.

7. Вычисляем окружную скорость и определяем значения коэффициентов, входящих в формулу (91) и (93):

v = nd 1Л1/6О = л; • 92 • 10 - ³ -1500/60 = 7,23 м/с.

При у = 7,23 м/с по табл. 2 принимаем 7-ю степень точности передачи.

8. По табл. П22 для прямозубых стальных колес /С_Л = 4950 Па^1/3.

9. Коэффициент ширины зубчатых колес г|?г,_д = 6/а^ = 0,315...0,5 при сим- метричном расположении зубчатых колес относительно опор; принимая г|)&_а = 0,41, получаем b₂ = tyba^aw — 0,41 -230 = 94,3 мм « 94 мм. По формуле на с. £6 полу- чаем г|)м = 0,5г|)_&Л(и+1) = 0,5-0,41 (4+1) = 1,025. По табл. П25 при ty_bd « 1 и твердости зубьев < НВ350 получаем /(яр = 1,04 и /Ор = 1,08.

0,08—2 \ 0,08-0,77 _{Л ЛОЛО}

Кх = =0,0308;

дг-0,77 Г 2

10. По табл. П26, интерполируя, определяем значения динамических коэф- фициентов при твердости <:НВ350:

/(//г, = 1,24 при у = 6 м/с

/С/л, = 1.32 при v = 8 м/с

/С/л>= 1.32 — 0,0308 « 1,29 при v = 7,23 м/с; /^ = 2/^—1=2-1,29—1 = 1,58 (см. примечание 2 к табл. П26).

Итак, коэффициенты нагрузки: K_h=KhrK_Hv = 1,04-1,29 = 1,34; Kf=Kf^Kfv = 1,08-1,58 = 1,71.

11. Из уравнений (91) и (92) находим значения крутящего момента и окруж- ную силу:

т -Г ^aw Уи^ьа (°нрУ_\ 230-Ю-³ у 4-0,41 -(430-10»)» ¹ Ue(«+l)J /Сяэ [4950(4 + 1)] 1,04

= 0,8-292 = 234 Н-м, принимаем [7\]=234 Н-м;

Y_FK_FF_t^ _г ^Ь₂торр 94-4-Ю-⁸-155- 10^е _01К1П,_и

^^=s-^£sf^J<aff; ^ "ТрТ*^ OTTTI =9.I5.I0»H_f

принимаем [i^] =9,1 -10³ Н.

12. Вычисляем допускаемую мощность:

из условия контактной выносливости зубьев

[Р] = [7\] л_х/9,55 = 234-1500/9,55 = 36,7-10³ Вт = 36,7 кВт;

из условия выносливости зубьев при изгибе

[Р] = [F,]y = 9,bl0³.7,23 =65,8-10³ Вт = 65,8 кВт.

Следовательно, для заданной закрытой передачи допускаемая мощность [Р] = 36,7 кВт из условия контактной выносливости зубьев.

Занятие 10. НЕПРЯМОЗУБЫЕ ЦИЛИНДРИЧЕСКИЕ ПЕРЕДАЧИ

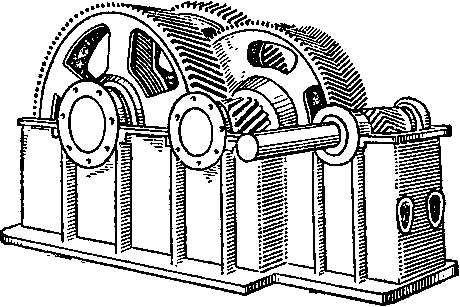
Косозубые и шевронные цилиндрические передачи

Передачи с косыми и шевронными зубьями (рис. 68) имеют на­клон контактной линии к основанию зуба, утолщение зуба в опас­ном сечении, большее значение коэффициента перекрытия и большую

J
1	у
t	i. i ?-
х—
б

суммарную длину контактных линии, поэтому такие передачи прочнее прямозубых, имеют плавный ход вследствие постепенного входа зубьев в зацепление (не сразу по всей длине, как у прямозубых) и работают относительно бесшумно даже при высоких скоростях.

Р

F_ag0scc_t

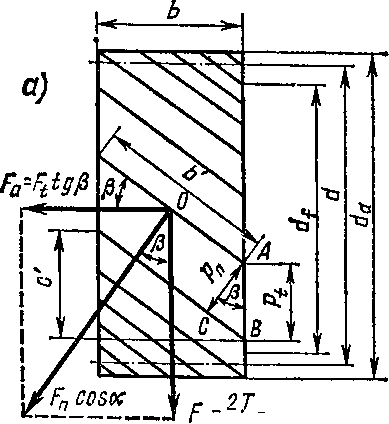
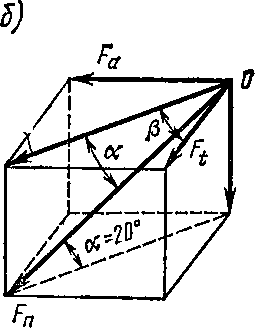
ис. 69

Недостатком косозубой передачи является наличие осевой силы F_a, стремящейся сдвинуть колесо вдоль оси вала (рис. 69, я).

Применение сдвоенных косозубых колес, зубья которых накло­нены в противоположные стороны, или шевронных колес (рис. 70), зуб которых выполнен в виде ^/ЛО£ (угол шеврона), устраняет осевую силу: F_a = \F'_a\ = F_ttg$> где (5 — угол наклона линии зуба (угол наклона боковой поверхности зуба к образующей поверхности делительного цилиндра зубчатого колеса).

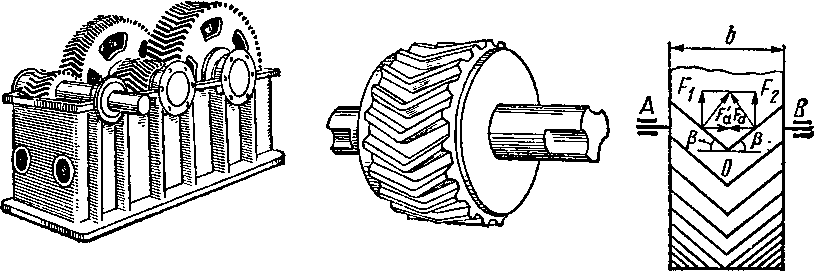
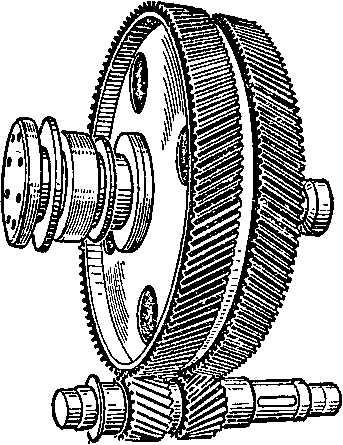
Ш евронные колеса работают плавно, их зубья обладают боль­шой прочностью. Эти колеса могут передавать большие мощности при высоких окружных скоростях (до 60...70 м/с), а шевронные колеса, имеющие проточку (рис. 71), передают еще большие мощности.

Зубья косозубых и шевронных ко­лес, как и прямозубых, могут быть нарезаны методами копирования (на фрезерных станках) или обкатки (на зубодолбежных или зубофрезерных станках). Быстроходные косозубые или шевронные зубчатые колеса типа тур­бинных нарезают почти исключительно на зубофрезерных станках.

Косозубые колеса обычно нарезают с р^8...20°, а шевронные — с р » 25...40°. *

Косозубые и шевронные колеса не рекомендуется применять в тихоход- ных передачах, так как более про- Рис. 71 стые и сравнительно дешевые прямо- зубые цилиндрические передачи достаточно хорошо работают при низких окружных скоростях.