2.3. Составление дифференциальных уравнений систем автоматического управления

Имея дифференциальные уравнения элементов си­стемы и уравнения связей, можно получить дифферен­циальное уравнение всей системы автоматического управления. При исследовании САУ обычно необхо­димо знать поведение выходной координаты систе­мы, а не всех ее элементов. Поэтому можно от систе­мы уравнений, описывающих поведение элементов, пу­тем исключения промежуточных переменных перейти к одному уравнению. Это уравнение будет содержать только выходную координату системы, а также внеш­ние воздействия. Зная внешние воздействия, прило­женные к системе, и решив дифференциальное урав­нение, можно найти реакцию системы управления на эти воздействия.

Для ознакомления с процессом составления диф­ференциального уравнения системы вначале рассмо­трим случай, когда объект управления и управляющее устройство описываются линейными дифференциаль­ными уравнениями 1-го порядка. Пусть имеем уравне­ние объекта

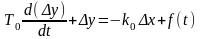(2.3.1)

и уравнение управляющего устройства

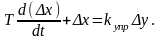(2.3.2)

Запишем уравнение всей системы управления относи­тельно Δу. Для этого найдем из уравнения (2.3.1) ве­личину Δх и ее производную:

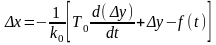, (2.3.3)

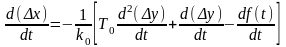. (2.3.4) Подставив выражения для Δх и d(Δx)/dt в уравне­ние (2.3.2), получим уравнение системы автоматиче­ского управления:

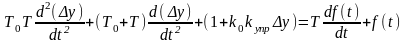. (2.3.5)

Таким образом, если объект управления и управляю­щее устройство описываются дифференциальными уравнениями 1-го порядка, то система управления в целом описывается дифференциальным уравнением 2-го порядка.

Пусть теперь объект по-прежнему описывается уравнением (2.3.1), а управляющее устройство описы­вается дифференциальным уравнением 2-го порядка

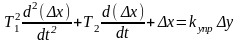. (2.3.6)

Для составления дифференциального уравнения си­стемы управления в этом случае найдем вторую про­изводную от Δх:

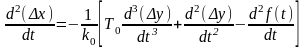. (2.3.7)

Подставив в уравнение (2.4.6) выражения для Δх, d(Δx)/dt и d²(Δx)/dt², получим искомое уравнение для системы управления:

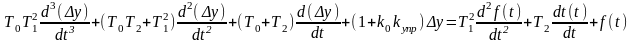(2.3.8)

Это дифференциальное уравнение 3-го порядка.

Аналогично получаются уравнения для системы управления в тех случаях, когда объект управления и управляющее устройство описываются дифференци­альными уравнениями более высоких порядков.

Таким образом, для получения дифференциаль­ного уравнения системы управления необходимо полу­чить вначале дифференциальные уравнения для объ­екта управления и управляющего устройства. В том случае, когда управляющее устройство состоит из не­скольких элементов, для составления дифференциаль­ного уравнения системы можно предварительно соста­вить дифференциальное уравнение управляющего устройства по дифференциальным уравнениям его эле­ментов. Исключая из полученных уравнений промежу­точные величины, можно получить дифференциальное уравнение относительно интересующих нас величин. Но, как правило, эти преобразования очень трудоемки и громоздки.

Для того чтобы упростить решения данной и дру­гих задач, в теории автоматического управления вме­сто рассмотрения величин, характеризующих состоя­ние системы во времени, - оригиналов рассматривают соответствующие им изображения, полученные при помощи преобразования Лапласа.

Рассмотрим в качестве примера звено, описывае­мое линейным дифференциальным уравнением 1-го порядка

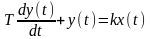. (2.3.9)

Используя преобразование Лапласа, получим:

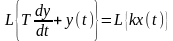. (2.3.10)

Отсюда в соответствии с правилами преобразования Лапласа

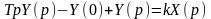. (2.3.11)

В этом уравнении x(t) и y(t) - оригиналы, а Х(р) и Y(p) - соответствующие им изображения. Решая ура­внение (2.3.11) относительно Y(p), получим

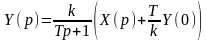. (2.3.12)

Обозначим W(p)=k/(Tp+1). В часто встречаю­щемся случае, когда начальное значение Y(0) = 0, уравнение (2.3.12) примет простой вид

Y(p) = W(p)X(p). (2.3.13)

Функция W(p), зависящая от параметров звена, оп­ределяющая связь между изображениями выходной и входной величин, называется передаточной функцией звена. Таким образом, в нашем примере передаточная функция звена имеет вид

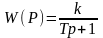. (2.3.14)