7.2. Основные характеристики случайной функции

Основными характеристиками случайной функции являются математическое ожидание, дисперсия и кор­реляционный момент (корреляционная функция). Рас­смотрим эти характеристики.

Математическим ожиданием случайной функции X(t) называют неслучайную функцию m_x(t), значение, которой при каждом фиксированном значении аргу­мента t равно математическому ожиданию сечения,, соответствующего этому фиксированному значению аргумента: m_x(t)=М[X(t)], то есть математическое ожидание случайной функции можно рассматривать как «среднюю кривую» (среднюю - по множеству реализаций), около которой расположены отдельные реализации случайной функции рис. 7.1). Зная одно­мерную плотность распределения вероятностей f₁(x; t}, можно найти m_x(t):

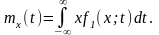(7.2.1)

Дисперсией случайной функции X(t) называют не­случайную неотрицательную функцию D_x(t), значение которой при каждом фиксированном значении аргу­мента t равно дисперсии сечения, соответствующего этому фиксированному значению аргумента: D_x(t)=D[X(t)]. Дисперсия характеризует степень рассеяния возможных реализаций вокруг математического ожи­дания случайной функции. В соответствии с опреде­лением дисперсия

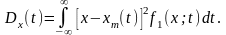(7.2.2)

Часто в качестве рассеяния рассматривается сред­нее квадратичное отклонение случайной функции σ_х(t)

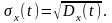(7.2.3)

Корреляционной функцией случайной функции X(t) называют неслучайную функцию K_x(t₁,t₂) двух независимых аргументов t₁ и t₂, значение которой при каждой паре фиксированных значений аргументов равно корреляционному моменту сечений, соответст­вующих этим значениям аргументов:

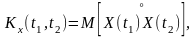(7.2.4)

где

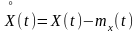(7.2.5)

- центрированная случайная величина. Из определе­ния корреляционной функции следует, что

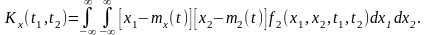(7.2.6)

Корреляционная функция характеризует зависи­мость между случайными величинами X(t₁) и X(t₂) - сечениями случайной функции при t₁=t и t=t₂. Чем меньше связь между сечениями, тем меньше значение корреляционной функции. Это означает, что значения, принимаемые случайной функцией, быстро изменяют­ся. На рис. 7.2 показаны реализации двух случайных функций X(t) и Y(t) с одинаковыми математическими ожиданиями и дисперсиями. Случайная функция X(t) изменяется быстрее, и связь между сечениями мень­ше, чем для функции Y(t), то есть корреляционная функ­ция для X(t) меньше, чем для Y(t).

Нетрудно заметить, что при равных значениях аргумента (t=t₁=t₂) корреляционная функция случайной функции равна дисперсии этой функции: K_x(t, t)=D_x(t). Действительно, учитывая, что

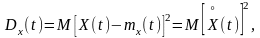
имеем

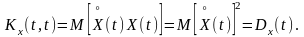
Из свойств корреляционной функции отметим сле­дующие:

1. При перестановке аргументов корреляционная функция не изменяется:

К_х(t₁,t₂)=К_x(t₂,t₁). (7.2.7)

2. Прибавление к случайной функции X(t) неслу­чайного слагаемого φ(t) не изменяет ее корреляцион­ной функции:

Y(t)=X(t) + φ(t), К_у(t₁, t_z)=К_х(t₁, t₂). (7.2.8)

3. При умножении случайной функции X(t) на не­случайный множитель φ(t) ее корреляционная функ­ция умножается на произведение φ(t₁)φ(t₂). Пусть Y(t)=X(t)φ(t). Тогда, по определению корреляцион­ной функции имеем

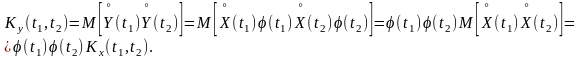(7.2.9) 4. Для всякой корреляционной функции справедливо неравенство

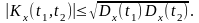(7.2.10)

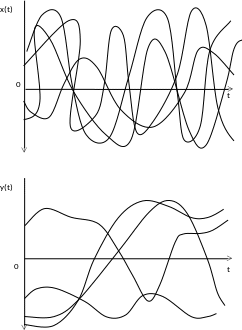
Рисунок 7.2

Для того чтобы оценить степень зависимости сече­ний двух случайных функций, вводят характеристи­ку - взаимную корреляционную функцию. Взаимной корреляционной функцией двух случайных функ­ций X(t) и Y(t) называют неслучайную функцию K_xy(t₁, t₂) двух независимых аргументов t₁ и t₂, значе­ние которой при каждой паре фиксированных значе­ний аргументов равно корреляционному моменту се­чений обеих функций, соответствующих фиксирован­ным значениям аргументов:

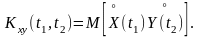
Для того чтобы отличить взаимную корреляционную функцию от корреляционной функции, последнюю на­зывают автокорреляционной функцией. Две случай­ные функции X(t) и Y(t) называют некоррелирован­ными, если их взаимная корреляционная функция то­ждественно равна нулю, то есть K_хy(t₁,t₂)≡0.

Рассмотрим, как преобразуются основные характе­ристики случайных функций - математическое ожидание и корреляционная функция при проведении над ними линейных операций. Математическое ожидание суммы двух случайных функций равно сумме матема­тических ожиданий слагаемых: если Z(t)=X(t)+Y(t), то m_z(t)=m_x(t)+m_y(t). Найдем корреля­ционную функцию суммы двух корреляционных слу­чайных функций Z(t):

(7.2.11)

Учитывая, что 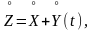имеем

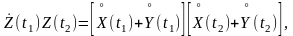
откуда

(7.2.12)

Из выражения (7.2.12) следует, что корреляционная функция двух некоррелированных случайных функций равна сумме корреляционных функций слагаемых, то есть

К_z(t₁,t₂)=К_х(t₁,t₂)+К_у(t₁,t₂). (7.2.13)