Вопрос 42 Параллелепи́пед — призма, основанием которой служит параллелограмм, или (равносильно) многогранник, у которого шесть граней и каждая из них параллелограмм

Типы параллелепипеда

Различается несколько типов параллелепипеда:

• Прямоугольный параллелепипед — это параллелепипед, у которого все грани прямоугольники;

• Прямой параллелепипед — это параллелепипед, у которого 4 боковые грани прямоугольники;

• Наклонный параллелепипед — это параллелепипед, боковые грани которого не перпендикулярны основаниям.

• Куб — это прямоугольный параллелепипед с равными измерениями. Все шесть граней куба — равные квадраты.

Свойства

• Параллелепипед симметричен относительно середины его диагонали.

• Любой отрезок с концами, принадлежащими поверхности параллелепипеда и проходящий через середину его диагонали, делится ею пополам; в частности, все диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам.

• Противолежащие грани параллелепипеда параллельны и равны.

• Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.

Вопрос 43 Пирами́да (др.-греч. πυραμίς, род. п. πυραμίδος) — многогранник, основание которого — многоугольник, а остальные грани — треугольники, имеющие общую вершину^[1]. По числу углов основания различают пирамиды треугольные, четырёхугольные и т. д. Пирамида является частным случаем конуса Усечё́нная пирами́да — многогранник, образованный пирамидой и её сечением, параллельным основанию. Правильная пирамидаПирамида называется правильной, если основанием её является правильный многоугольник, а вершина проецируется в центр основания. Тогда она обладает такими свойствами:

• боковые рёбра правильной пирамиды равны;

• в правильной пирамиде все боковые грани — конгруэнтные равнобедренные треугольники;

• в любую правильную пирамиду можно как вписать, так и описать вокруг неё сферу;

• если центры вписанной и описанной сферы совпадают, то сумма плоских углов при вершине пирамиды равна 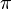, а каждый из них соответственно 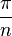, где n — количество сторон многоугольника основания^[8];

• площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.

Вопрос 44 Свойства параллельных сечений в пирамиде

74. Теорема. Если пирамида (черт. 83) пересечена плоскостью, параллельной основанию, то:

1) боковые рёбра и высота делятся этой плоскостью на пропорциональные части;

2) в сечении получается многоугольник (abcde), подобный основанию;

3) площади сечения и основания относятся, как квадраты их расстояний от вершины.

Вопрос 45  Призмой называется многогранник, в основаниях которого лежат многоугольники, а боковые грани являются параллелограммами. Основания призмы представляют собой равные многоугольники, лежащие в параллельных плоскостях.

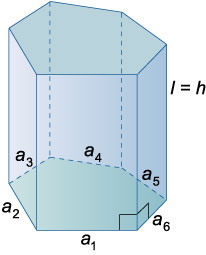
 Призма называется прямой, если ее боковые ребра перпендикулярны основаниям. В противном случае призма является наклонной.

 Если основаниями призмы являются параллелограммы, то такая призма называется параллелепипедом. В частном случае, когда в основаниях находятся прямоугольники, и призма является прямой, она называется прямоугольным параллелепипедом.

 Прямая призма называется правильной, если в ее основаниях лежат правильные многоугольники. В частности, если основания и боковые грани призмы являются квадратами, то такая призма называется кубом.

 Площадь боковой поверхности правильной призмы S_бок = P_осн l = (a₁ + a₂ + ... + a_n)l, где P_осн − периметр основания призмы, a₁, a₂, ..., a_n − стороны основания, l − длина бокового ребра (в прямой призме боковое ребро совпадает с высотой h).

 Площадь боковой поверхности наклонной призмы S_бок = pl, где p − полупериметр перпендикулярного сечения призмы, l − боковое ребро.

Вопрос 46 Боковая поверхность правильной усеченной пирамиды равна произведению полусуммы периметров оснований на апофему:

1.	Sбок= 1 2 (p1+ p2) a

Вопрос 47 Тела вращения — объёмные тела, возникающие при вращении плоской геометрической фигуры, ограниченной кривой, вокруг оси, лежащей в той же плоскости. Вращение вокруг оси x Объём тела, образуемого вращением вокруг оси фигуры, ограниченной функцией на интервале , осью и прямыми и равен: Вращение вокруг оси y Объём тела, образуемого вращением вокруг оси фигуры, ограниченной функцией на интервале , осью и прямыми и равен:

Вопрос 48 Поверхность вращения — поверхность, образуемая при вращении вокруг прямой (оси поверхности) произвольной линии (прямой, плоской или пространственной кривой). Например, если прямая пересекает ось вращения, то при её вращении получится коническая поверхность, если параллельна оси — цилиндрическая, если скрещивается с осью — однополостный гиперболоид вращения. Одна и та же поверхность может быть получена вращением самых разнообразных кривых.

Вопрос 49 Шар — геометрическое тело; совокупность всех точек пространства, находящихся от центра на расстоянии, не больше заданного. Это расстояние называется радиусом шара. Шар образуется вращением полукруга около его неподвижного диаметра. Этот диаметр называется осью шара, а оба конца указанного диаметра — полюсами шара. Поверхность шара называется сферой: замкнутый шар включает эту сферу, открытый шар — исключает.

Вопрос 50 Объем параллелепипедаО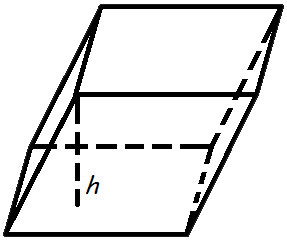 бъем параллелепипеда равен произведению площади основания на высоту.Формула объема параллелепипеда V = S_o · h

где V- объем параллелепипеда, S_o- площадь основания, h- длина высоты.

Вопрос 51 Объем усеченной пирамиды равен одной трети произведения высоты h (OS) на сумму площадей верхнего основания S1 (abcde), нижнего основания усеченной пирамиды S2 (ABCDE) и средней пропорциональной между ними.

1.	V= 1 3 h(S1+ S1 S2 + S2)

Вопрос 52 сеченный конус получится, если в конусе провести сечение, параллельное основанию. Тело ограниченное этим сечением, основанием и боковой поверхностью конуса называется усеченным конусом. См. также Площадь поверхности усеченного конуса

Объем усеченного конуса вычисляется по формуле:

1.	V= 1 3  π h(r12+r1·r2+r22)

Вопрос 53 Ко́мпле́ксные^[1] чи́сла (устар. мнимые числа^[2]) — числа вида , где и  — вещественные числа,  — мнимая единица; то есть . Множество всех комплексных чисел обычно обозначается от лат. complex — тесно связанный.