
- •Область применения мк. Достоинства и недостатки.
- •2. Состав и структура стали
- •7. Основы расчета мк
- •8. Соединения мк.
- •9.Расчет изгибаемых элементов
- •10.Расчет центрально и внецентренно растянутых элементов металлических конструкций
- •11.Расчет центрально-сжатых элементов мк
- •12.Расчет внецентренно сжатых элементов мк
- •Преимущество металлических колонн
- •Элементы стальных колонн
- •Виды колонн
- •Монтаж колонн
7. Основы расчета мк
Метод расчета строительных конструкций по предельным состояниям. Предельное состояние-такое состояние конструкции, при котором она перестает удовлетворять заданным эксплуатационным требованиям. При этом нормальная эксплуатация здания или сооружения становится невозможной. Нормальная эксплуатация-которая осуществляется без ограничений в соответствии с нормами и обеспечивается безопасное пребывание людей, штатная работа оборудования и сохранность ограждающих конструкций.
Предельные состояния: первая группа: все виды разрушений (вязкое(пластическое), хрупкое, усталостное), потеря устойчивости сжатых конструкций, чрезмерные пластические деформации, приводящие к качественному изменению конфигурации конструкций, неупругие сдвиги в соединениях. Расчет выполняется на расчетные значения нагрузок.
Вторая группа: сверхнормативные прогибы, амплитуды колебаний и отклонения от вертикали колонн. Расчет выполняется на нормативные значения нагрузок.
Цель расчета по предельным состояниям –не допустить ни одного из возможных предельных состояний при минимальном расходе материалов.
8. Соединения мк.
По принципу образования соединения делятся на три группы:
Механические: кованые, болтовые, заклепочные, самосверлящий самонарезающий винт(саморез), пороховые дюбели, вытяжные заклепки
Сварные: электродуговая сварка, полуавтоматическая сварка
Клеевые или клееболтовые
9.Расчет изгибаемых элементов
Проверяется прочность, устойчивость общая и местная, деформации. Изгиб может быть в одной и двух плоскостях (плоский и косой). Проверки могут делаться по упругой иупруго-пластической стадии работы материала. Поскольку сталь на начальной стадии работы наиболее близко подходит к идеально упругому телу, рассматриваемому в сопротивлении материалов, расчет часто ведется по формулам этой дисциплины или приведенным к ним.
При расчете на прочность в упругой стадии нормальные напряжения проверяются по 2-й стадии работы сечений (см. рис. 4.1).
Нормальные напряжения при плоском и косом изгибе проверяются по формулам:
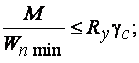
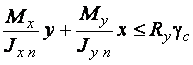 .
.
Касательные напряжения проверяются по формуле Журавского
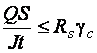 .
.
При
наличии отверстий вводится коэффициент 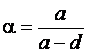 ,
где а –
шаг отверстий; d –
диаметр отверстий.
,
где а –
шаг отверстий; d –
диаметр отверстий.
При
наличии местных напряжений ![]() (см.
рис. 3.3) стенка балки проверяется по
условию
(см.
рис. 3.3) стенка балки проверяется по
условию
![]()
где 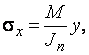
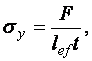
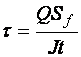 ,
, ![]() ; t –
толщина стенки балки;
; t –
толщина стенки балки; ![]() –
статический момент сечения пояса балки
относительно ее центра тяжести;
–
статический момент сечения пояса балки
относительно ее центра тяжести; ![]() толщина
пояса проверяемой балки; b –
ширина полки
вышележащей балки; J –
учитывается с коэффициентом а (см.
выше).
толщина
пояса проверяемой балки; b –
ширина полки
вышележащей балки; J –
учитывается с коэффициентом а (см.
выше).
Проверка общей устойчивости балки производится по формуле
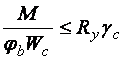 ,
,
где ![]() принимается
по [1, прил. 7], при этом последовательно
определяются
принимается
по [1, прил. 7], при этом последовательно
определяются ![]()
![]()
![]()
![]()
![]() для
сжатого пояса.
для
сжатого пояса.
При
достаточной ширине сжатого пояса
балки ![]() меньше
или равной предельных значений [1, табл.
8], либо при передаче нагрузки через
сплошной жесткий настил, непрерывно
опирающийся на сжатый пояс, – проверки
общей устойчивости можно не делать
(
меньше
или равной предельных значений [1, табл.
8], либо при передаче нагрузки через
сплошной жесткий настил, непрерывно
опирающийся на сжатый пояс, – проверки
общей устойчивости можно не делать
(![]() пояс
балки).
пояс
балки).
Проверка деформаций при плоском и косом изгибах выполняется по формулам:
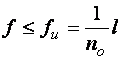 ,
, 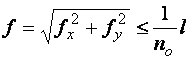 .
.
Деформации
определяются от воздействия моментов
по нагрузкам с коэффициентом ![]() .
.
Расчет на прочность при пластической работе материала может выполняться для разрезных балок сплошного постоянного сечения из сталей с пределом текучести до 530 МПа, несущих статическую нагрузку. Он ведется по 3-й стадии, когда в сечении имеется упругое ядро. В балках переменного сечения расчет с развитием пластических деформаций допускается только для одного, наиболее загруженного сечения.
Положение
нейтральной оси в этом случае определяется
из условия ![]() :
:
![]()
нейтральная ось делит площадь сечения пополам. Воспринимаемый сечением момент найдем из условия
![]() ,
, ![]() ,
, ![]()
Обозначим ![]() ,
тогда
,
тогда ![]() и
и ![]()
где ![]() пластический
момент сопротивления.
пластический
момент сопротивления.
Вычислим его для прямоугольного сечения:
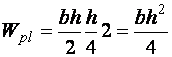 .
.
Найдем соотношение между пластическим и упругим моментами сопротивления:
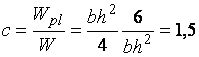 ,
,
отсюда ![]() .
Но сечение по 4-й стадии работать не
может, пластические деформации стали
ограничены. Для ограничения больших
деформаций необходимо упругое ядро.
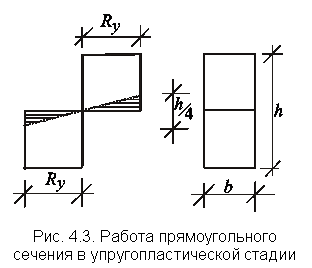
Допустим полные деформации в 4 раза
больше упругих, т. е. упругое ядро
сечения имеет высоту, равную 1/4 h (рис.
4.3). Потеря в моменте сопротивления
.
Но сечение по 4-й стадии работать не
может, пластические деформации стали
ограничены. Для ограничения больших
деформаций необходимо упругое ядро.
Допустим полные деформации в 4 раза
больше упругих, т. е. упругое ядро
сечения имеет высоту, равную 1/4 h (рис.
4.3). Потеря в моменте сопротивления
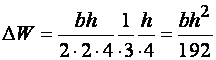 ,
,
что в относительных единицах составляет
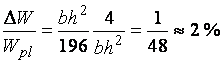 .
.
|
С
учетом наличия упругого ядра Расчет на прочность разрезных балок сплошного сечения по упруго-пластическому моменту сопротивления, на нагрузку, действующую в одной из главных плоскостей, следует выполнять по формулам:
На косой изгиб расчет по пластическим моментам сопротивления следует выполнять по формуле
|
При
тех же условиях и 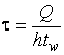 ≤
0,5
≤
0,5![]() .
Здесь
.
Здесь ![]() –
толщина стенки, h –
высота.
–
толщина стенки, h –
высота.
Расчет
опорных сечений балок в этих случаях
(при ![]()
![]() и
и ![]() )
следует выполнять по формуле
)
следует выполнять по формуле 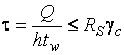 .
.
При
наличии зоны чистого изгиба (![]() на
значительной длине)
на
значительной длине) ![]() ,
, ![]()
![]() заменяются
на
заменяются
на ![]() ,
, ![]() и
и ![]() (
(![]() среднее
значение).
среднее
значение).
При одновременном действии в сечении момента M и поперечной силы Q коэффициент с1 следует определять по формулам:
при ![]()
![]() при
при ![]()
![]() ,
где
,
где
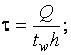
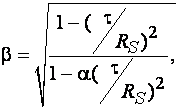
здесь а – коэффициент, равный 0,7 для двутаврового сечения, изгибаемого в плоскости стенки, и 0 – для других типов сечений; с – коэффициент, принимаемый по [1, табл. 66];с1 – коэффициент, принимаемый не менее 1 и не более коэффициента с.

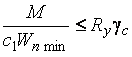 ,
, 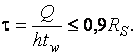
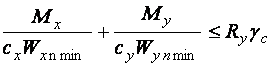 .
.