15. Определение математической модели экономической задачи.

Основой для решения экономических задач являются математические модели.

Линейное программирование — наука о ме­тодах исследования и отыскания экстремальных (наибольших и наименьших) значений линейной функции, на неизвестные которой наложены линейные ограничения.

Эта линейная функция называется целевой, а ограничения, которые математически записываются в виде уравнений или неравенств, называются системой ограничений.

Математическое выражение целевой функ­ции и ее ограничений называется математической моделью экономической задачи.

В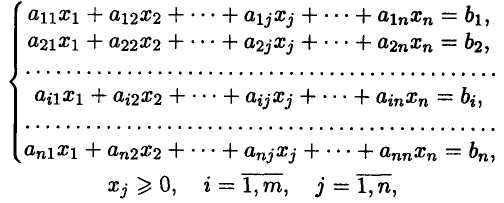 общем виде математическая модель задачи линейного программирования (ЛП) записывается как: Z(x)=C₁X₁+C₂X₂ + ^... +С_JX_J +^…+С_nX_n max(min)

при ограничениях: (*), где X_i — неизвестные; a _ij , b_j , C_i — заданные постоянные вели­чины.

Математическая модель в более краткой записи имеет вид: Z(x) = ∑C_i X_i max(min)

Допустимым решением (планом) зада­чи линейного программирования называется вектор X = (х₁, х₂, ,...х_n ) , удовлетворяющий системе ограничений.

Множество допустимых решений образует область допус­тимых решений (ОДР).

Д опустимое решение, при котором целевая функция достигает своего экстремального значения, называ­ется оптимальным решением задачи линейного программиро­вания и обозначается Х_опт.

Базисное допустимое решение:

Является опорным решением, где r— ранг системы ограничений.

16. Виды математических моделей линейного программирования.

Математическое выражение целевой функ­ции и ее ограничений называется математической моделью экономической задачи.

Математическая модель задачи ЛП может быть каноничес­кой и неканонической.

Если все ограничения системы заданы урав­нениями и переменные Xj неотрицательные, то такая модель задачи называется канонической.

Если хотя бы одно ограничение является неравенством, то модель задачи ЛП является неканонической. Чтобы перейти от неканонической модели к канонической, необходимо в каждое

неравенство ввести балансовую переменную х_n+i .

Если знак неравенства <, то балансовая переменная вводится со знаком плюс, если знак неравенства >, то — минус. В целевую функ­цию балансовые переменные не вводятся.

Чтобы составить математическую модель задачи ЛП, не­обходимо:

— ввести обозначения переменных;

— исходя из цели экономических исследований, составить целевую функцию;

— учитывая ограничения в использовании экономических показателей задачи и их количественные закономернос­ти, записать систему ограничений.

17. Составление математической модели.

Основой для решения экономических задач являются математические модели.

Линейное программирование — наука о ме­тодах исследования и отыскания экстремальных (наибольших и наименьших) значений линейной функции, на неизвестные которой наложены линейные ограничения.

Эта линейная функция называется целевой, а ограничения, которые математически записываются в виде уравнений или неравенств, называются системой ограничений.

Математическое выражение целевой функ­ции и ее ограничений называется математической моделью экономической задачи.

В общем виде математическая модель задачи линейного программирования (ЛП) записывается как: Z(x)=C₁X₁+C₂X₂ + ^... +С_JX_J +^…+С_nX_n max(min)

при ограничениях: (*), где X_i — неизвестные; a _ij , b_j , C_i — заданные постоянные вели­чины.

Математическая модель в более краткой записи имеет вид: Z(x) = ∑C_i X_i max(min)

Допустимым решением (планом) зада­чи линейного программирования называется вектор X = (х₁, х₂, ,...х_n ) , удовлетворяющий системе ограничений.

Множество допустимых решений образует область допус­тимых решений (ОДР).

Допустимое решение, при котором целевая функция достигает своего экстремального значения, называ­ется оптимальным решением задачи линейного программиро­вания и обозначается Х_опт.

Составление математической модели включает:

• выбор переменных задачи

• составление системы ограничений

• выбор целевой функции

Переменными задачи называются величины Х1, Х2, Хn, которые полностью характеризуют экономический процесс. Обычно их записывают в виде вектора: X=(X₁, X₂,...,X_n).