34. Графы. Основные понятия.

Граф - это математическое понятие, которое служит для моделирования связей между объектами. Различают ориентированные и неориентированные графы.

Неориентированным графом G называется пара конечных множеств (V,E), где V - произвольное множество объектов, называемых вершинами и Е{{i,j}|i,j  V} множество неупорядоченных пар вершин, где {i,j}  Е называется ребром.

Ориентированным графам (орграфам) называется пара конечных множеств G’=(V, A), где V - множество вершин, и A {(i,j)|i,j  V} множество упорядоченных пар вершин, где А(i,j) – называется дугой. Если i, j – это дуга, то i наз. Непосредственным предшественником j, а j непосредственным последователем i-го.

Количество дуг, входящих в вершину i наз. Степенью захода этой вершины, а кол-во дуг, выходящих из вершины i наз. Степенью исхода из этой вершины. В неориентированном графе вершины i, j наз. Концами ребра. Матрицы смежности графа G(V,E) наз. Матрица А=||а i,j ||n*n c элементами а i,j =1, если {i,j}  Е и а i,j =0 если {i,j} не принадлежат Е.

Маршрутом в неориентированном графе G наз. Последовательность вершин W=(  ,…  ), n>=0. Граф наз. Связным, если существует маршрут, связывающие любые 2 вершины и маршрут наз. Замкнутым если n>0 и .

35. Построение эйлерова цикла.

Замкнутый маршрут, кот. включает каждое ребро графа ровно 1 раз наз. Эйлеровым маршрутом, а граф, кот. содержит такой маршрут наз. Эйлеровым графом. Задачу, является ли граф эйлеровым впервые поставил и решил Эйлер в 1736 г Он писал: «В городе Кенигсберг есть 2 острова, кот. соединяются семью мостами » 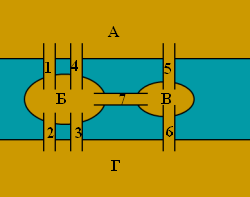Вопрос: можно ли спланировать прогулку так, чтобы ииз четырех участков суши А, Б, В, Г пройти по каждому мосту 1 раз и вернуться в начальный пункт.

Критерий эйлеровости

Теорема:

Для того, чтобы граф   был эйлеровым необходимо чтобы: 1. Все вершины имели четную степень. 2. Все компоненты связности кроме, может быть одной, не содержали ребер.

36. Алгоритм построения эйлерова цикла

Предполагается, что неориентированный граф G=(V_,E) связен и степени его вершин четны.

Шаг 0. Если граф несвязен, либо существует вершина нечетной степени, то конец эйлерова цикла не существует.

Шаг 1. Выбираем произвольную вершину v1 и полагаем частичный эйлеров цикл С^* ={v1}. В графе G будем двигаться от некоторой вершины частичного цикла и помечать пройденные ребра. Помеченное ребро будем включать в эйлеров цикл. Полагаем i=1.

Шаг 2. Двигаемся от вершины Vi по непомеченным ребрам и помечаем их до тех пор, пока не вернемся в vi. Пусть при этом построен цикл С.

Цикл С включаем в С* так, что вначале идут ребра С* до вершины vi, затем ребра цикла С и затем оставшиеся ребра С*.

Если все ребра исходного графа помечены, то эйлеров цикл построен. Если есть непомеченные ребра, то в силу связности графа должна существовать вершина Vj  С*_, которая является концом непомеченного ребра. Пусть Vj - последняя из таких вершин, входящая в С*.

Шаг 3. Удаляем из графа ребра цикла С. В оставшемся графе вершины будут по-прежнему иметь четную степень. Полагаем i=j и переходим к Шагу 2, т.е. строим новый цикл на непомеченных ребрах, начиная с вершины Vj.

Я