Общая постановка и задачи линейного программирования (злп)

Общая форма ЗЛП

Найти величины (x1, xn) доставляющие min (max) линейной целевой функции Z = c1x1+c2x2+…+cnxnmin(max) и удовлетворяющие ограничениям, которыми могут быть равенствами и неравенствами вида: a(1,1)x1+…+a(1,n)xn<=bi, i=1,k. a(I,1)x1+…+a(I,n)xn>=bi, i=k+1,l. A(k,1)x1+…+a(k,n)xn=bi, i=l+1,m. Xj>=0, j=1,5.

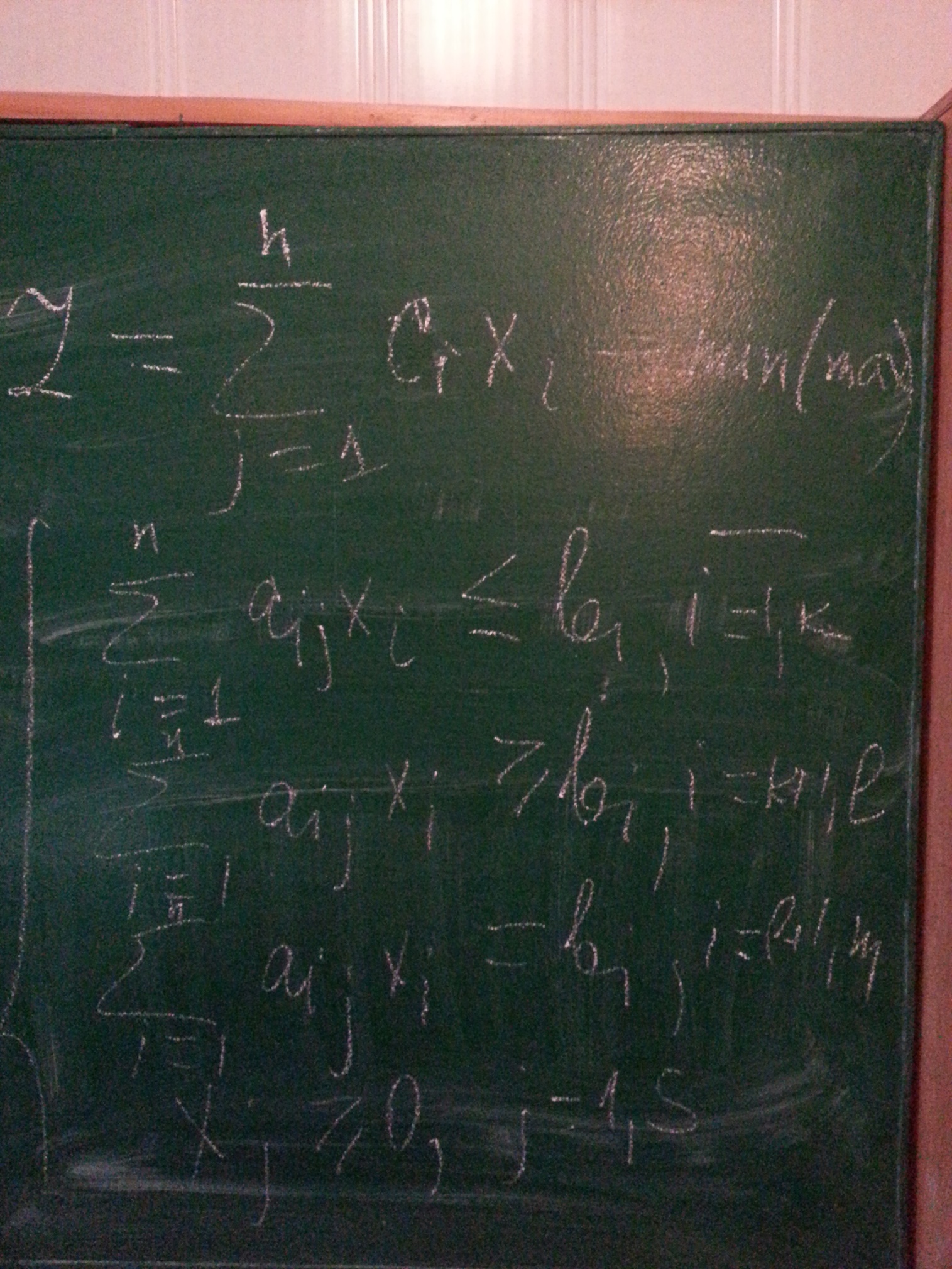
Стандартная и экономическая форма ЗЛП.

Различают 2 основные формы ЗЛП в зависимости от ограничений разного типа.

1. Стандартная форма

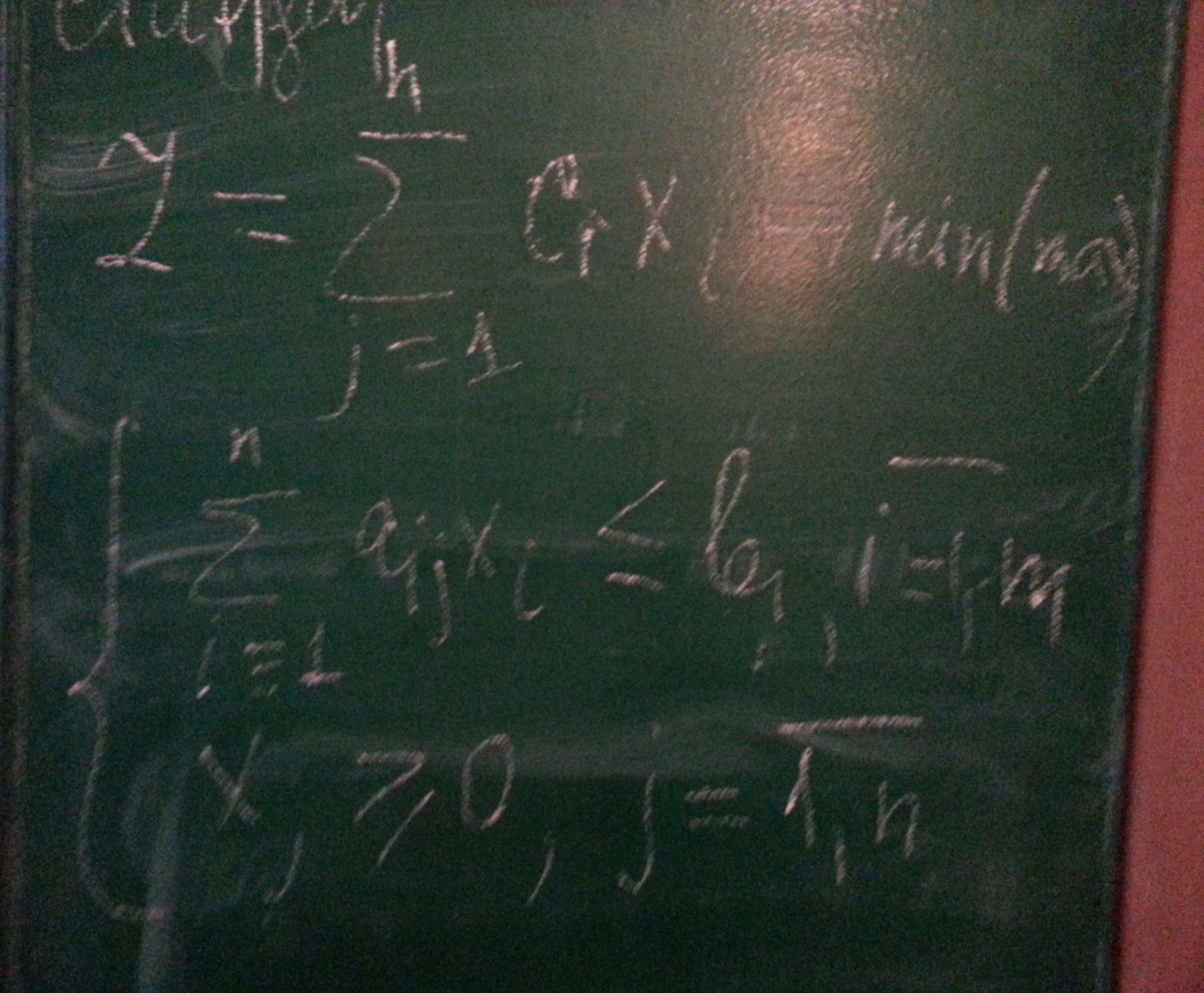
2. Каноническая форма ЗЛП

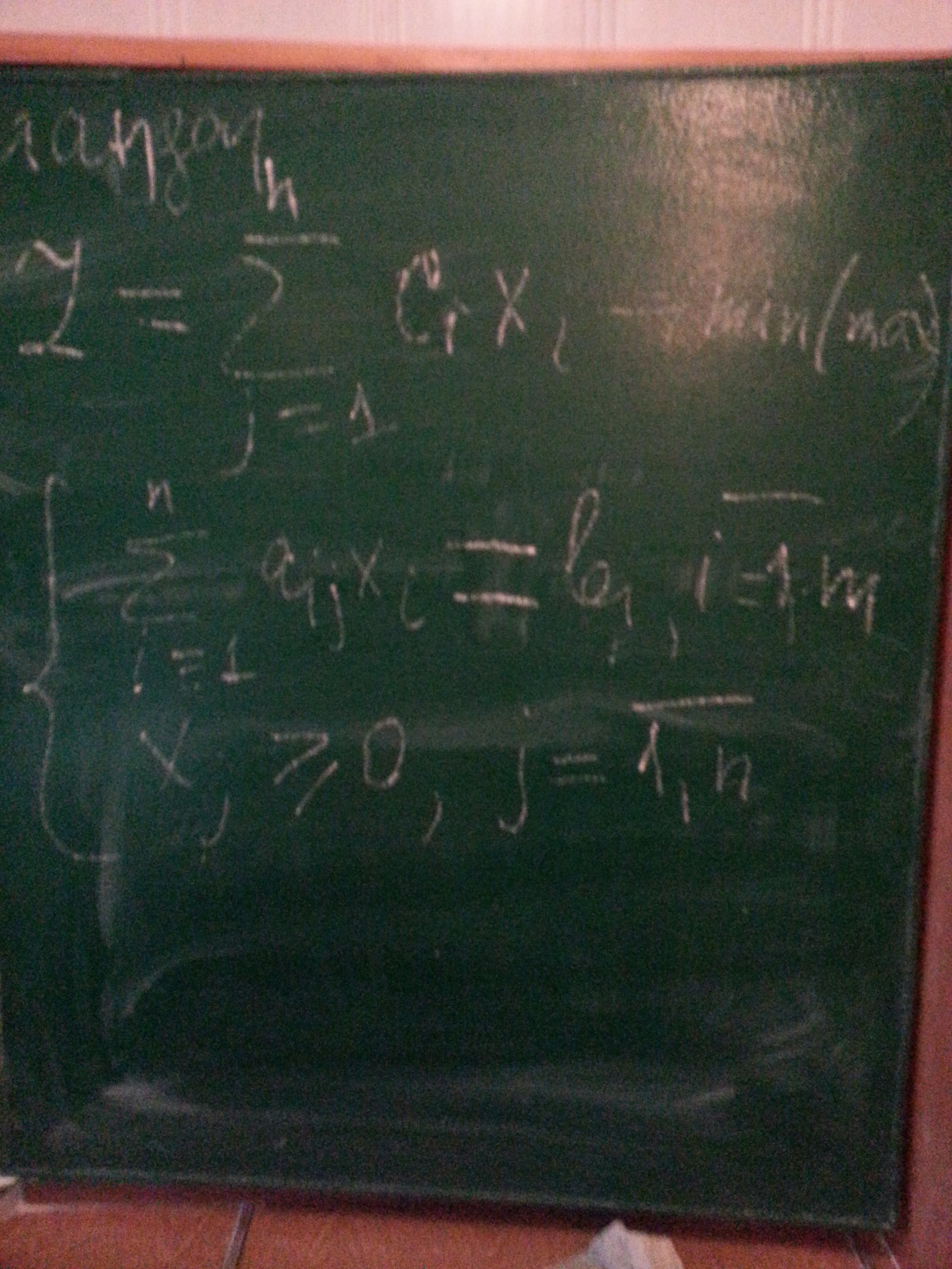
Стандартная форма ЗЛП интересная тем, что большинство прикладных задач естественным образом сводятся к этому виду модели. Каноническая форма ЗЛП важна потому, что основные вычислительные методы решения ЗЛП разработаны именно для этой формы.

3. Эквивалентность ЗЛП – представленные формы ЗЛП эквивалентны в том смысле, что каждая из них с помощью не сложных преобразований может быть приведена к любой из 2-х остальных. Следовательно, любую ЗЛП можно привести к каноническому виду.

   1. Переход от задачи минимизация к максимизации. Для этого нужно изменить знак целевой функции.

   2. Переход от ограничений неравенств к равенствам. Любое ограничение в форме неравенства вводом дополнительной неотрицательной переменной может превратиться в ограничение равенства.

   3. 

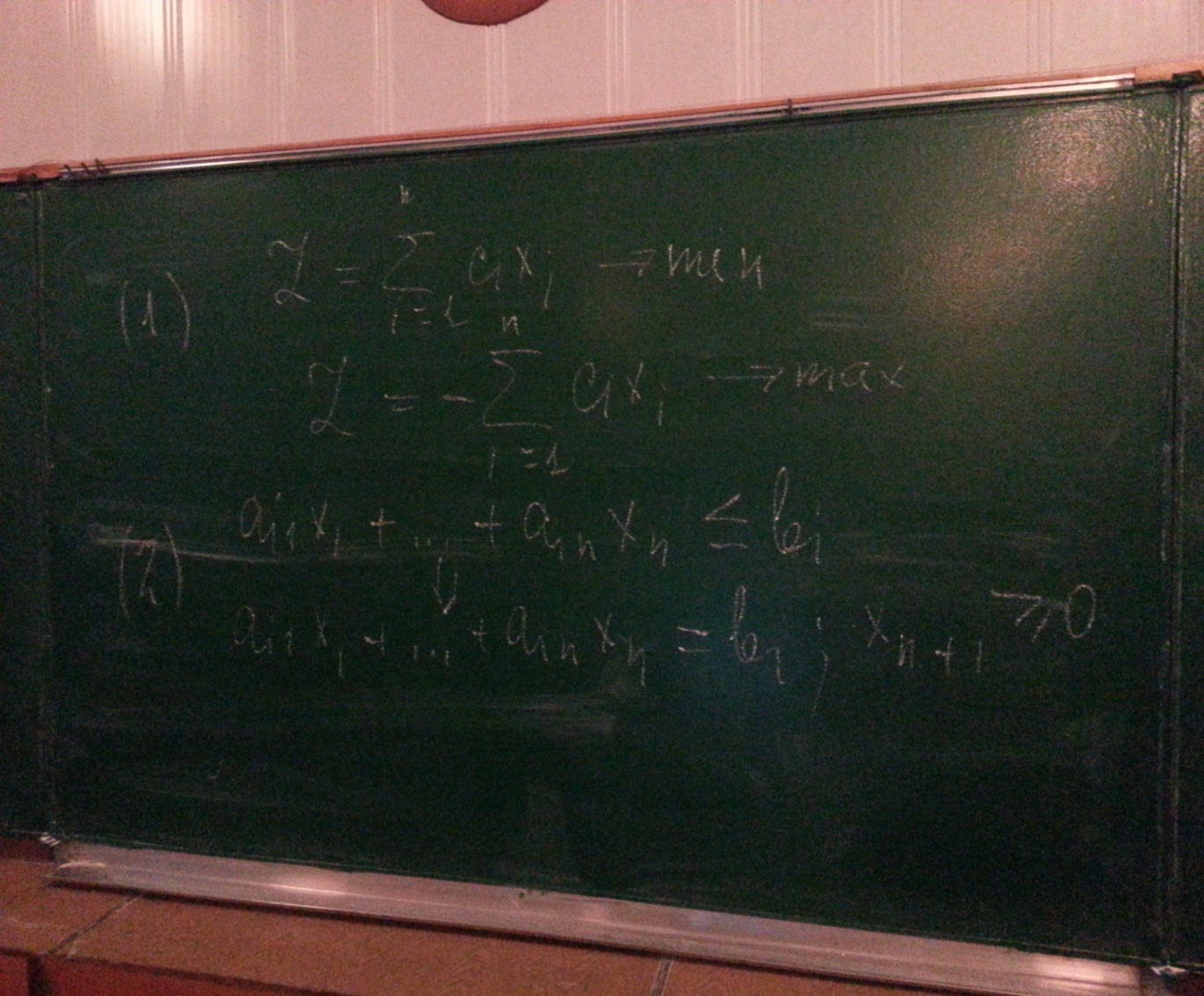
4. Геометрическая интерпретация ЗЛП в стандартной форме – область допустимых решений ЗЛП в стандартной форме образуется пересечением m-множеств, каждая из которых определяется соответствующим неравенством. И представляет собой полупространство, лежащее по одну сторону от гиперплоскости. Пересечение указанных полупространств является многогранником, которые и является областью допустимых решений задач и обозначается «Х». Линии уровня оптимизируемой функцией Z=с1x1+…+cnxn=const, образует семейство параллельных плоскостей. Вектор нормали к этим плоскостям c=(c1,…,cn). Он определяет направление возрастания целевой функции, а противоположный вектор «-С» направление убывания функции.

Множества точек удовлетворяющих ограничениям (Х) может быть пустым (*), ограниченным (**) и не ограниченным (***).

* - задача не имеет решений.

** - задача разрешима и имеет либо единственное решение совпадающие с одной из вершин многогранника «Х». Либо, бесконечное множество решений – ребро или грань многогранника, параллельные плоскостям семейству целевой функции.

*** - вопрос о разрешимости зависит от того ограниченна область сверху на множестве «Х» или нет. Если ограничена, то возвращаемся к «**». Если нет, решение отсутствует. Для максимизации определяется ограничение сверху, а для минимизации снизу.

Пример 1.

Решить геометрическим способом ЗЛП. Z=6x1+2x2max.

Ограничения:

1. 4x1+5x2<=61

2. -3x1+4x2<=24

3. 5x1-3x2<=30

4. –x1,x2>=0.

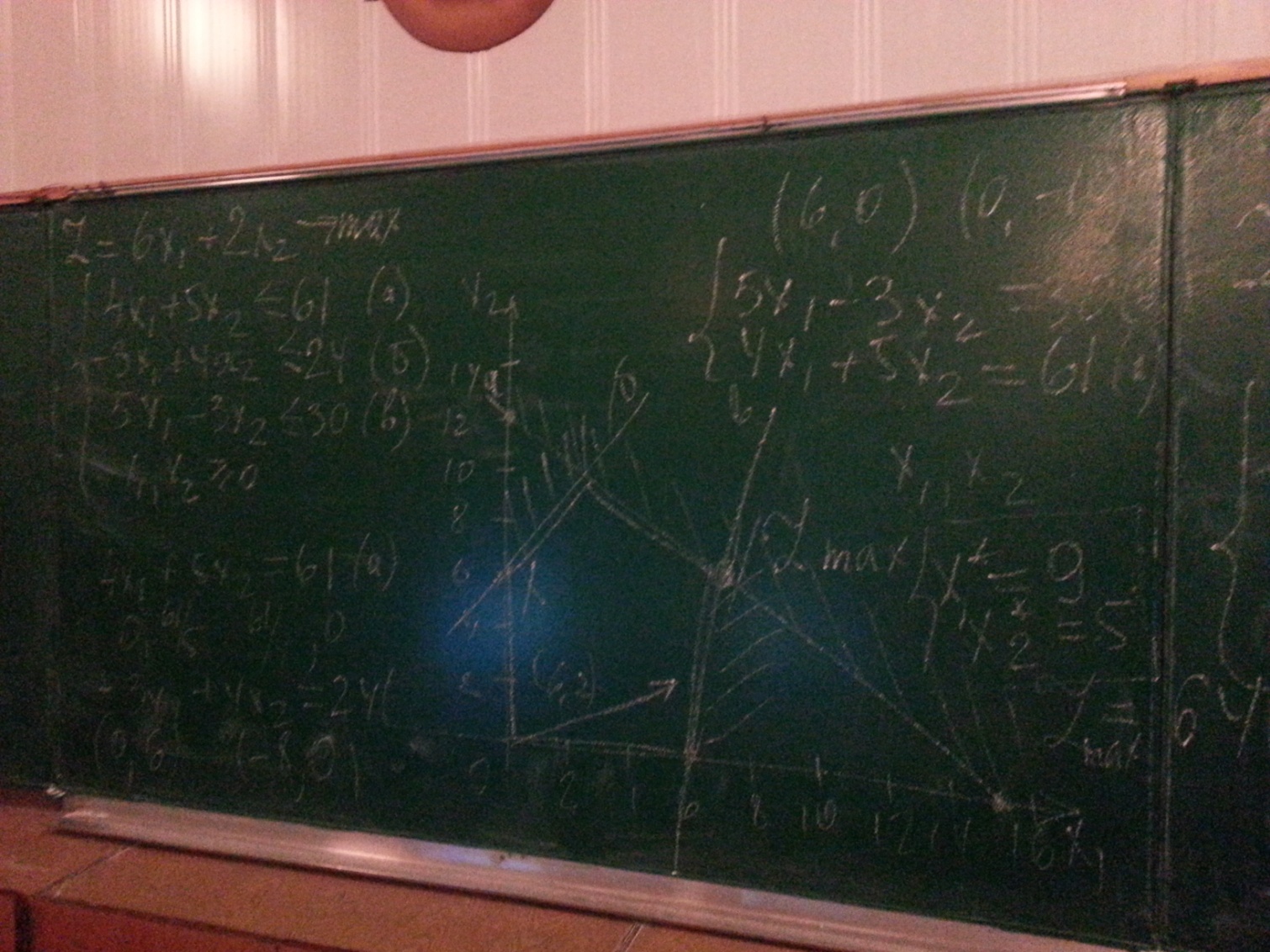
Пример 2.

Z=8x1+10x2max.

Ограничения:

1. X1+2x2<=220

2. 2x1+x2<=260

3. 4x1+5x2<=640

4. X1,x2>=0.

Z=8x1+10x2=const=1280 содержит вершины m1 и m2. Следовательно решений бесконечно много. Все точки ребра m2 – m3. Максимальное значение функции = 1280.