Нейтрон.

Аналогичные эксперименты были проведены также по рассеянию электронов на нейтронах. Оказалось, что внутри нейтрона также имеется электромагнитная структура. Распределение заряда приведено на рисунке 2а.

Очевидно, вблизи центра нейтрона располагается положительный заряд, а дальше от центра – отрицательный. Площади, ограниченные кривыми и осью абсцисс, равны, следовательно, положительный заряд равен отрицательному, и в целом нейтрон электрически нейтрален. Отметим, что размеры областей, в которых сосредоточены электрические заряды у протона и нейтрона примерно одинаковы.

Ч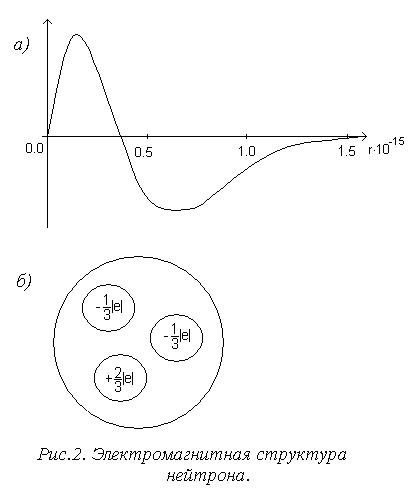 то означает непрерывное распределение электрического элементарного заряда? Ведь до настоящего времени не удалось обнаружить физических объектов с дробным зарядом. Каков же смысл утверждения, что в объеме находится небольшая часть элементарного заряда?

В настоящее время считается, что протон состоит из двух квазичастиц – кварков с зарядами +2 /3 и одного с зарядом- /3 (см. рис. 1б). Нейтрон наоборот состоит из двух кварков с зарядом - /3 и одного с зарядом +2 /3 (см. рис. 2б). Кварки непрерывно движутся. Их относительное время пребывания на различных расстояниях от центра может быть эффективно представлено в виде размазанности заряда по объему. В свободном состоянии кварки не обнаружены. В настоящее время считается, что их в принципе нельзя обнаружить в свободном состоянии, поскольку для этого надо затратить бесконечную энергию, а внутри протона и нейтрона они все же существуют. Такое допущение позволяет объяснить многие явления и поэтому принимается в качестве весьма вероятной гипотезы.

Спин и магнитный момент.

Кроме заряда частицы могут обладать моментом импульса, который называют спином. Спин не обусловлен вращением частицы вокруг оси, ибо для такого объяснения пришлось бы допустить наличие линейной скорости вращения, большей скорости света, что невозможно. Поэтому спин рассматривается как внутреннее свойство частицы и с ним связано наличие у частицы магнитных свойств, а именно наличие магнитного момента, который также не может быть объяснен движением заряда и рассматривается как первоначальное свойство частицы. Отметим, что в классической электродинамике магнитный момент может быть лишь результатом движения зарядов по замкнутым траекториям.

Поэтому спиновый магнитный момент частиц не может быть описан в классической теории электричества и магнетизма. Однако магнитное поле, обусловленное спиновыми магнитными моментами, может быть при необходимости описано феноменологически. Как правило, напряженность этого поля очень мала. Лишь в случае постоянных магнитов оно достигает больших значений. Классическая теория не в состоянии описать механизм возникновения этого поля, но само поле вне постоянных магнитов полностью описывается классической теорией.

Элементарный заряд и его инвариантность.

Мысль о дискретности электрических зарядов была впервые высказана Франклином в 1752 г., однако, как экспериментальный результат - дискретность электрических зарядов в принципе следует из открытых в 1834 г. М. Фарадеем (1791-1867) законов электролиза. Но этот вывод из законов электролиза был сделан лишь в 1881 г. Г.Л. Гельмгольцем (1821-1894) и Д. Стонеем (1826-1911). В 1895 г. Г. Лоренц (1853-1928) разработал теорию электромагнетизма, основывающуюся на представлении о реально существующих элементарных зарядах (электронах). Числовое значение элементарного заряда было теоретически вычислено на основании законов электролиза. А прямое экспериментальное измерение элементарного заряда было впервые выполнено Милликеном (1868-1953) в 1909 г.