23.Вывод уравнения непрерывности для электрического тока. Интегральная формулировка закона сохранения электрического заряда.

Если через некоторую поверхность переносится суммарный заряд, отличный от нуля, то говорят, что через эту поверхность течет электрический ток. Ток может протекать в твердых телах, в жидкостях и в газах. Для протекания тока необходимо наличие в данном теле (или в данной среде) заряженных частиц, которые могут перемещаться в пределах всего тела. Такие частицы называются носителями тока. Ими могут быть электроны, ионы либо макроскопические частицы (например, заряженные пылинки, капельки), несущие избыточный заряд. Направлением тока условились считать направление движения положительно заряженных частиц. Линии, вдоль которых движутся заряженные частицы, названылиниями тока. Для количественной характеристики электрического тока служат две основные величины: плотность тока и сила тока. Плотность тока равна заряду, проходящему в единицу времени через единицу поверхности, которая перпендикулярна к линиям тока. Пусть в единице объема содержится   положительных носителей тока и   отрицательных.  Алгебраическая величина зарядов носителей тока равна, соответственно,   и  . Если под действием поля носители тока приобретают средние скорости движения  и  , то за единицу времени через единичную площадку пройдет   положительных носителей тока, которые перенесут заряд  . Аналогично отрицательные носители перенесут в противоположную сторону заряд  . Таким образом, для плотности тока получается следующее выражение:

 .

Или в векторном виде вектор плотности тока j определяется следующим образом

 .

Если в поперечном сечении проводника выделить бесконечно малую площадку dS, перпендикулярную вектору плотности тока j, то заряд dq, проходящий через нее за время dt, равен

.

Сила тока в проводнике равна заряду, проходящему в единицу времени через полное сечение проводника. Если заряд dq, проходящий через сечение проводника за время dt, то

.

Сила тока скалярная величина. Зная вектор плотности тока в каждой точке проводника, можно выразить через него и силу тока 

.

Размерность силы тока - ампер (А), единица измерения плотности тока - ампер на метр квадратный ( ). Если сила тока не меняется во времени, то ток, протекающий в проводнике, называют постоянным. Силу постоянного тока будем обозначать буквой I. Рассмотрим среду, в которой течет ток, и выделим в ней замкнутую поверхность S(рис. 4.1). Для тока, выходящего в единицу времени из объема V, ограниченного поверхностью S, имеем

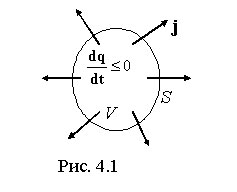
В силу закона сохранения заряда эта величина должна быть равна скорости убывания заряда, содержащегося в данном объеме

. Это соотношение называют уравнением непрерывности. Учитывая, что заряд 

 ,

получим  . Преобразовав левую часть равенства по теореме о дивергенции (теореме Гаусса - Остроградского), находим

 .

Таким образом в каждой точке пространства выполняется условие

,

которое является дифференциальной формой уравнения непрерывности.  Если токи постоянны, то все электрические величины не зависят от времени и в уравнении непрерывности нужно положить   равным нулю. Тогда  , следовательно, в случае постоянного тока вектор j не имеет источников. Это означает, что линии тока нигде не начинаются и нигде не заканчиваются, т. е. они замкнуты.

(7.2)