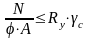42.Проверка общей устойчивости изгибаемых элементов.

(первое пре­дельное состояние). Изгибаемые элементы могут выйти из работы вслед­ствие потери ими общей устойчивости. При потере устойчивости изги­баемый элемент (например, балка) при расположении нагрузки в плос­кости главной оси инерции сначала изгибается в своей плоскости, затем при достижении нагрузкой критического значения начинает закручи­ваться и выходить из плоскости изгиба (рис. 3.15).

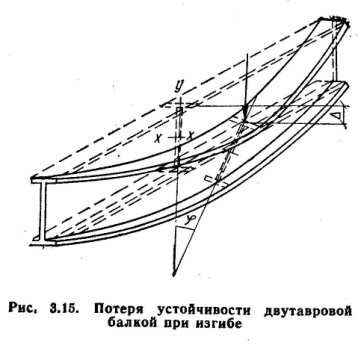
Проверка общей устойчивости балок сводится к сравнению возникающих напряжений с критическими. Расчетная формула этой проверки представима в виде:

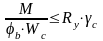
где W_c – момент сопротивления для сжатого пояса;

_b = _кр_у – коэффициент перехода от нормативных сопротивлений к критическим напряжениям потери общей устойчивости изгибаемыми элементами (обычно коэффициент _b называют балочным коэффициентом).

При определении значения _b за расчетную длину балки l _еf следует принимать расстояние между точ­ками закреплений сжатого пояса от поперечных сме­щений (узлами продольных или поперечных связей, точками крепления жесткого настила); при отсут­ствии связей l _еf = l (где l — пролет балки); за рас­четную длину консоли следует принимать l _еf = l при отсутствии закрепления сжатого пояса на конце консоли в горизонтальной плоскости (здесь l — дли­на консоли); расстояние между точками закреп­лений сжатого пояса в горизонтальной плоскости при закреплении пояса на конце и по длине консоли.

Устойчивость балок не требуется прове­рять:

а)при передаче нагрузки через сплошной жест­кий настил, непрерывно опирающийся на сжатый пояс балки и надежно с ним связанный (плиты железобетонные из тяжелого, легкого и ячеистого бетона, плоский и профилированный металличес­кий настил, волнистую сталь и т. п.);

б)при отношении расчетной длины балки l_еf к ширине сжатого пояса b, не превышающем значений, определяемых по формулам табл. 8* для балок симметричного двутаврового сечения и с более развитым сжатым поясом, для которых шири­на растянутого пояса составляет не менее 0,75 ширины сжатого пояса.

Проверка упругих деформаций, нарушающих нормальные условия эксплуатации (второе предельное состояние). В условиях нормального режима работы сооружения в балках могут появиться деформации, затрудняющие эксплуатацию конструкций. Эти деформации (прогибы) проверяют по упругой стадии работы конструкции от воздействия нормативных нагрузок. При этом возникающие максимальные прогибы не должны превышать предельных, приведенных в разделе 10 СНиП2.01.07-85*

f  f

43.Расчет элементов стальных конструкций на центральное сжатие

Предельные состояния сжатых жестких стержней определяются раз­витием пластических деформаций при достижении напряжениями пре­дела текучести, а гибких стержней — потерей устойчивости.

Расчет на прочность. Расчет на прочность центрально сжатых эле­ментов выполняется так же, как и центрально растянутых, по форму­лам (Р.1) и (Р.3). Вместе с тем в этом случае могут быть учтены не­которые отличительные особенности работы материала на сжатие. На­пример, проверка прочности элементов с соединениями на болтах повышенной прочности может быть выполнена по сечению «брутто», т. е. без учета ослабления сечения отверстиями.

При малой длине выступающей части сжатого элемента (например, опорное ребро балки) его сечение определяется расчетом на местное смятие торцевой поверхности (при наличии пригонки

Требования по проверке устойчивости цент­рально-сжатых стержней установлены в действующем СНиП П-23-81* на основе расчета внецентренно-сжатых стержней с учетом влияния формы сечения, на­чального искривления оси, случайного эксцентриси­тета сжимающей силы, а также соединительных эле­ментов (для сквозных стержней).

Начальные искривления или случайные эксцент­риситеты приняты в соответствии с допускаемыми отклонениями, установленными в нормах на изго­товление стальных конструкций.

При решении поставленной задачи был рассмот­рен внецентренно-сжатый стержень, схема которого приведена на рис.3, а.

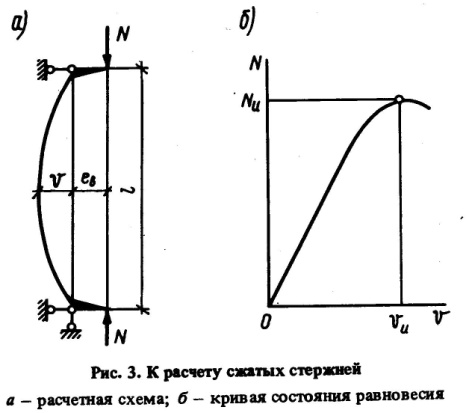
При этом решение выполня­лось в предположении малости перемещений по де­формированной схеме с учетом пластических де­формаций, а значение расчетной несущей способнос­ти принято равным предельному значению сжимаю­щей силы N_u, которая может быть воспринята эле­ментом (рис. 3, б). Форма изогнутой оси принима­лась по полуволне синусоиды.

В СНиП П-23-81* методика практичес­ких расчетов центрально-сжатых элементов приве­дена с использованием коэффициентов устойчивос­ти при центральном сжатии  (коэффициентов про­дольного изгиба), которые вычислены в зависи­мости от условной гибкости 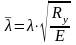и приня­ты равными  = N_u/ (А R_у).

При вычислении значений коэффициентов  типы поперечных сечений сжатых элементов принимались в соответствии со значениями коэффициентами влияния формы сечения (табл.73 СНиП П-23-81*), а началь­ные несовершенства е_b — по формуле

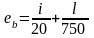
где i – радиус инерции сечения;

l – расчетная длина элемента.

При нормировании коэффициентов  определя­лась также критическая сила упругих идеальных стержней по методу Эйлера. Окончательные значе­ния коэффициентов  принимались наименьшими из двух: вычисленных с учетом начальных несовер­шенств или по методу Эйлера с введением коэффициента надежности _е = 1.3 (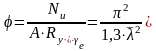 ). Это было сделано для ограничения прогибов сжатых стержней при относительно больших гибкостях, когда влияние начальных несовер­шенств станови­лось несущественным.

Полученные таким образом значения коэффици­ентов  для различных форм поперечных сечений были осреднены и аппроксимированы с помощью формул (8)-(10) СНиП П-23-81*, на основании ко­торых для различных значений расчетных сопротив­лений R_у, выраженных через приведенные гибкости была составлена табл. 72 СНиП П-23-81* коэффициентов продольного изгиба  для центрально-сжатых элементов.

Более точно эти величины можно определить по эмпирическим формулам.

В этом случае расчет на устойчивость сплошностенчатых элементов, подверженных центральному сжатию силой N следует выполнять по формуле