Концептуальная постановка задачи моделирования
это:
сформулированный в терминах конкретных дисциплин (физики, химии, биологии и т.д.) перечень основных вопросов, интересующих заказчика
совокупность гипотез относительно свойств и поведения объекта моделирования
В выборе и обосновании принимаемых гипотез в значительной степени проявляется искусство, опыт и знания, накопленные членами рабочей группы.
Согласно принятым гипотезам определяется множество параметров, описывающих состояние объекта, а также перечень законов, управляющих изменением и взаимосвязью этих параметров между собой
Отличие концептуальной постановки задачи
Концептуальная постановка задачи моделирования в отличие от содержательной постановки использует терминологию конкретной дисциплины (в рассматриваемом случае — механики).
При этом моделируемый реальный объект (мяч) заменяется его механической моделью (материальной точкой).
Фактически в приведенном примере концептуальная постановка свелась к постановке классической задачи механики о движении материальной точки в поле сил тяжести.
Концептуальная постановка более абстрактна по отношению к содержательной, так как материальной точке можно сопоставить произвольный материальный объект, брошенный под углом к горизонту: футбольный мяч, ядро, камень или артиллерийский снаряд
Дискретно-детерминированные модели. Конечный автомат Мили, конечный автомат Мура. Автоматы с памятью, без памяти, синхронные и асинхронные.Основные способы описания конечного автомата. Примеры
Если внешние воздействия, приложенные к системе (управляющие и возмущающие) являются определенными известными функциями времени u=f(t). В этом случае состоянии системы описываемой обыкновенными дифференциальными уравнениями, в любой момент времени t может быть однозначно описано по состоянию системы в предшествующий момент времени. Системы для которых состояние системы однозначно определяется начальными значениями и может быть предсказано для любого момента времени называются детерминированными.
Дискретные математические модели - это модели, в которых все переменные и параметры - дискретные величины.
Основным видом дискретно- детерминированных моделей является конечный автомат.
Конечным автоматом называют дискретный преобразователь информации, способный под воздействием входных сигналов переходить из одного состояния в другое и формировать сигналы на выходе. Это автомат с памятью. Для организации памяти в описание автомата вводят автоматное время и понятие состояние автомата.
Понятие «состояние» автомата означает, что выходной сигнал автомата зависит не только от входных сигналов в данный момент времени, но и учитывает входные сигналы, поступающие ранее. Это позволяет устранить время как явную переменную и выразить выходные сигналы как функцию состояний и входных сигналов.
Всякий переход автомата из одного состояния в другое возможен не ранее, чем через дискретный интервал времени. Причем сам переход считается, происходит мгновенно, то есть не учитывают переходные процессы в реальных схемах.
Пример:
Конечный автомат Мили.
Автомат Мили (англ. Mealy machine) — конечный автомат, выходная последовательность которого (в отличие от автомата Мура) зависит от состояния автомата и входных сигналов. Это означает, что в графе состояний каждому ребру соответствует некоторое значение (выходной символ). В вершины графа автомата Мили записываются выходящие сигналы, а дугам графа приписывают условие перехода из одного состояния в другое, а также входящие сигналы.
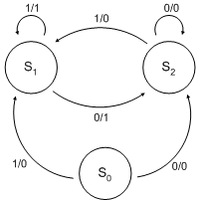
Пример: RS-триггер.
конечный автомат Мура
Зависимость выходного сигнала только от состояния представлена в автоматах типа Мура (англ. Moore machine). В автомате Мура функция выходов определяет значение выходного символа только по одному аргументу — состоянию автомата. Эту функцию называют также функцией меток, так как она каждому состоянию автомата ставит метку на выходе.
Примером простейшего автомата Мура является рассмотренный нами в примере №1 счетчик по модулю 2
