4.4. Операції з масивами

В Mathcad поряд з арифметичними операціями з масивами (рис.4.7.) можна виконувати такі операції, як транспонування, обертання, визначення матриці тощо.

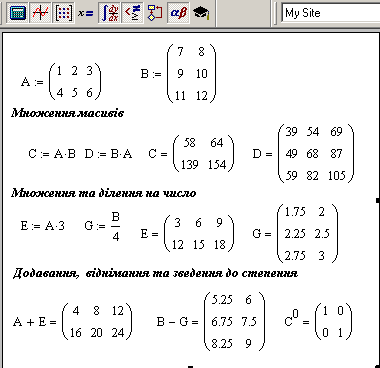
Рис.4.7. Арифметичні операції з масивами

Операція транспонування матриць полягає в тому, що рядки та стовпці міняються місцями. Транспонування матриці всікується встановленням праворуч вверху біля імені матриці літери Т. Це виконується спеціальною піктограмою (М) палітри Matrix або комбінацією клавіш <Ctrl> + <1>.

Знаходження оберненої матриці полягає в тому, що обернена матриця, будучи помножена на вихідну, в результаті дає одиничну матрицю. Це справедливо для не виродженої квадратної матриці. Ця процедура еквівалентна зведеню вихідної матриці до мінус першого степеня. На палітрі Matrix є піктограма (Х^-1), що дозволяє знайти обернену матрицю, рис.4.8.

Рис.4.8. Транспонування матриці, обчислення оберненої матриці

Для визначення детермінанта матриці необхідно ім’я матриці охопити прямими дужками, що виконується комбінацією клавіш <Shift> + <\> , або скористатися піктограмою |Х| на палітрі Matrix.

Обчислення векторного добутку матриць можна виконати з допомогою спеціального оператора, який вводиться натисненням клавіш <Ctrl> + <8> або скористатися піктограмою ( ) палітри Matrix. Для обчислення суми елементів вектора слід скористатися акордом клавіш <Ctrl> + <4>.

Певний інтерес представляє собою процедура векторизації. Хай масив є аргументом деякої функції, яка визначена для скалярних аргументів. Застосовуючи функцію векторизації, можна обчислити значення функції для кожного елемента заданого масиву. У результаті отримати масив тих же розмірів, що і заданий, а його елементи є результатом обчислення функції для аргумента, який знаходиться в вихідному масиві на відповідному місці. Для виконання векторизації на палітрі є спеціальна піктограма ( ), також можна скористатися комбінацією клавіш <Ctrl> + < – >. Перед застосуванням векторизації до певного виразу цей вираз має бути виокремлений, рис.4.9.

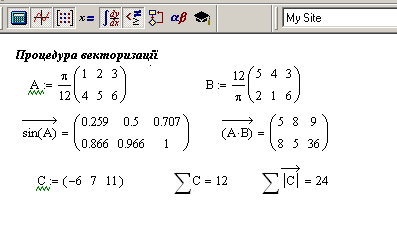
Рис.4.9. Процедура векторизації

4.5. Перетворення масивів

Інколи потрібно мати доступ не до одного елемента масиву, а до його фрагмента, зокрема до рядків чи стовпців масиву.

Для виокремлення в матриці стовпця є оператор на палітрі Мatrix (піктограма з кутовими дужками). Можна також скористатися акордом клавіш <Ctrl> + <6>. У результаті до назви матриці, з якої витягується стовпець, з’являється структурний заповнювач, де вводять верхній індекс. Це число є індексом стовпця матриці, до якого здійснюється доступ, рис.4.10.

Якщо потрібно витягнути рядок з масиву, тоді спочатку матрицю транспонують, а потім звертаються до стовпця транспонованої матриці. Результат буде вектором-стовпцем. Для того, щоб отримати вектор-рядок, одержаний вектор-стовпець треба транспонувати, рис.4.10.

Рис.4.10. Звертання до рядків та стовпців масиву

При потребі додавання рядків чи стовпців матриці, потрібно виокремити елемент матриці. Рядки будуть додаватися під рядком виокремленого елемента, а стовпці додаються праворуч від стовпця цього елемента. Після виокремлення елемента необхідно виконати команду Insert | Matrix. У діалоговому вікні Insert | Matrix в полі Rows вказати число рядків, які необхідно вставити, а полі Сolumns – стовпців та клацнути на кнопці Insert. У результаті отримаємо матрицю змінних розмірів.

Вилучення рядків та стопців виконується практично так само, лише у вікні Insert Matrix слід клацнути не на кнопці Insert, а на кнопці Delete.

Для створення матриць шляхом їх об’єднання застосовують функції stack (А,В) і argument (А,В). Функція stack (А,В) додає матрицю В знизу матриці А, очевидно, що матриця В має мати однакову кількість стовпців з матрицею А.

Функція argument (А,В) додає матрицю В праворуч матриці А, матриці А і В повинні мати однакову кількість рядків.

Функція submatrix (А, n1, n2, m1, m2) дозволяє витягнути під матрицю В з деякої матриці А. Аргументи n1, n2 це початковий і кінцевий рядки під матриці В, які витягуються з матриці А, а аргументи m1, m2 – початкові і кінцеві стовпці підматриці В.

Наприклад: В = submatrix (А, 2, 4, 1.3), тут матриця А хай має розмірність 6 х 6.

Для створення матриці, елементи якої визначаються через індекси, можна скористатися функцією matrix ( ). Функція має три аргументи: перші два – це число рядків і стовпців, потім назва функції, за якою обчислюються елементи матриці, рис.4.11.

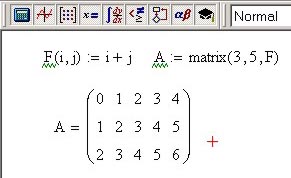
Рис.4.11. Створення матриці з допомогoю функції Matrix ( )

Тут i та j – індекси елемента матриці, за замовчуванням кількість рядків і = 0,1,2,…, М - 1, а стовпців j = 0,1,2,…, N -1.

Деякі функції призначені для визначення розмірів масивів, табл.4.1.

Функція та її аргументи	Опис
Cols (A)	Повертає число стовпців матриці А.
Rows (A)	Повертає число рядків матриці А.
Last (V)	Повертає індекс останнього елемента вектора V.
Length (V)	Повертає число елементів вектора V.

Питання для самоконтролю

1. Яку послідовність дій треба виконати, щоб створити матрицю?

2. Яку послідовність дій треба виконати, щоб створити вектор-стовпець та вектор-рядок ?

3. З якої цифри за замовчуванням починаються індекси елементів масивів ?

4. Як виконати налаштування початкового значення індексу масивів ?

5. Як згенерувати матрицю, елементи якої обчислюються за функціональною залежністю ?

6. Як відобразити значення масиву як матрицю будь-яких розмірів ?

7. Які арифметичні операції над масивами можна проводити? Наведіть приклад.

8. Як знайти обернену матрицю ?

9. Як виконати транспонування матриці ?

10. Як обчислити визначник матриці та векторний добуток?

11. В чому полягає суть векторизації ?

12. Як виокремити стовпець матриці ?

13. Як виокремити рядок матриці ?

14. Яка послідовність дій при додаванні рядків чи стовпців в матрицю ?

15. Яка послідовність дій при вилученні рядків чи стовпців матриці ?

16. Які функції застосовуються при об’єднанні матриць ?

17. Як створювати матрицю з допомогою функції matrix ( ) ?

18. Для чого використовується функція submatrix ( ) ?

ЗАВДАННЯ ДЛЯ ПРАКТИЧНОЇ РОБОТИ №3

Матриці та вектори

Мета роботи. Набути практичні навички зі створення масивів та виведення елементів масивів та виведення елементів масивів при різних значеннях системної змінної ORIGIN. Виконати операції з матрицями та векторами: додавання, множення, зведення до степеня, векторизації, транспонування та знаходження оберненої матриці. Створювати матриці за допомогою функції Matrix ( ), вилучення субматриці. Обчислення векторного та скалярного добутків векторів.

Хід роботи.

1. Сформувати матрицю А та вектор В. Значення елементів матриці та вектора взяти з табл.1.

2. Вивести на екран по два елементи матриці А та вектора В при значеннях системної змінної ORIGIN = 0 та ORIGIN = 1.

3. Транспонувати матрицю А та обчислити обернену матрицю і перемножити обернену матрицю на вихідну.

4. Перетворити вектор-стовпець В на вектор-рядок В1.

5. Виконати звертання до першого та другого стовпців матриці А.

6. Створити матрицю А1, долучивши до матриці А вектор-стовпець В, та матрицю А2, долучивши до матриці А вектор-рядок В1.

7. Створити матрицю А3, елементами якої є значення функції cos( ) від елементів матриці А, при цьому використати процедуру векторизації.

8. Сформувати матрицю Розміром 5 х 6, скориставшись функцією Matrix ( ). Залежність для визначення елементів матриці вибрати самостійно.

9. Вилучити з матриці D під матрицю Е розміром 2 х 3, скориставшись функцією Submatrix ( ).

10. Перемножити матрицю А на матрицю Е, обчислити визначник матриці D, звести матрицю Е до квадрату.

11. Створити вектори В2 та В3, елементами яких є другий та четвертий стовпець матриці D, та обчислити векторний та скалярний добуток цих векторів.