12. Модели вход - состояние - выход. Определение переменных состояния. Векторно-матричная форма записи системы линейных уравнений 1-го порядка.

 , (2.4)

где ^ X – вектор состояния системы;

Y – вектор выходных управляемых величин;

U – вектор внешних воздействий (входных и возмущающих); А, В, С, D – матрицы системы.

Система уравнений (2.4) является стандартным описанием динамических систем в пространстве состояний и представляет собой математическую модель вход-состояние-выход. 

Уравнения (2.4) несут большой объём информации о динамических свойствах системы. Первое уравнение из (2.4) определяет динамические характеристики системы, а второе является уравнением выхода.

Матрица системы A, элементы которой определяются структурной схемой системы и значениями её параметров, характеризует динамические свойства системы, её свободное движение.

Матрица управления B характеризует влияние внешних воздействий на переменные состояния системы, т.е. определяет чувствительность системы к внешним воздействиям (входным и возмущающим).

Матрица наблюдения C характеризует связь выходной величины системы с вектором состояния. Обычно не все составляющие вектора состояния являются наблюдаемыми сигналами, т.е. могут быть измерены с помощью каких-либо датчиков, в то время как выходной сигнал всегда наблюдаем.

Матрица связи D устанавливает связь выходной величины системы с внешним воздействием.

Таким образом, четверка матриц A, B, C, D полностью определяет динамическую систему.

Переменные Состояния определяют состояние или условие математической системы, которая представляет схему в любой момент. Эти переменные должны быть инициализированы к некоторому значению до старта выполненного анализа. 

Векторная форма записи

Система уравнений может быть записана в векторном виде:

A₁x₁ + A₂x₂ + ... + A_nx_n =B

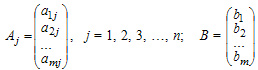
Матричная форма записи

В матричной записи система линейных уравнений может быть записана следующим образом: AX=B

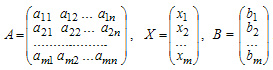
12. Экспериментальные способы построения моделей оу. Задача идентификации. Способы аппроксимации при получении моделей оу.

Если свойства объекта познаны в недостаточной степени, либо про­исходящие явления слишком сложны для аналитического описания, для построения математических моделей реально существующих объектов применяется экспериментальный способ.

Этот способ заключается в активных экспериментах над объектом или в пассивной регистрации его поведения в режиме нормальной эксплуатации (рис. 1.21, а). В результате обработки данных наблюдений получают модели в требуемой форме. Совокупность этих операций объединяется термином «иденти­фикация объекта».

В результате идентификации получаются модели вход-выход  рис. 1.21, б)

Очевидно, модель зависит не только от свойств объекта, но также от входных сигналов, их разнообразия.

Практически об идентифицируемом объекте всегда имеется какая-то априорная информация, т. е. он не является «черным ящиком». Это дает возможность комбинировать оба способа — вначале аналитически строить структуру модели и определять начальные приближенные значения параметров, а далее обработкой экспериментальных данных уточнять их значения.

В ТАУ задачу идентификации рассматривают как задачу отыскания по входным и выходным элементам эквивалентной системы некоторого заданного класса. По результатам получают параметры заданного вида модели – параметрическая идентификация.

Реальные эксперименты выполняются на производстве на этапе пуско-наладочных работ. Поэтому при решении задачи параметрической идентификации возникают проблемы получения информации в условиях помех (фильтрация).

Модели ОУ могут быть детерминированные (функция определена Asin(ωt+φ), стохастические (если A-случайная величина) и адаптивные (идентификация проводится в результате методов, приспосабливающихся к работе системы).

Аппроксимация – научный метод, состоящий в замене одних математических объектов другими в том или ином смысле близкими к исходным, но более простыми (approximo – приближаюсь).

Накопленный инженерный опыт показывает, что при аппроксимации экспериментальных данных аналитическими выражениями в большинстве случаев для объектов, обладающих самовыравниванием, можно ограничиться одним из следующих вариантов описания динамических свойств исследуемых объектов:

1) динамическим звеном второго порядка –

,

,

;

2) динамическим звеном второго порядка с одной постоянной времени –

,

,

;

3) динамическим звеном первого порядка -

; , .

Здесь:

- К -коэффициент передачи; - время запаздывания; Т₀,Т₁,Т₂, T - постоянные времени объекта управления.

Наиболее распространенные способы определения значений постоянных времени следует разделить на: графические и интерполяционные.

Графические способы предполагают нахождение значений постоянных времени с помощью графических построений на полученной кривой разгона.

Интерполяционные способы предполагают нахождение значений постоянных времени в результате пересчета по определенным контрольным точкам переходной характеристики.