6. Задача математического описания аср. Уравнения статики и динамики аср. Примеры получения дифференциальных уравнений систем различной физической природы.

Способы математического описания АСР

Динамические характеристики элементов АСР описываются 2-мя способами:

1) Дифференциальные уравнения

2) Передаточные функции 

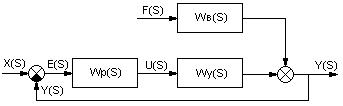
Структурная схема одноконтурной АСР

X(S) - задающее воздействие (задание)

Y(S) - регулируемая величина

E(S) - ошибка регулирования

U(S) - управляющее воздействие (выход регулятора)

F(S) - возмущающее воздействие

Wp(S) - передаточная функция регулятора

Wy(S) - передаточная функция объекта по управляющему воздействию

Wв(S) - передаточная функция объекта по возмущающему воздействию

Для разомкнутой АСР при отсутствии возмущений:

Уравнение динамики: Y(S)=X(S)*Wp(S)*Wy(S)

Уравнение статики (установившийся режим): Y=X*Wp(0)*Wy(0)=X*Kp*Ky

Для замкнутой АСР с возмущениями:

Уравнение динамики:

• относительно регулируемой величины: Y(S)=Фз(S)*X(S)+Фв(S)*F(S),

• относительно ошибки: E(S)=X(S)-Y(S)=Ф_E(S)*X(S)-Фв(S)*F(S),

Уравнение статики:

Y = Фз(0)*X + Фв(0)*F = Kз*X + Kв*F,

E = X - Y = (1-Фз(0))*X - Фв(0)*F = Ф_E(0)*X - Фв(0)*F = Ke*X - Kв*F,

Kз, Ke, Kв - коэффициенты усиления замкнутой АСР по заданию, ошибке и возмущению соответственно, причем Kз + Ke = 1

7. Каноническая и нормальная форма уравнений динамики аср. Задача линеаризации статики аср. Методы исследования динамики аср.

Линеаризация. Обычно автоматические системы описывают нелинейными дифференциальными уравнениями. Но во многих случаях можно их линеаризовать, т. е. заменить исходные нелинейные уравнения линейными, приближенно описывающими процессы в системе. Процесс преобразования нелинейных уравнений в линейные называют линеаризацией.

Каноническая форма:

Каноническая форма представления уравнений состояния зависит от типа корней характеристического уравнения. Особенно удобен такой переход при рассмотрении односвязных систем, не содержащих полиномов в числителе передаточной функции, представлением передаточной функции исследуемой системы в виде суммы элементарных дробей. При комплексных корнях получаются комплексные переменные состояния, и на практике этот случай не применяют.

Рассмотрим случай простых корней. Пусть исследуемая система имеет передаточную функцию вида

Для случая простых и кратных корней

Тогда передаточную функцию можно записать в виде

Представим выходную величину в виде

Система дифференциальных уравнений первого порядка

……………………………………………………….

.

Систему уравнений представим в развернутой матричной форме

,

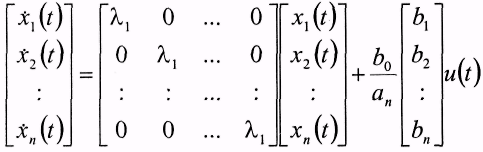или более компактно

здесь x(t) - n-мерный вектор состояния динамической системы,  - диагональная матрица собственных значений размером n*n, b – n-мерный вектор управления. Матрица  связана с матрицей А соотношением

А = Р^-1*А*Р ,

где Р — матрица Вандермонда, а вектор X(t) связан с вектором Z(t) соотношением

X(t) = Р^-1*Z(t).

Нормальная форма:

Линейное дифференциальное уравнение записывают в виде

где a_i и bj — постоянные коэффициенты; р - символ дифференцирования; y(t) - выходная, a u(t) - входная переменные; для реальных систем m<n . Решение этого уравнения ищут для начальных условий

_.

Отношение преобразований Лапласа выходной переменной к входной при нулевых начальных условиях называют передаточной функцией:

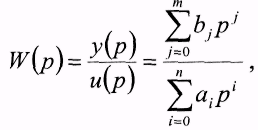
где р - оператор Лапласа.

При b_j = 0 для всех j > 0 и b₀ > < 0 передаточная функция имеет вид

_,

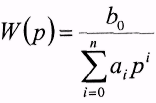а дифференциальное уравнение записывается как

_,

где р — символ дифференцирования.

Выходную переменную y(t) можно получить путем последовательного интегрирования старшей производной pⁿy(t) (рис. 1а). Для этого потребуется n последовательно включенных интеграторов, входы которых представляют собой производные y(t) от pⁿy(t) до py(t). Запись дифференциального уравнения в виде

непосредственно показывает, что высшую производную pⁿy(t) можно получить, умножив выходные переменные интеграторов на соответствующие коэффициенты от а_n-1 до a₀, просуммировав результаты, вычтя эту сумму из переменной b_ou(t) и, наконец, умножив полученную таким образом переменную на коэффициент 1/а_n (рис. 1б).

Обозначив y(t) = z₁(t), py(t)=z₂(t) и т.д. до p^n-]y(t) = z_n(t), записываем дифференциальное уравнение n-го порядка (5) как систему n дифференциальных уравнений первого порядка:

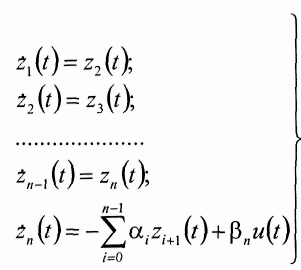
с начальными условиями z_i(o) = y_i0; где и .

В матричной форме систему уравнений (7) в развернутом виде записывают как

_,

или сокращенно как

,

где Z(t) = [z1(t), z2(t), zn(t)] - n - мерный вектор состояния; А — квадратная матрица размера n*n и  = [0,0,...,0, n] - вектор-столбец управления.

Исследование динамической системы сводится к решению дифференциальных уравнений:

• Классическим методом

• Методом преобразований Лапласа

• Методом вычетов