12. Показатели качества промышленных систем управления. Прямые и косвенные показатели качества.

Качество САУ определяется следующими показателями:

1. Время достижения установившегося режима – такое время, по истечении которого для управляемой величины выполняется условие:

,

г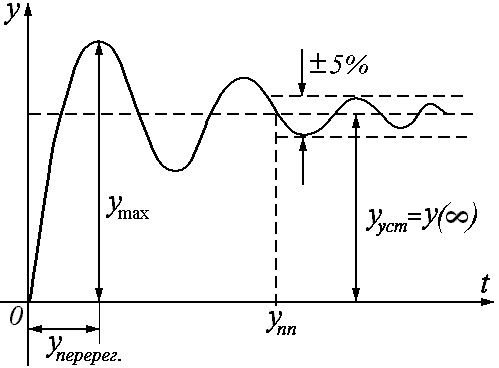 де у – управляемая величина; _р – некоторая величина (для САУ 5% от установившегося режима).

Время переходного процесса – отрицательное время, при котором переходный процесс по выходной координате достигает 5%-ной зоны от устойчивого значения.

2. Перерегулирование - это процентное соотношение разницы максимального перерегулирования и установившегося значения:

.

2. а) Время максимального перерегулирования (t_{перерег}), такое время, при котором выходная величина достигает своего максимального по модулю значения:

.

2. б) Число перерегулирований – это количество раз, когда управляемая величина превышает по модулю значение:

.

3. Колебательность () - кол-во колебаний, приходящихся на отрезок времени переходного процесса.

4. Ошибка в установившемся режиме (точность САУ)

.

Д

ля статических систем ошибку можно графически продемонстрировать как:

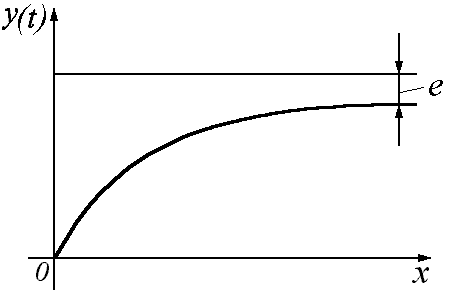
Для астатических систем:

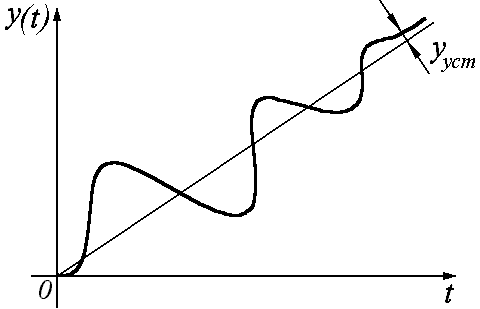
Первые два показателя – это показатели качества переходного процесса, а четвертый – показатель качества в установившемся режиме. Вместе они образуют группу показателей качества САУ.

Для анализа показаний качества управления могут быть использованы прямые и косвенные методы оценки.

Прямые методы определения качества базируются на исследовании переходного процесса, дают наиболее достоверную информацию с последующим определением показаний качества. Но они являются самыми трудоемкими.

Косвенные методы определения качества позволяют по косвенным признакам, не решая ни дифференциальных, ни характеристических уравнений, получить приближенный переходный процесс с приближенными показателями качества.

Прямые методы оценки качества:

• Классический метод;

• Операторный метод;

• Частотный метод;

• Моделирование на ЭВМ.

12. Определение запаса устойчивости. Понятие доминирующей компоненты в переходном процессе. Корневые оценки запаса устойчивости. Расширенная частотная характеристика. Обобщенный критерий Найквиста - Дудникова.

В условиях эксплуатации параметры системы по тем или иным причинам могут меняться в определенных пределах (старение, температурные колебания и т.п.). Эти колебания параметров могут привести к потере устойчивости системы, если она работает вблизи границы устойчивости. Поэтому стремятся спроектировать САУ так, чтобы она работала вдали от границы устойчивости. Степень этого удаления называют запасом устойчивости.

Согласно критерия Найквиста, чем дальше АФЧХ от критической точки (-1, j0), тем больше запас устойчивости. Различают запасы устойчивости по модулю и по фазе.

^ Запас устойчивости по модулю характеризует удаление годографа АФЧХ разомкнутой САУ от критической точки в направлении вещественной оси и определяется расстоянием h от критической точки до точки пересечения годографом оси абсцисс.

^ Запас устойчивости по фазе характеризует удаление годографа от критической точки по дуге окружности единичного радиуса и определяется углом  между отрицательным направлением вещественной полуоси и лучом, проведенным из начала координат в точку пересечения годографа с единичной окружностью.

Запас устойчивости в линейных системах можно задать двумя способами:

1. Задать распределение корней характеристического уравнения

2. Задать определенные требования частотным характеристикам системы

Корневая оценка запаса устойчивости характеризует, насколько можно изменять корни характеристического уравнения без потери системой устойчивости.

в качестве оценки устойчивости используем величину:

которая может изменяться в диапазоне  . Чем меньше ω (то есть больше мнимая часть корня), тем ближе система к границе устойчивости. При  она находится на границе устойчивости, если же ω=∞, система будет абсолютно устойчива.

Известна передаточная функция разомкнутой системы

(4.25)

Здесь   - ее характеристический полином.

Структурная схема замкнутой системы имеет вид:

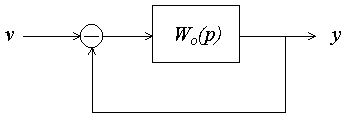
Рис.4.15. Структурная схема замкнутой системы

Передаточная функция замкнутой системы следующая:

,

(4.26)

где   - характеристический полином замкнутой системы.

Для получения критерия устойчивости вводится вспомогательная функция:

(4.27)

Как видим, числитель вспомогательной передаточной функции представляет собой характеристический полином замкнутой системы, а знаменатель - характеристический полином разомкнутой системы. Так как   то в выражении для A(p) порядок суммы полиномов равен  . Следовательно, во вспомогательной передаточной функции   полиномы числителя и знаменателя имеют одинаковый порядок ( n).

В выражении (4.27) заменим p на   и получим:

(4.28)

Рассмотрим результирующий угол поворота вектора   при изменении   от 0 до  , используя те же соотношения, что и при доказательстве критерия Михайлова.

Если замкнутая система устойчивая, то общее приращение фазы числителя (4.28) будет равно

(4.29)

При устойчивой разомкнутой системе фаза знаменателя

(4.30)

Результирующий угол поворота вектора   равен разности (4.29) и (4.30)

(4.31)

Таким образом, для устойчивости замкнутой системы при устойчивой разомкнутой должно выполняться соотношение (4.31). Это свойство имеет простую геометрическую интерпретацию: вспомогательная частотная характеристика не должна охватывать начало координат. Так как  отличается от   на единицу, то можно строить амплитудно - фазовую характеристику разомкнутой системы, что значительно проще.

Формулировка критерия Найквиста: для устойчивости замкнутой системы необходимо и достаточно чтобы амплитудно - фазовая характеристика устойчивой разомкнутой системы при изменении   от0 до   не охватывала точку с координатами {-1, j0}.

Расширенные частотные характеристики получаются заменой:

Система, имеющая в разомкнутом состоянии корневой показатель колебательности не ниже m, сохраняет его и после колебания, если расширенная частотная характеристика не охватывает опасную точку.

12. Определение запаса устойчивости. Оценка запаса устойчивости по частотному показателю колебательности. Гипотеза об эквивалентности свойств колебательного звена и обычной системы регулирования. Диаграмма Холла.

В условиях эксплуатации параметры системы по тем или иным причинам могут меняться в определенных пределах (старение, температурные колебания и т.п.). Эти колебания параметров могут привести к потере устойчивости системы, если она работает вблизи границы устойчивости. Поэтому стремятся спроектировать САУ так, чтобы она работала вдали от границы устойчивости. Степень этого удаления называют запасом устойчивости.

Согласно критерия Найквиста, чем дальше АФЧХ от критической точки (-1, j0), тем больше запас устойчивости. Различают запасы устойчивости по модулю и по фазе.

^ Запас устойчивости по модулю характеризует удаление годографа АФЧХ разомкнутой САУ от критической точки в направлении вещественной оси и определяется расстоянием h от критической точки до точки пересечения годографом оси абсцисс.

^ Запас устойчивости по фазе характеризует удаление годографа от критической точки по дуге окружности единичного радиуса и определяется углом  между отрицательным направлением вещественной полуоси и лучом, проведенным из начала координат в точку пересечения годографа с единичной окружностью.

Запас устойчивости в линейных системах можно задать двумя способами:

3. Задать распределение корней характеристического уравнения

4. Задать определенные требования частотным характеристикам системы

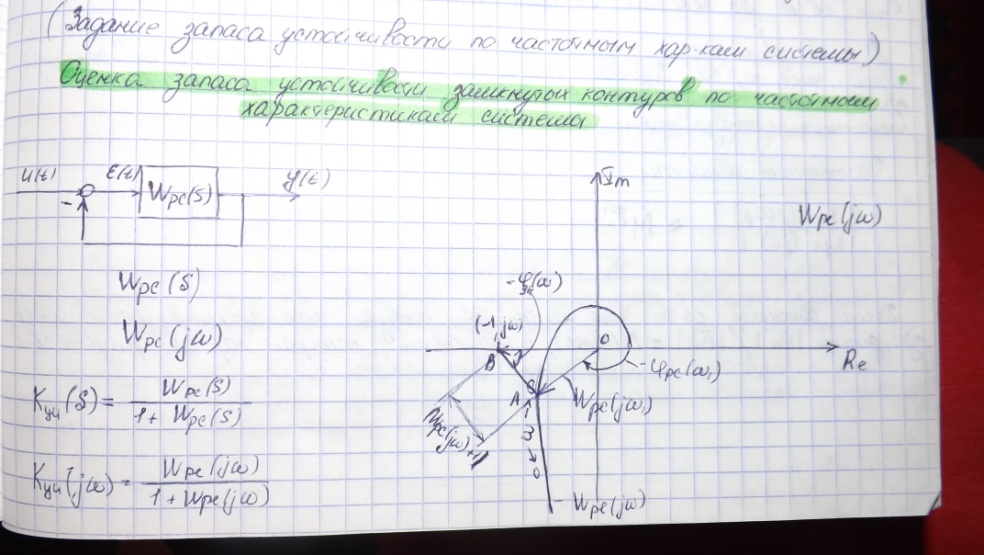
Оценка запаса устойчивости по частотному показателю колебательности:

По критерию Найквиста эта нейтральная система, устойчивая в разомкнутом состоянии, будет устойчива, т.к. не охватывает критическую точку.

Максимум частотной характеристики замкнутой системы становится бесконечным.

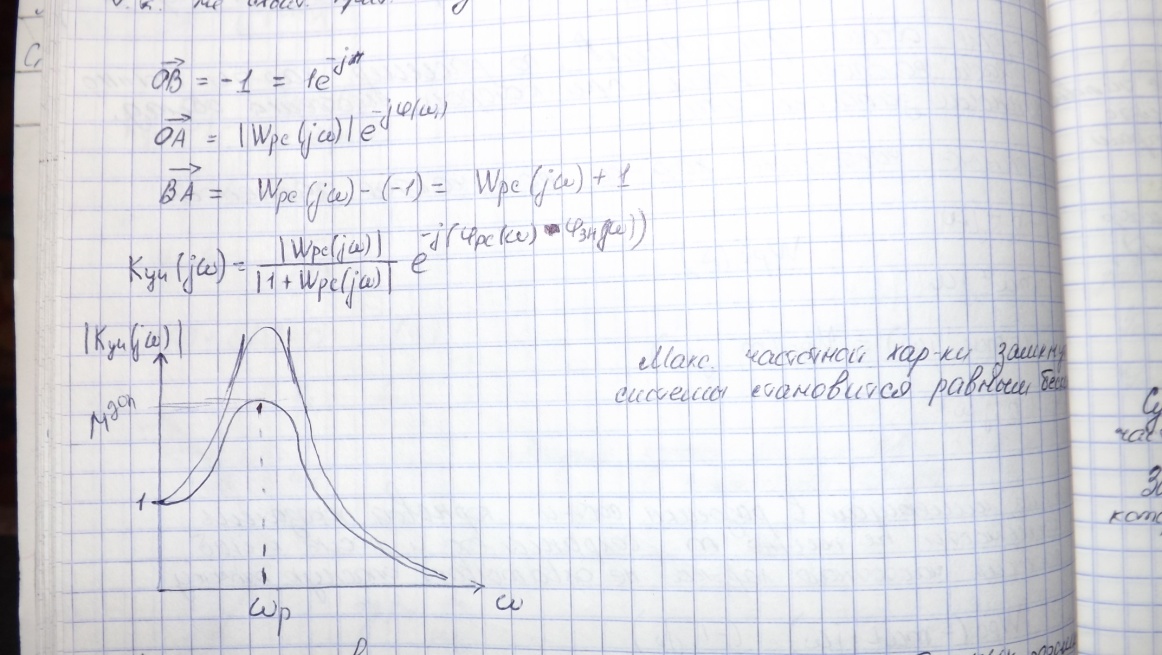Предложим задавать запас устойчивости таким образом, чтобы КЧХ разомкнутой системы проходила достаточно далеко от опасной точки, т.е. запас оценить величиной максимальной:

- частотный показатель колебательности ЗС. , при 1

Гипотеза об эквивалентности свойств колебательного звена и обычной системы регулирования: приведенная частотная характеристика замкнутой системы идентична частотной характеристике колебательного звена, поэтому при решении задач параметрического синтеза предполагают, что свойства замкнутой системы эквивалентны свойствам колебательного звена.

В колебательном звене существует однозначная зависимость между расколочением корней и параметров частотной характеристики. Задавая запас устойчивости по корневым показателям, при выполнении гипотезы об эквивалентности, определяется и запас устойчивости по частотным показателям.

Частотные области:

Диаграмма Холла: Холл, рассматривая свойства частотной характеристики ЗС, показал, что геометрическое место точек, где , является окружностью.

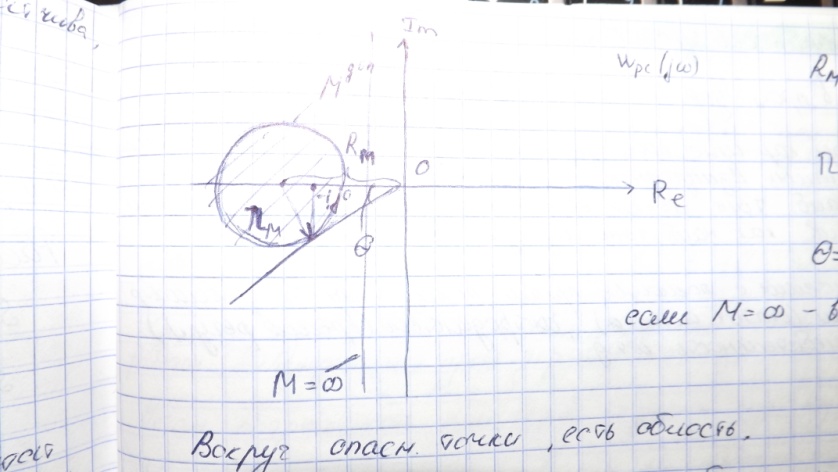Вокруг опасной точки есть область. Если М=∞, то выражается в прямую.

; ; ;

Существуют Диаграммы Холла для того, чтобы по частотной характеристики разомкнутой системы строить частотные характеристики замкнутой системы.

Задавая М, определяют следующие требования к запасу устойчивости: запас устойчивости по модулю и запас устойчивости по фазе.

С-запас устойчивости по модулю

γ- запас устойчивости по фазе

Физически запас устойчивости по модулю означает насколько можно изменить коэффициент усиления в разомкнутой системе, чтобы замкнутая система стала неустойчива

Запас устойчивости по фазе показывает значение изменения фазы в разомкнутой системе, когда она становится неустойчивой.