12. Принцип аргумента: Критерий устойчивости Михайлова.

Позволяют судить об устойчивости САР по виду ее ЧХ. Наиболее распространенные – критерии Михайлова, Найквиста. Более изящным является критерий Найквиста, который используется для исследования устойчивости замкнутых САР, судя о ней по виду известной ЧХ разомкнутой системы.

Все частотные критерии устойчивости базируются на принципе аргумента.

Принцип аргумента

Рассмотрим полином с действительными коэффициентами

,

имеющий n нулей, среди которых m являются правыми (имеют положительную вещественную часть), а остальные n–m – левыми.

Теорема. Приращение аргумента вектора при изменении частоты w от –¥ до +¥ равно разности между числом левых и правых нулей полинома , умноженной на p. т.е.

,

где – общее число нулей (равное порядку полинома ); – число правых нулей.

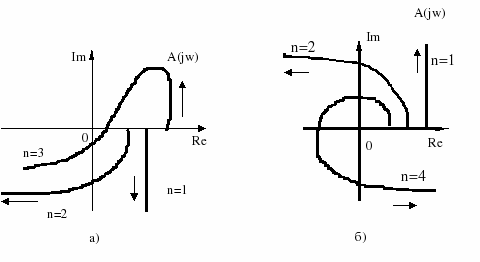
Примеры годографов Михайлова – а) неустойчивых систем; б) устойчивых систем.

Формулировка критерия Михайлова: 

Для устойчивости линейной системы автоматического управления необходимо и достаточно, чтобы годограф Михайлова, начинаясь на действительной, положительной полуоси при изменении  от 0 до , последовательно, в положительном направлении (против часовой стрелки) обходил n квадрантов, где n- порядок характеристического уравнения.

12. Критерий устойчивости Найквиста. Применение критерия Найквиста при оценке влияния свойств отдельных элементов системы на устойчивость.

Критерий Найквиста позволяет судить об устойчивости замкнутой системы по частотному годографу разомкнутой системы. Поскольку частотный годограф может быть построен на основании результатов измерений, то это единственный критерий позволяющий использовать экспериментальные данные.

Разомкнутая система может находиться в одном из трех состояний: устойчивая, неустойчивая и нейтральная. Рассмотрим эти состояния более подробно.

1. Разомкнутая система находится в устойчивом состоянии.

Формулировка критерия Найквиста для этого случая принимает следующий вид:

^ Для устойчивости замкнутой системы необходимо и достаточно, чтобы частотный годограф р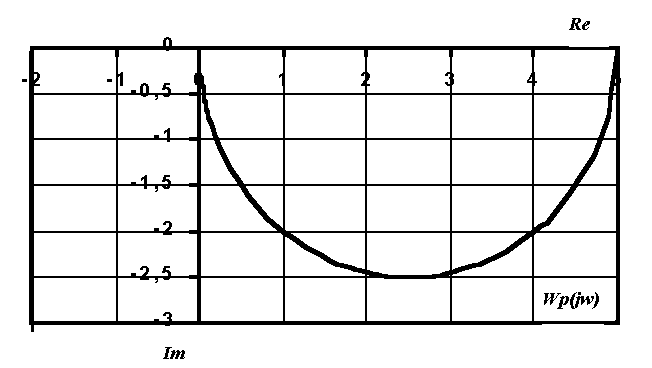 азомкнутой системы при изменении частоты от 0 до  не охватывал точку (-1;0).

Пример частотного годографа, построенный для разомкнутой системы, у которой  ,

(k=10, T=0.5) Стрелкой показано направление увеличения частоты.

Поскольку годограф на рис. 5.5 не охватывает точку –1,0, то замкнутая система будет устойчивой.

Р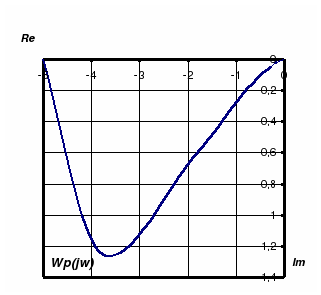 азомкнутая система неустойчива.

Формулировка критерия Найквиста для этого случая принимает следующий вид: 

^ Для устойчивости замкнутой системы необходимо и достаточно, чтобы частотный годограф разомкнутой системы при изменении частоты от 0 до  охватывал точку (-1;0) L/2 раз, где L - количество корней характеристического уравнения, принадлежащих правой части комплексной п лоскости.

Рис. 5.6. Частотный годограф разомкнутой системы, для а) L=1; б) L=2.

На рис. 5.6,а представлен частотный годограф неустойчивой разомкнутой системы ( ), которая имеет один корень характеристического уравнения в правой части. Стрелка показывает направление увеличения частоты. Видно, что годограф ½ раза охватывает точку –1,0, что свидетельствует об устойчивости замкнутой системы. Читателю предлагается в качестве упражнения, проверить это утверждение с помощью других рассмотренных выше критериев.

На рис. 5.6,б представлен частотный годограф неустойчивой разомкнутой системы ( ), которая имеет два корня характеристического уравнения в правой части комплексной плоскости. Видно, что годограф ½ раза охватил точку –1,0, в то время как L/2=1. Вывод - замкнутая система будет неустойчивой.