12. Основы структурного метода анализа систем управления. Понятие графа. Граф структурной схемы. Сигнальные графы. Формула Мэйсона.

Исследование Систем Управления - процесс определения орг. структуры (состава, организации, поведения, состояния систем), параметров системы, закономерностей функционирования и развития изучаемой системы с целью ее совершенствования.

Общая интегральная задача ИСУ - изучение закономерностей функционирования и развития СУ => функциональные задачи:

1. сбор и обработка информации о системе управления

2. оценка и анализ состояния, поведения и параметров СУ

3. характеристика орг. структуры СУ

4. анализ функционирования и развития подсистем СУ

5. характеристика экономических и социальных последствий развития СУ

Структура СУ – причинно-следственные связи между элементами направленного действия. Структуру строят как соотношения на множествах. Формально отношения между множествами называют графами.

Граф — это совокупность непустого множества вершин и набором пар вершин (связей между вершинами).

Объекты представляются как вершины, или узлы графа, а связи — как дуги, или рёбра.

Для разных областей применения виды графов могут различаться направленностью, ограничениями на количество связей и дополнительными данными о вершинах или рёбрах.

Систему, связывающую множество входов с множеством выходов, принято называть бинарным графом. Графы являются универсальным средством описания структуры системы. При небольшом количестве элементов и связей между элементами наглядными являются диаграммы графов и геометрические образы.

В зависимости от элементов множеств рассматривают различные типы графов. В теории управления широко используют понятие структурной схемы. Существуют типовые структуры, которые отражают типовые формы связи между элементами, если изображается это в виде диаграмм, то говорят, что структурная схема – это ориентированный граф.

В зависимости от подхода к моделированию различают структурные модели с раскрытой структурой и нераскрытой. Структура модели с раскрытой структурой представляет собой структурную схему (С-граф) или сигнальный граф (граф Мейсона).

Сигнальный граф – представляет собой удобную форму изображения структурной схемы в виде соотношения множеств дуг и вершин, где переменные системы определяют вершины, а дуги – это передаточная функция, т.е. сигнальные граф – обратный С-графу.

12. Характеристики систем с типовой структурой (алгебра передаточных функций).

Структурную схему составляют на основании функциональной схемы, и для каждого элемента функциональной схемы записывают уравнения, исходя из физических законов, которым подчиняются процессы в нем.

Описание системы просто получить, если оперировать передаточными функциями звеньев.

Рассмотрим основные правила преобразования структурных схем.

1. Передаточная функция цепочки последовательно соединенных звеньев направленного действия.

Рис. 3.12. Структурная схема последовательно соединенных звеньев

Система уравнений в этом случае.

x₂(t)=x₁(t)*W₁(p),

x₃(t)=x₂(t)*W₂(p),

y(t)=x₃(t)*W₃(p).

Исключив из этой системы промежуточные переменные, получим y(t)=x₁(t)*[W₁(p)*W₂(p)*W₃(p)].

Отсюда:  ,

передаточная функция цепочки последовательно соединенных звеньев равна произведению передаточных функций отдельных звеньев.

2. Параллельное соединение звеньев.

Рис. 3.13. Структурная схема параллельно соединенных звеньев

При таком соединении на вход всех звеньев подается один и тот же сигнал, а выходные величины складываются. Цепь из параллельно соединенных звеньев можно заменить одним звеном с передаточной функцией W(p). Из определения передаточной функции следует:

y₁(t)=x(t)*W₁(p)

y₂(t)=x(t)*W₂(p)

y₃(t)=x(t)*W₃(p).

Сложив переменные, получим y(t)=x(t)*[W₁(p)+W₂(p)+W₃(p)],

,

т.е. передаточная функция группы параллельно соединенных звеньев равна сумме передаточных функций отдельных звеньев.

3. Звено, охваченное обратной связью.

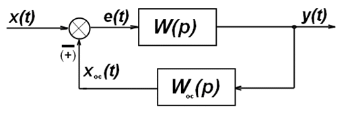
Рис. 3.14. Структурная схема звена, охваченного обратной связью

Обратная связь чаще всего может быть отрицательной, когда e(t)=x(t)-x_ос(t). Если разомкнуть обратную связь перед сравнивающим звеном, то получим цепь из двух последовательно соединенных звеньев, передаточную функцию этой цепи назовем главной: W_гл(p)=W(p)*W_ос(p).

Определим передаточную функцию замкнутой цепи – Ф(p)= . Схема (рис. 3.14) описывается уравнениями:

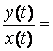Ф .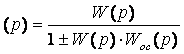

Плюс в знаменателе передаточной функции замкнутой системы соответствует отрицательной обратной связи.

Таким образом, передаточная функция звена, охваченного отрицательной обратной связью, равна передаточной функции прямой цепи – W(p), деленной на единицу плюс передаточная функция разомкнутой цепи ( W_гл(p) ). В рассмотренных выше выражениях   - оператор дифференцирования.

12. Определение типового линейного звена АСР. Свойства типовых линейных звеньев АСР (усилительного, инерционного, интегрирующего, дифференцирующего, реального дифференцирующего, интегро - дифференцирующего, колебательного, запаздывающего).

Звеном системы называется ее элемент, обладающий определенными свойствами в динамическом отношении. Звенья систем регулирования могут иметь разную физическую природу (электрические, пневматические, механические и др. звенья), но описываться одинаковыми ДУ, а соотношение входных и выходных сигналов в звеньях описываться одинаковыми передаточными функциями.

В ТАУ выделяют группу простейших звеньев, которые принято называть типовыми. Статические и динамические характеристики типовых звеньев изучены достаточно полно. Типовые звенья широко используются при определении динамических характеристик объектов управления. Например, зная переходную характеристику, построенную с помощью самопишущего прибора, часто можно определить, к какому типу звеньев относится объект управления, а следовательно, его передаточную функцию, дифференциальное уравнение и т.д., т.е. модель объекта. Типовые звенья Любое сложное звено может быть представлено как соединение простейших звеньев.

К простейшим типовым звеньям относятся:

• усилительное,

• инерционное (апериодическое 1-го порядка),

• интегрирующие (реальное и идеальное),

• дифференцирующие (реальное и идеальное),

• апериодическое 2-го порядка,

• колебательное,

• запаздывающее.

1) Усилительное звено.

Звено усиливает входной сигнал в К раз. Уравнение звена у = К*х, передаточная функция W(s) = К. Параметр К называется коэффициентом усиления.

Выходной сигнал такого звена в точности повторяет входной сигнал, усиленный в К раз.

у = K^.x.

При ступенчатом воздействии h(t) = K.

Примерами таких звеньев являются: механические передачи, датчики, безынерционные усилители и др.

2) Интегрирующее.

2.1) Идеальное интегрирующее.

Выходная величина идеального интегрирующего звена пропорциональна интегралу входной величины:

; W(s) =

При подаче на вход звена ступенчатого воздействия x(t) = 1 выходной сигнал постоянно возрастает:

h(t) = K^.t.

Это звено астатическое, т.е. не имеет установившегося режима.

Примером такого звена может служить емкость, наполняемая жидкостью. Входной параметр – расход поступающей жидкости, выходной - уровень. Изначально емкость пуста и при отсутствии расхода уровень равен нулю, но если включить подачу жидкости, уровень начинает равномерно увеличиваться.

2 .2) Реальное интегрирующее.

Передаточная функция этого звена имеет вид

W(s) = .

Переходная характеристика в отличие от идеального звена является кривой:

h(t) = K^.(t – T) + K^.T^.e ^-t/T.

Примером интегрирующего звена является двигатель постоянного тока с независимым возбуждением, если в качестве входного воздействия принять напряжение питания статора, а выходного - угол поворота ротора. Если напряжение на двигатель не подается, то ротор не двигается и угол его поворота можно принять равным нулю. При подаче напряжения ротор начинает раскручиваться, а угол его поворота сначала медленно вследствие инерции, а затем быстрее увеличиваться до достижения определенной скорости вращения.

3) Дифференцирующее.

3.1) Идеальное дифференцирующее.

Выходная величина пропорциональна производной по времени от входной:

; W(s) = K*s

При ступенчатом входном сигнале выходной сигнал представляет собой импульс (-функцию): h(t) = K^.(t).

3.2) Реальное дифференцирующее.

Идеальные дифференцирующие звенья физически не реализуемы. Большинство объектов, которые представляют собой дифференцирующие звенья, относятся к реальным дифференцирующим звеньям, передаточные функции которых имеют вид

W(s) = .

Переходная характеристика: .

Пример звена: электрогенератор. Входной параметр – угол поворота ротора, выходной – напряжение. Если ротор повернуть на некоторый угол, то на клеммах появится напряжение, но если ротор далее не вращать, напряжение снизится до нуля. Резко упасть оно не может вследствие наличия индуктивности у обмотки.

4) Инерционное 1-ого прядка (апериодическое).

Этому звену соответствуют ДУ и ПФ вида

; W(s) = .

Определим характер изменения выходной величины этого звена при подаче на вход ступенчатого воздействия величины х₀.

h(t) = K(1 - ).

Постоянная Т называется постоянной времени.

Большинство тепловых объектов являются апериодическими звеньями. Например, при подаче на вход электрической печи напряжения ее температура будет изменяться по аналогичному закону.

5) Инерционные звенья 2-ого порядка

Звенья имеют ДУ и ПФ вида

,

W(s) = .

При подаче на вход ступенчатого воздействия амплитудой х₀ переходная кривая будет иметь один из двух видов: апериодический (при Т₁  2Т₂) или колебательный (при Т₁  < 2Т₂).

В связи с этим выделяют звенья второго порядка:

• апериодическое 2-го порядка (Т₁  2Т₂),

• колебательное (Т₁  < 2Т₂),

• консервативное (Т₁ = 0).

6) Запаздывающее.

Если при подаче на вход объекта некоторого сигнала он реагирует на этот сигнал не моментально, а спустя некоторое время, то говорят, что объект обладает запаздыванием.

Запаздывание – это интервал времени от момента изменения входного сигнала до начала изменения выходного.

Запаздывающее звено – это звено, у которого выходная величина у в точности повторяет входную величину х с некоторым запаздыванием :

y(t) = x(t - ).

Передаточная функция звена:

W(s) = e^-s. h(t) = 1(t - ).

Примеры запаздываний: движение жидкости по трубопроводу (сколько жидкости было закачано в начале трубопровода, столько ее выйдет в конце, но через некоторое время, пока жидкость движется по трубе), движение груза по конвейеру (запаздывание определяется длиной конвейера и скоростью движения ленты) и т.д.