5. Синтез линейных систем управления

5.1.Основные понятия

Формулировка задачи синтеза. Проблема синтеза занимает центральное место в теории автоматического управления, так как наличие адекватных способов расчета определяет успех проектирования реальных систем управления. С момента зарождения автоматики как науки этой проблеме уделялось особое внимание: уже в первых работах Д. Максвелла и И.А. Вышнеградского предлагались рекомендации по вы­бору численных значений отдельных параметров регуляторов. Однако регулярные методы синтеза появились вместе с применением частотных характеристик для исследования систем автоматического регулирования.

В настоящее время частотный метод считается классическим и остается одним из основных при расчете линейных систем. Широкое применение этого метода и различных его модификаций обусловлено еще и тем, что он дает приемлемые результаты даже при небольшом изменении параметров модели реального объекта.

Во второй половине XX века появились новые методы синтеза, которые принято называть современными. Некоторые из них основаны на использовании модальных (корневых) характеристик систем. Они в большей степени зависят от параметров модели, чем классические.

Частотные методы удобно использовать для режима отработки входных воздействий, а модальные – при проектировании систем, режим работы которых предполагает отработку возмущений и начальных условий.

В настоящее время для синтеза линейных систем разработано около 15 методов. Однако наибольшее распространение из них получили 5-6.

Под синтезом будем понимать проектирование регулятора для системы автоматического управления по заданным требованиям к динамическим и статическим свойствам последней.

Правильно поставленная задача синтеза должна содержать три элемента:

1.Задание математической модели объекта.

2.Задание требований к статическим и динамическим свойствам системы.

3.Задание класса регуляторов.

Математическая модель объекта, как известно, может быть представлена в виде:

 системы дифференциальных уравнений (математическая модель описывается тройкой матриц );

 передаточных функций (матриц) ;

 частотных характеристик системы .

В зависимости от выбранной формы описания объекта, требования к статике и динамике системы могут быть сформулированы в виде:

 желаемых матриц , задающих поведение замкнутой системы;

 желаемых передаточных функций (матриц) замкнутой системы ;

 желаемых частотных характеристик замкнутой системы .

Желаемые характеристики во всех трёх случаях определяются исходя из требуемых показателей качества переходного процесса, т.е. .

Класс регуляторов задаётся также в зависимости от выбора описания объекта.

Сочетание всех трёх элементов обуславливает выбор метода синтеза системы. При синтезе современных сложных систем управления необходимо проводить анализ с точки зрения их управляемости, а предъявляемых требований – с точки зрения их реализуемости.

Выбор метода синтеза определяется технической ситуацией, поэтому целесообразно предварительно классифицировать режимы работы системы, модель которой имеет вид

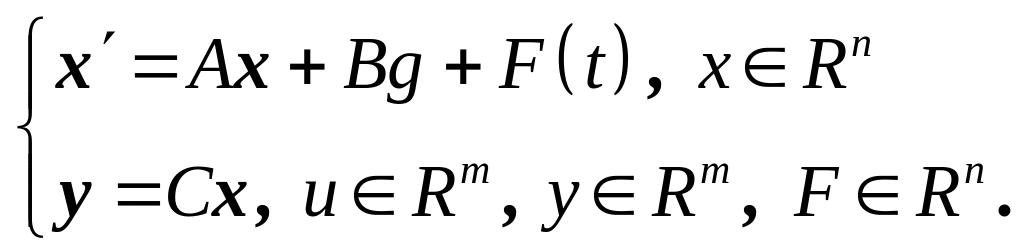(5.1)

Процессы в ней описываются соотношением

(5.2)

Они обусловлены различными факторами: ненулевыми начальными условиями, входными воздействиями и возмущениями. Обычно в системе протекают смешанные процессы, однако для расчета регулятора их удобно различать, поэтому выделим основные режимы работы.

Режимом отработки начальных условий будем называть процесс перехода из произвольных начальных состояний в равновесные при отсутствии внешних воздействий на систему (рис. 5.1, а). Первую составляющую выражения (5.2), которая определяет этот режим работы, называют свободной составляющей процесса.

Рис. 5.1. Иллюстрация режимов отработки

а – начальных условий, б – входа

Режимом отработки входа (см. рис. 5.1, б) будем называть процесс отработки входного воздействия, когда . Такому режиму работы соответствует вторая составляющая выражения (5.2).

Режимом слежения за входом будем называть процесс отработки изменяющегося входного воздействия при нулевых начальных условиях и отсутствии возмущений . Данному процессу также будет соответствовать вторая составляющая выражения (5.2).

Режимом отработки возмущений будем называть процессы, вызванные в системе возмущением при фиксированных начальных условиях и . Третья составляющая выражения (5.2) отражает процесс отработки возмущения.

Выбор метода синтеза обусловлен режимом работы системы, причем требования к качеству процессов задаются в определенной форме на основе стандартных оценок: быстродействия, перерегулирования и статической ошибки.

При отработке входа для описания процессов обычно используются следующие динамические характеристики: h(t), w(t), W(p), W(jω), которым соответствуют определенные методы синтеза. К настоящему времени наиболее полно разработан частотный метод, основанный на логарифмических частотных характеристиках L(ω) и φ(ω). Если рассматривается режим отработки начальных условий и возмущений, то лучше применять модальный метод синтеза.