От вида корней характеристического полинома
В этом случае получаются затухающие синусоидальные колебания
(рис.
4.3, б),
причем мнимая часть
есть круговая частота колебаний, а
– показатель затухания. При положительных
вещественных частях корней процесс
представляет собой расходящиеся
синусоидальные колебания (рис. 4.3, в).
3. Чисто мнимые корни. Для двух сопряженных мнимых корней составляющая переходного процесса определяется выражением
.
Такой процесс представляет собой незатухающие колебания, показанные на рис. 4.3, г.
Свободные движения. Преобразуем дифференциальное уравнение (4.2) по Лапласу с учетом начальных условий:
.
(4.5)
Изображение решения уравнения (4.2) следует из (4.5)
.
Если
полином
имеет только простые корни pi,
i
= 1,…, n,
то выражение для свободных движений
есть
,
(4.6)
где
(′) – символ дифференцирования полинома
по p,
а
− вычет.
Если же корни полинома – кратные, то вместо Ci в (4.6) появятся полиномы от t со степенями ниже кратности K корня pj
.
Таким образом, для того, чтобы свободная составляющая была затухающей, необходимо чтобы корни были либо вещественными отрицательными или комплексными с отрицательными вещественными частями
,
т.е. все корни должны находиться левее мнимой оси. Это же условие имеет место и для собственных значений матрицы состояний A.
Таким образом, система устойчива по входу-выходу, если:
− система устойчива по начальным условиям, т.е. ее корни, находятся в левой полуплоскости;
− передаточная функция системы физически реализуема, т.е. в ней степень полинома числителя n не превышает степени полинома знаменателя m.
Критерии устойчивости. Выявление устойчивости возможно не только путем определения значений коней полиномов, но и на основе критериев устойчивости, позволяющих с помощью относительно простых вычислений определить, лежат ли все корни в левой полуплоскости. Различают алгебраические (Гурвица и Рауса) и частотные (Найквиста и Михайлова) критерии.
Алгебраические критерии основаны на исследовании зависимостей между видом корней характеристического полинома и значениями коэффициентов полинома при неизвестных. Это позволяет свести задачу исследования системы, описываемой дифференциальным уравнением, к выполнению алгебраических преобразований для нахождения условий, которым должны удовлетворять коэффициенты полинома. Такие условия были найдены в 1877 г. Е. Раусом. Другая форма этих условий была найдена в 1895 г. А. Гурвицем. Суть их заключается в следующем: для того чтобы характеристический полином имел корни только с отрицательными действительными частями, необходимо, чтобы его коэффициенты имели один и тот же знак.
Критерий Рауса. Пусть характеристический полином звена или системы имеет противоположную обычной записи индексацию коэффициентов
.
Образуем из его коэффициентов матрицу размерности
вида
,
(4.7)
где
– целочисленный остаток от деления n
на 2 (значение четности n),
элементы двух нижних строк (4.7) есть
коэффициенты полинома
,
элементы
следующих двух строк определяются
формулами
,
.
Элементы
следующих двух строк определяются этими
же формулами, в которых элементы a
и b
заменены соответственно элементами b
и c.
Раус
доказал, что для отрицательности
действительных частей корней полинома
необходимо и достаточно, чтобы все
элементы первого столбца матрицы (4.7)
были положительными:
.
Пример 4.2. Определить условия устойчивости для систем 1 ÷ 4 порядка.
Решение. Для уравнения первого порядка
матрица Рауса имеет вид
,
величины
и
равны нулю и условия устойчивости
сводятся к
.
Это условие является необходимым и
достаточным.
Для уравнения второго порядка
матрица Рауса имеет вид
,
где
,
а
остальные величины
и
равны нулю и условия устойчивости
сводятся к
.
Это условие также является необходимым
и достаточным.
Для уравнения третьего порядка
(4.6)
матрица Рауса имеет вид
,
где
,
,
т.е.
вычисляются элементы
и
,
а остальные вели-
чины и равны нулю и условия устойчивости в этом случае принимают вид
,
т.е. здесь условие положительности коэффициентов полинома необходимо, но не достаточно.
Для уравнения четвертого порядка
матрица Рауса имеет вид
,
где
,
,
,
,
т.е.
вычисляются элементы
,
,
,
,
а остальные величины
и
равны нулю и условия устойчивости в
этом случае принимают вид:
.
▄
Пример 4.3. Для системы, описываемой передаточной функцией с характеристическим полиномом
,
(4.8)
определить, является ли она устойчивой.
Решение. Таблица Рауса для этой системы выглядит так:
,
так как
,
,
,
.
Поскольку
один из элементов первого столбца
матрицы Рауса отрицателен, система
неустойчива. Заметим, что система с
характеристическим уравнением вида
(4.8) неустойчива при любом
.
▄
Критерий Гурвица. Из коэффициентов характеристического полинома , представленного в виде
, (4.9)
либо – в виде
составляются матрицы Гурвица вида
или
,
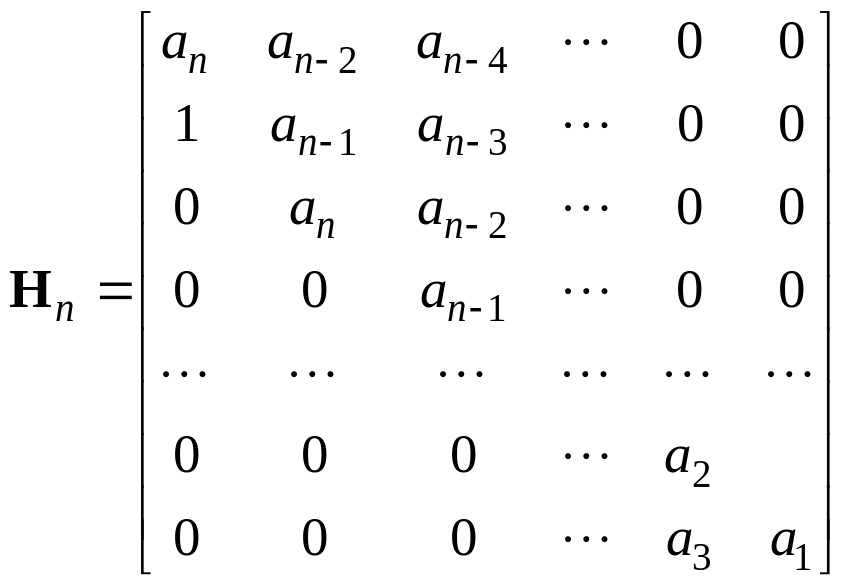представляющие собой квадратные матрицы размера nn. Их диагональными определителями являются:
– в первом случае
;
;
;
…………………..
,
а во втором
;
;
…………………..
,
Для
асимптотической устойчивости системы
необходимо и достаточно, чтобы при
все диагональные определители матриц
Гурвица были положительны.
Следствием
критерия Гурвица является условие
нахождения системы на границе устойчивости.
Этим условием является обращение в нуль
последнего (старшего) определителя
Гурвица, т.е.
для первой матрицы и
− для второй. Оно распадается на две
составляющие:
− для первой матрицы
,
что соответствует полюсу, равному нулю,
и
,
что соответствует наличию у
характеристического полинома двух
комплексно-сопряженных корней с нулевой
вещественной частью;
− для второй матрицы
,
что соответствует полюсу, равному нулю,
и
,
что соответствует наличию у
характеристического полинома двух
комплексно-сопряженных корней с нулевой
вещественной частью.
Пример 4.4. Определить условия устойчивости для системы третьего порядка по критерию Гурвица.
Решение. В первой форме записи полином системы представляется следующим образом
. (4.10)
Матрица Гурвица для этого полинома имеет вид
.
Если все коэффициенты полинома положительны, то здесь следует проверить только знак определителя
.
Для того же полинома во второй форме записи
матрица Гурвица имеет вид
.
При положительных коэффициентах полинома для устойчивости системы диагональные определители должны отвечать условиям
;
;
.
Таким образом, помимо положительности всех коэффициентов характеристического полинома условием устойчивости системы является соотношение
▄
Как следует из последнего выражения для устойчивости системы третьего порядка необходимо, чтобы произведение средних коэффициентов характеристического полинома было больше произведения крайних (критерий Вышнеградского).
С помощью критерия Гурвица можно строить границы устойчивости и определять области устойчивости системы в пространстве коэффициентов полиномов (параметров системы управления).
Рассмотрим систему третьего порядка с характеристическим полиномом (4.10). Пусть все его коэффициенты положительны. Проведем замену переменных, не приводящую к изменению расположения корней полинома относительно мнимой оси,
.
Тогда получим другой полином
коэффициенты которого равны
и называются параметрами Вышнеградского. Границе устойчивости в плоскости параметров α и β соответствует гипербола Вышнеградского
α β = 1, приведенная на рис. 4.4. Параметр нормировки Ω называется среднегеометрическим корнем, поскольку
.
Рис. 4.4. Диаграмма Вышнеградского
Для систем высокого порядка определение устойчивости с помощью критерия Гурвица становится трудоемким и избыточным. В этом случае предпочтительнее применение критерия Рауса, позволяющего быстро определить устойчивость системы по коэффициентам характеристического полинома.
Частотные критерии. Частотные характеристики системы управления содержат много информации для определения ее устойчивости. Эти характеристики могут быть получены экспериментально подачей на вход системы синусоидального воздействия и варьирования его частоты.
Как было показано выше, для определения устойчивости замкнутой системы необходимо исследовать ее характеристическое уравнение
,
или в терминах сигнальных графов
. (4.11)
При этом необходимо доказать, что все его корни расположены в левой половине комплексной плоскости. В частотной области эта задача решается отображением графических представлений характеристических полиномов (контуров) на комплексной плоскости.
Отображение
контуров на комплексной плоскости.
Контур – некоторая замкнутая траектория
в плоскости. Поскольку
– комплексная переменная,
,
то любая функция от комплексной переменной
− также комплексная, следовательно, ее
можно представить в виде
и
изобразить на комплексной плоскости в
координатах
и
.
Пример 4.5. Пусть на плоскости p имеем единичный квадрат, показанный на рис 4.5.
Рис. 4.5. Комплексный единичный квадрат
Отобразим
его на
-плоскость
в координатах
и
с помощью функции
.
Решение. Отметим, что отображающая функция имеет один нуль
.
Выразим координаты в плоскости
в координатах в плоскости
:
,
откуда следует
Граничные точки отображения единичного квадрата на -плоскость приведены в табл. 4.1.
Таблица 4.1