Реального интегрирующего звена
Логарифмическая амплитудная частотная характеристика равна
.
Логарифмическая амплитудная частотная и фазовая характеристики реального интегрирующего звена показаны на рис. 3. 71.
Рис. 3.71. Логарифмическая амплитудная частотная и фазовая характеристики
Реального интегрирующего звена
Типовые звенья второго порядка. Типовые звенья второго порядка описываются общим дифференциальным уравнением (3.25). Запишем это дифференциальное уравнение в виде
и представим его в операторной форме
.
Соответствующее ему операторное представление структурной схемы звена приведено на рис. 3.72.
Рис. 3.72. Операторное представление структурной схемы звена второго порядка
Из схемы следует, что звено второго порядка представляет собой последовательность из элементарного усилительного звена и двойного контура с единичным коэффициентом передачи прямого пути и с передаточной функцией обратной связи, равной
.
Передаточная функция этого контура в замкнутом состоянии есть
.
В
зависимости от соотношения между
величинами
и
звено второго порядка ведет себя
по-разному:
– при
в цепи обратной связи ведущую роль
играет контур
и звено ведет себя как апериодическое;
– при
в цепи обратной связи ведущую роль
играет контур
и звено ведет себя как колебательное;
– при
в цепи обратной связи оба контура
равноценны и звено ведет себя как
консервативное.
При
введении параметра
,
который дает возможность представить
передаточную функцию в виде
,
Приведенные выше условия функционирования звена второго порядка могут быть представлены по-другому. Для их определения найдем корни характеристического полинома
Конкретный
вид этих корней зависит от значения
дискриминанта
:
– при
,
т.е. при
,
корни
и
будут вещественными (а при
еще и различными), при этих условиях
рассматриваемое звено называется
апериодическим звеном второго порядка;
– при
,
т.е. при
,
корни
и
представляют собой пару комплексно-сопряженных
корней, и рассматриваемое звено называется
колебательным звеном второго порядка;
– при
,
т.е.
корни
и рассматриваемое звено называется
консервативным звеном второго порядка.
Рассмотрим указанные звенья подробнее.
Апериодическое
звено второго порядка.
При
корни характеристического полинома
действительны и равны
.
Это позволяет разложить характеристический полином на множители
и представить передаточную функцию в виде
,
при этом условие апериодичности преобразуется к виду: T3 > T4. Из выражения передаточной функции видно, что апериодическое звено второго порядка эквивалентно последовательному включению двух апериодических звеньев первого порядка с общим коэффициентом передачи k и постоянными времени T3 и T4.
Операторное представление переходной функции апериодического звена второго порядка имеет вид
,
а ее оригинал есть
.
Графическое изображение переходной функции приведено на рис. 3.73.
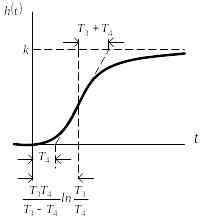
Рис. 3.73. Переходная функция апериодического звена второго порядка
Импульсная переходная функция апериодического звена второго порядка имеет вид
.
Вид этой функции показан на рис. 3.74.
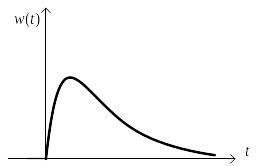
Рис. 3.74. Весовая функция апериодического звена второго порядка
Частотная передаточная функция апериодического звена второго порядка определяется выражением
,
а ее графическое представление имеет вид, приведенный на рис. 3.75.
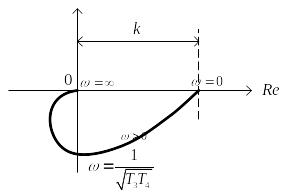
Рис. 3.75. Годограф апериодического звена второго порядка
Из последнего выражения умножением на комплексно-сопряженное
знаменателю число получаем вещественную
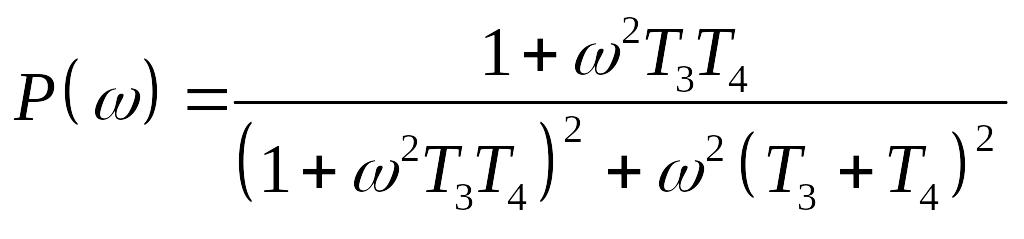
и мнимую
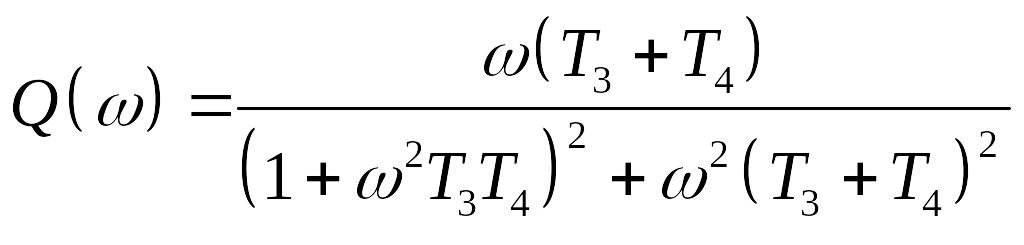
частотные характеристики.
Амплитудная характеристика апериодического звена второго порядка имеет вид
и приведена на рис. 3.76 (для положительных частот).
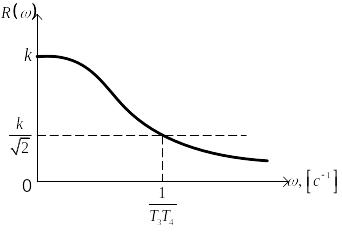
Рис. 3.76. Амплитудно-частотная характеристика
апериодического звена второго порядка
Выражение фазовой характеристики апериодического звена второго
порядка имеет вид
.
Логарифмическая амплитудная частотная характеристика апериодического звена второго порядка определяется выражением
Построение
асимптотической логарифмической
амплитудной частотной характеристики
производится следующим образом. Левее
первой сопрягающей частоты, т.е. при
и представляет собой горизонтальную
линию (линию с нулевым наклоном). При
и представляет собой прямую с наклоном,
равным –20 дБ/дек. Наконец, для
и представляет собой прямую с наклоном,
равным – 40 дБ/дек.
Графическое представление логарифмических характеристик апериодического звена второго порядка показано на рис. 3.77.
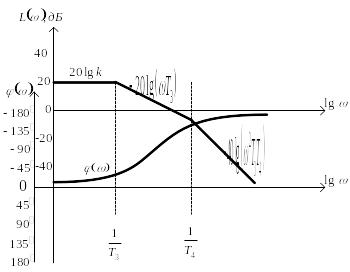
Рис. 3.77. Графическое представление логарифмических характеристик
апериодического звена второго порядка
Примером апериодического звена второго порядка может служить RLC-цепь, приведенная на рис. 2.6.
Сравнивая описывающее его дифференциальное уравнение (2.5)
или
с общим дифференциальным уравнением (3.25)
или в операторной форме
,
получаем, что они эквивалентны при
,
или
,
при
этом корни характеристического уравнения
равны
.
Условие
апериодичности
трансформируется в соотношение
или
.
Колебательное
звено
отличается тем, что для него постоянные
времени (инерционности)
T1
и T2
связаны соотношением
.
Это значит, что детерминант
и, следовательно, корни характеристического
уравнения являются комплексными
,
где
– круговая частота,
– собственная частота колебательного
звена,
– коэффициент затухания.
Передаточная характеристика звена может быть представлена в общем виде как
Операторное изображение переходной функции есть
.
Оригинал переходной функции
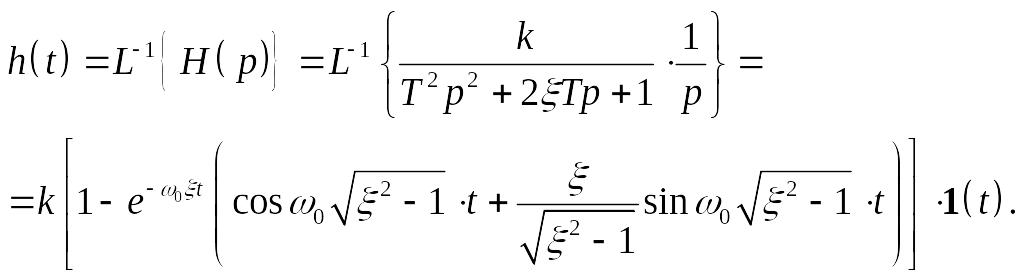
Вид переходной функции иллюстрируется рис.3.78.
Импульсная переходная (весовая) функция есть производная переходной функции.
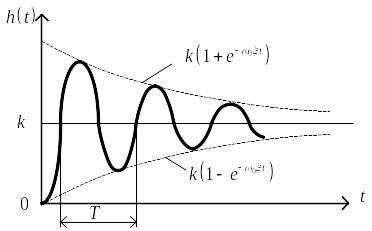
Рис. 3.78. Переходная функция колебательного звена
Вид импульсной переходной функции показан на рис. 3.79.
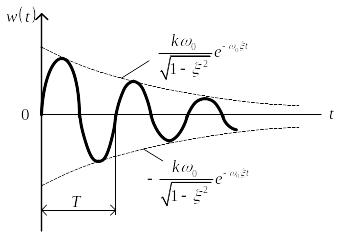
Рис. 3.79. Импульсная переходная функция колебательного звена
Частотная передаточная функция колебательного звена имеет вид
.
График частотной характеристики в обычном масштабе при
различных
значениях
имеет вид, показанный на рис. 3.80.
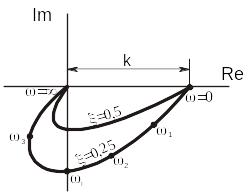
Рис. 3.80. Частотная характеристика колебательного звена
Действительная частотная характеристика есть
,
а мнимая частотная характеристика есть
.
Амплитудная частотная характеристика имеет вид
,
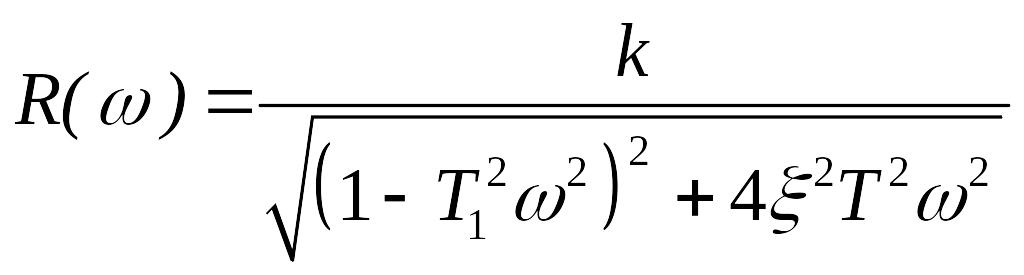а фазовая частотная
.
Логарифмическая амплитудная характеристика
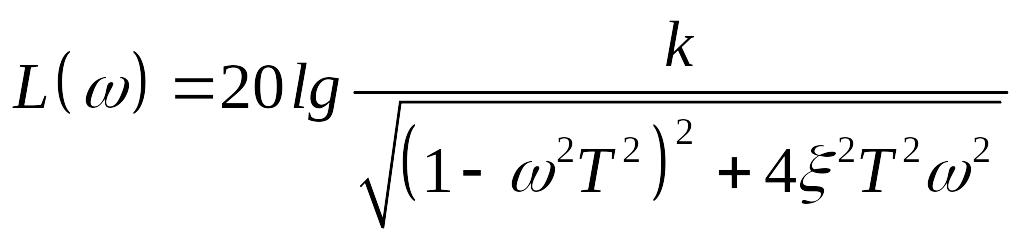
или
.
Построение
асимптотической логарифмической
амплитудной характеристики производится
на основе следующих соображений. Пусть
,
тогда
.
На низких частотах
,
тогда
.
На высоких частотах
,
тогда
.
В области средних частот
или
.
На
рис. 3.81 приведена логарифмическая
амплитудная характеристика колебательного
звена при различных значениях
.
Асимптотическая
логарифмическая амплитудная характеристика
представляет собой ломаную линию,
состоящую из двух асимптот, к которым
стремится логарифмическая амплитудная
характеристика при
и при
.
Первая асимптота – ось абсцисс при
.
В общем же случае она идет вдоль оси
абсцисс на расстоянии
.
Вторая асимптота имеет наклон –40 дБ/дек.
Точка пересечения асимптот соответствует
частоте
.
Если
,
то расхождение между асимптотической
и истинными логарифмическими амплитудными
характеристиками не
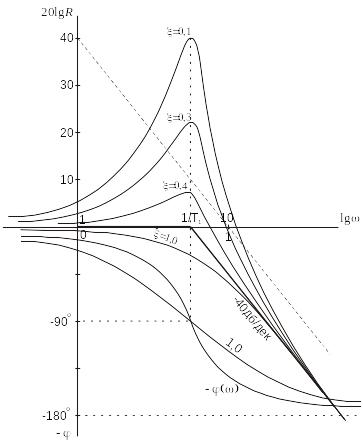
Рис. 3.81. Логарифмическая амплитудная характеристика
колебательного звена
превышает 3дБ, поэтому для таких звеньев можно пользоваться асимптотическими логарифмическими амплитудными характеристиками.
Вблизи
точки резонанса (т.е. при
)
асимптотическую логарифмическую
амплитудную характеристику корректируют
с помощью графиков поправок, приведенных
в литературе, например, в [2] (рис.3.83).
Поправка
(т.е. разница между действительной
и асимптотической
частотными характеристиками) зависит
от степени затухания
Фазовая частотная характеристика равна
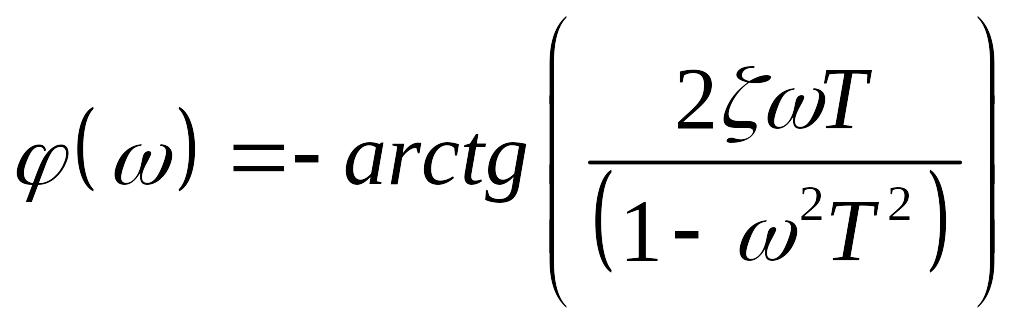
и
при
,
.
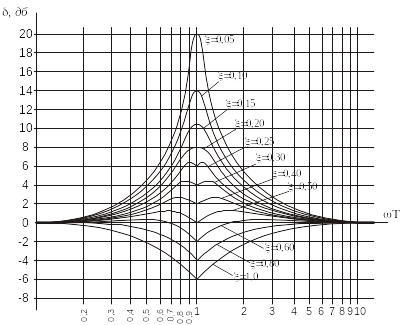
Рис. 3.83. График поправок для коррекции ЛАХ
Пример 3.4. Показать, что двигатель постоянного тока (рис. 3.82) является колебательным звеном.
Решение. Он описывается следующими уравнениями:
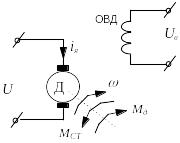
Рис. 3.82. Электрическая схема двигателя постоянного тока
;
;
;
,
где
–
входное напряжение якоря двигателя
(входной сигнал);
–
скорость
вращения двигателя (выходной сигнал);
–
постоянные
коэффициенты;
–
момент
инерции якоря двигателя;
– момент,
развиваемый двигателем и момент
сопротивления.
Положим
.
Решив совместно приведенные уравнения
относительно
и
,
получим
и
.
Разделим
левую и правую часть на
,
где
– коэффициент передачи двигателя (1/с).
Обозначив
и
,
получим
.
▄
Примером колебательного звена может также служить RLC-цепь, приведенная на рис. 3.83 при .
Консервативное звено представляет собой идеальное звено, в котором пренебрегается влиянием рассеяния энергии. Оно является частным случаем звена второго порядка при ζ = 0. В этом случае
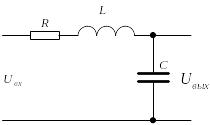
Рис. 3.83. Пример реализации колебательного звена
передаточная функция консервативного звена имеет вид:
,
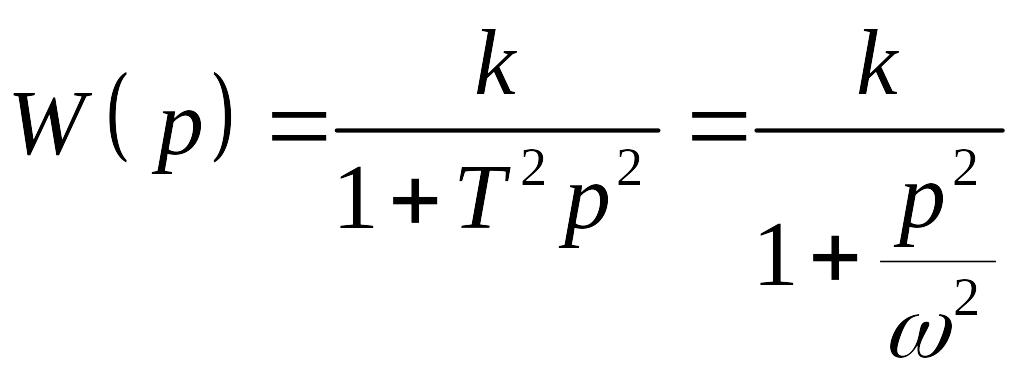где
ω
– угловая
частота,
.
Переходная функция звена есть
,
а весовая функция
.
Логарифмическая амплитудная характеристика определяется выражением
,
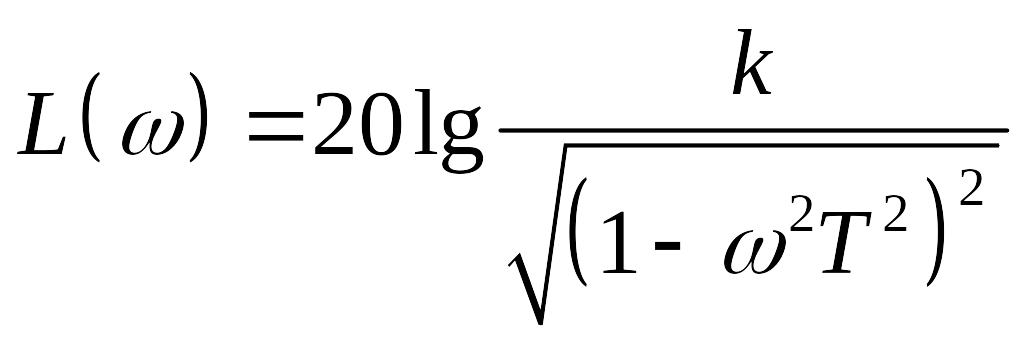а фазовая частотная характеристика – выражением
.
Графики этих характеристик читателю предлагается построить самостоятельно.