Форсирующего звена

Реальное дифференцирующее звено (инерциальное, дифференциальное звено с замедлением) в отличие от идеального реализуется только при наличии помех, т.е. обладает конечной инерционностью.

Дифференциальное уравнение звена имеет вид

.

Представим записанное уравнение в виде

,

или в операторной форме

. (3.36)

Последнему выражению соответствует операторная структурная схема реального дифференцирующего звена, показанная на рис. 3.60.

Рис. 3.60. Операторная структурная схема

Реального дифференцирующего звена

Воспользовавшись правилами эквивалентных преобразований структурных схем, перенесем точку приложения сигнала обратной связи вправо, на вход усилительного звена, тогда операторная структурная схема приобретает вид, показанный на рис. 3.61.

Нетрудно видеть, что этому преобразованию соответствует вынесение общего множителя p в выражении (3.36). Теперь реальное дифференцирующее звено может быть рассмотрено как последовательное соединение элементарного дифференцирующего звена с передаточной

Рис. 3.61. Преобразованная операторная структурная схема

Реального дифференцирующего звена

функцией

и встречно-параллельного соединения усилительного звена и звена чистого запаздывания с передаточной функцией

.

Операторное изображение переходной функции есть

.

Оригинал переходной функции есть обратное преобразование Лапласа ее операторного представления

.

Она изображена на рис. 3.62.

Рис. 3.62. Переходная функция реального дифференцирующего звена

Импульсная переходная (весовая) функция есть

.

Она имеет вид, показанный на рис. 3.63.

Рис.3.63. Импульсная переходная функция

Реального дифференцирующего звена

Частотная передаточная функция определяется как

.

Амплитудная частотная характеристика есть

,

она приведена на рис. 3.64.

Рис. 3.64. Амплитудная частотная характеристика

Реального дифференцирующего звена

Фазовая частотная характеристика есть

.

Логарифмическая амплитудная характеристика определяется как

и при k = 1 имеет вид, показанный на рис. 3.65.

При амплитудная характеристика перемешается параллельно самой себе по вертикали на величину k.

Примером реального дифференцирующего звена является простей-

Рис. 3.65. Логарифмическая амплитудная и фазовая частотные характеристики

Реального дифференцирующего звена

шая RC-цепь, приведенная на рис. 3.66.

Рис. 3.66. Пример реального дифференцирующего звена

Для этой цепи имеем

или

.

Переходя к изображениям и решая последнее уравнение относительно тока, получим

,

.

Реальное интегрирующее звено (интегрирующее звено с замедлением, инерциальное интегрирующее звено) описывается дифференциальным уравнением

.

Представим записанное уравнение в виде

или в операторной форме

.

Последнему выражению соответствует операторная структурная схема реального интегрирующего звена, показанная на рис. 3.67.

Рис. 3.67. Операторная структурная схема реального интегрирующего звена

Непосредственно из рис. 3.67 следует, что реальное интегрирующее звено можно представить последовательностью:

– последовательной цепочки интегратора и усилителя с коэффициентом усиления k с передаточной функцией

;

– контура, состоящего из дифференциатора и элемента запаздывания с передаточной функцией

.

В результате последовательного соединения перечисленных компонентов получим передаточную функцию реального интегрирующего звена в виде

.

Для нахождения временных характеристик представим передаточную функцию в виде

.

Это позволяет представить реальное интегрирующее звено последовательностью интегрирующего и апериодического звеньев.

Операторное изображение переходной функции выглядит как

,

а ее оригинал имеет вид

.

Графическое представление переходной функции реального интегрирующего звена приведено на рис. 3.68.

Рис. 3.68. Переходная функция реального интегрирующего звена

Весовая функция определяется как

,

а ее графическое представление приведено на рис. 3.69.

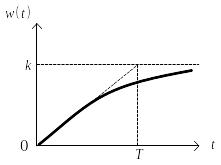
Рис. 3.69. Весовая функция реального интегрирующего звена

Частотная передаточная функция звена есть

.

Представим ее в виде суммы действительной и мнимой частей

,

и получим амплитудную частотную характеристику в виде

.

Ее графическое представление показано на рис. 3.70.

Фазовая частотная характеристика реального интегрирующего звена определяется как

.

Рис. 3.70. Амплитудная частотная характеристика