3. Структурные методы теории автоматического управления

3.1. Понятие структуризации

Математическое описание системы автоматического управления начинается с разбиения её на типовые по математическому описанию звенья. По уравнениям или характеристикам отдельных звеньев составляются уравнения или характеристики системы в целом. Разбиение на типовые звенья по математическому описанию позволяет перейти от необозримого множества физических элементов к конечному числу звеньев.

Структурная схема системы автоматического управления составляется из типовых звеньев направленного действия. Звеном направленного действия называется звено, которое передает воздействие только в одном направлении со входа на выход. Пример операторного представления структурной схемы системы управления показан на рис. 3.1.

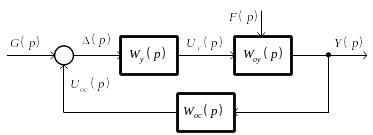
Рис. 3.1. Операторное представление структурной схемы системы

Получение структурной схемы в большинстве случаев является конечной целью математического описания системы. Для получения такого описания необходимо:

– знать правила преобразования структур, образованных из звеньев с заданными передаточными функциями;

– иметь математические описания типовых звеньев, из которых строятся структурные схемы произвольных систем.

Рассмотрим перечисленные компоненты математического описания структурных схем систем управления в предложенной последовательности.

Лекция 9

3.2. Преобразования структурных схем

Преобразование структурных схем в моделях «вход-выход». Структурные схемы для реальных систем автоматического управления часто имеют сложный и запутанный вид. С целью упрощения структурной схемы или приведения ее к более удобному виду, можно производить структурные преобразования по определенным правилам. Для моделей «вход-выход» эти правила суть правила определения структур передаточных функций последовательного, параллельного соединения звеньев, а также соединения звеньев с обратной связью путем получения передаточной функции эквивалентного звена. Рассмотрим их, используя представление звеньев в форме дифференциальных уравнений

, (3.1)

передаточных функций

, (3.2)

временных

(3.3)

и частотных

(3.4)

характеристик.

Последовательное соединение. Дифференциальные уравнения системы, образованной последовательным соединением звеньев (рис. 3.1)

Рис. 3.1. Последовательное соединение звеньев

запишутся в виде

(3.5)

(3.6)

. (3.7)

Исключая переменные и в уравнениях (3.5) и (3.6), получим операторные полиномы уравнения (3.2)

.

Тогда передаточная функция последовательного соединения получается в виде

. (3.8)

Временнáя характеристика (импульсная переходная функция) последовательного соединения звеньев получается обратным преобразованием Лапласа передаточной функции

.

Амплитудная частотная характеристика последовательного соединения звеньев равна произведению

,

а фазовая частотная – сумме

соответствующих звеньев.

Логарифмическая частотная характеристика последовательного соединения есть сумма

.

Пример графического построения асимптотической ЛАЧХ последовательного соединения интегрирующего звена и апериодического звена второго порядка приведен на рис. 3.3.

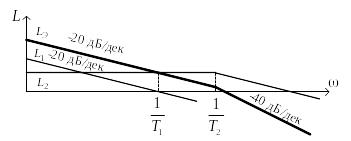
Рис. 3.3. Построение ЛАЧХ последовательного соединения звеньев

Если передаточная функция имеет простой диполь, т.е. общий для полиномов числителя и знаменателя корень

,

то соответствующий коэффициент разложения на сумму простейших дробей

равен нулю.

Это значит, что реакция последовательного соединения на единичную δ-функцию при нулевых начальных условиях будет неполной (не содержит слагаемого, соответствующего полюсу p_i). Такая ситуация может иметь место, если эти диполи имеют передаточные функции звеньев или , а также если

или

,

т.е. если нуль одного звена компенсирует полюс другого. В этом случае

передаточные функции, а, следовательно, частотные и временные характеристики соединения не полностью отражают свойства системы.

Параллельное соединение. Дифференциальные уравнения парал-

лельного соединения звеньев (рис. 3.4)

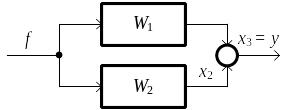
Рис. 3.4. Параллельное соединение звеньев

запишутся в виде

; (3.9)

; (3.10)

; (3.11)

.

Исключая из (3.9) – (3.11) переменные и , получим операторные полиномы выражения (3.1)

.

Тогда передаточная функция параллельного соединения получается в виде

. (3.12)

Временнáя характеристика (импульсная переходная функция) является суммой временных характеристик звеньев

.

Вещественная и мнимая частотные характеристики параллельного соединения звеньев получаются суммированием соответствующих характеристик звеньев

;

,

а амплитудная частотная характеристика вычисляется обычным образом:

.

Фазовая частотная характеристика вычисляется по амплитудно-частотной характеристике

.

Логарифмическая частотная характеристика параллельного соединения определяется на основе амплитудной частотной характеристики обычным порядком:

.

Передаточная функция параллельного соединения имеет диполь, если:

– диполь имеет одна из передаточных функций;

– звенья имеют одинаковые полюсы

.

Соединение с обратной связью (встречно-параллельное соединение). Дифференциальные уравнения такого соединения (рис. 3.5.)

Рис. 3.5. Соединение звеньев с обратной связью

запишутся в виде

; (3.13)

; (3.14)

; (3.15)

,

где знак «минус» соответствует отрицательной обратной связи, а «плюс» – положительной.

Исключая в (3.13) – (3.15) переменные , и , получим операторные полиномы уравнения (3.1)

.

Тогда передаточная функция (3.2) соединения с обратной связью получается в виде

. (3.16)

В последних двух формулах знак «минус» соответствует положительной обратной связи, а «плюс» – отрицательной.

Временнáя (импульсная переходная) функция сложным образом зависит от временных характеристик звеньев, поэтому удобнее получать ее обратным преобразованием Лапласа эквивалентной передаточной функции

Комплексная частотная характеристика соединения с обратной связью

(3.17)

также сложно зависит от частотных характеристик звеньев.

Свойства системы с обратной связью определяются усилением разомкнутого контура с передаточной функцией

на различных частотах. Если усиление контура мало, то обратной связью можно пренебречь, поскольку на частотах, где

можно принять

.

Практически усиление контура при

считается малым.

Аналогично на частотах, где выполняется условие

можно принять

,

т.е. частотная характеристика соединения с обратной связью близка к частотной характеристике обратной связи. Усиление контура считается большим, если

.

На остальных частотах, где , т.е. там, где

необходимо пользоваться точной формулой (3.17).

Пример 3.1. Получить эквивалентную передаточную функцию системы, образованной встречно-параллельным соединением звеньев с передаточными функциями и , представленной на рис. рис.3.6, а, с логарифмическими амплитудно-частотными характеристиками соединения, представленными на рис. 3.6, б (сплошные линии).

а б

Рис. 3.6. Пример реализации соединения звеньев с обратной связью:

а - операторная структурная схема; б – логарифмическая амплитудно-частотная характеристика соединения

Решение. Эквивалентная передаточная функция системы определяется как

,

где

.

Подставляя значение передаточной функции разомкнутой системы в выражение для эквивалентной передаточной функции, получим

.

Импульсная переходная функция

Комплексная частотная характеристика

.

На частотах с^–1 усиление контура превышает 20 дБ, следовательно, амплитудно-частотная характеристика на этих частотах определяется только свойствами звена обратной связи. В то же время на частотах с^–1 усиление контура меньше 20 дБ, т.е. контур как бы разомкнут, и свойства системы определяются только свойствами звена прямой передачи. Логарифмическая амплитудная частотная характеристика эквивалентной замкнутой системы изображена на рис.3.6, б пунктирной линией.

■

Передаточная функция системы с обратной связью неполна, т.е. имеет диполь, если диполь имеет передаточная функция одного из звеньев или если нуль звена в прямом пути равен полюсу звена обратной связи. Последнее означает, что наибольший общий делитель

нетривиален. При этом никакими воздействиями при нулевых начальных условиях нельзя полностью обнаружить собственные свойства замкнутой системы.

Диполь системы с обратной связью также означает наличие диполя у передаточной функции разомкнутого контура . На комплексной частоте нуля передаточной функции усиление такого контура равно нулю (контур как бы разомкнут).

Преобразования структурных схем в моделях с раскрытой структурой. Раскрытыми моделями объектов и систем управления являются модели в виде графов, структурных схем или дифференциальных уравнений в причинно-следственной форме. Задачей рассмотрения таких моделей является преобразование их в модели «вход-выход», т.е. построение передаточных функций, частотных или временных характеристик. Для определения передаточной функции системы необходимо выполнить одно из следующих действий:

1. Записать систему уравнений, описывающих используемую модель

и воспользоваться, например, правилом Крамера

,

где полиномиальная матрица в матричном представлении системы уравнений получается из матрицы заменой q-го столбца r-м столбцом матрицы . Знаменатель передаточной функции независимо от номеров входа r и выхода q один и тот же – характеристический полином системы:

.

2. Выполнить эквивалентные преобразования исходной системы одним из следующих способов:

– последовательным сворачиванием графа системы по правилам эквивалентных преобразований;

– применением формулы Мейсона.

Применение формулы Мейсона выше уже рассмотрено достаточно подробно, поэтому рассмотрим только правила эквивалентных преобразований графов.

Правила эквивалентного преобразования графов соответствуют правилам исключения внутренних переменных в системах уравнений.

Пример 3.2. Пусть система задана структурной схемой, представленной на рис. 3.8 с входной переменной и выходной переменной .

Рис. 3.8. Структурная схема системы

Процесс получения эквивалентной передаточной функции состоит в последовательном «свертывании» структурной схемы. Процесс свертывания может быть неоднозначным. Можно, например, провести его в следующем порядке. Звенья и образуют контур, который можно заменить одним звеном с передаточной функцией

.

Теперь в прямом пути все звенья соединены последовательно, следовательно, их можно заменить одним звеном с передаточной функцией

.

Замыкая выход с входом, получим типовую структуру с положительной обратной связью с передаточной функцией

.

▄

Последовательность преобразований, использующих только три рассмотренные выше правила преобразований для типовых структур, возможна не всегда. Для этого граф должен иметь только типовые подграфы, т.е. подграфы, представляющие собой последовательное, параллельное, либо встречно-параллельное соединение вершин. На рис. 3.9 приведен фрагмент графа, не имеющий типовых подграфов.

Рис. 3.9. Граф, не имеющий типовых подграфов

Для его преобразования необходимо ввести дополнительные правила – правила переноса вершин съема и суммирования сигналов. Эти правила иллюстрируются рис. 3.10 и 3.11 соответственно.

Рис. 3.10. Иллюстрация правила переноса вершины съема

Рис. 3.11. Иллюстрация правила переноса вершины суммирования

Пример 3.3. Получить эквивалентную передаточную функцию графа с нетиповыми подграфами, приведенного на рис. 3.9, с использованием

правил переноса вершин съема и суммирования сигналов.

Решение. Изобразим структуру графа в более понятном виде, показанном на рис. 3.12.

Используя правила переноса вершин съема и суммирования сигналов, перенесем вершины съема в графе на рис 3.12. Для этого вместо дуги (3,1) введем дугу (3,2) с передаточной функцией , а вместо дуги (4,1) введем дугу (4,2) с передаточной функцией . В результате получим

Рис 3.12. Граф, не имеющий типовых подграфов

граф, показанный на рис. 3.13.

Рис. 3.13. Преобразованный фрагмент графа, изображенного на рис. 3.9

Он состоит из последовательного соединения звена W₁ и части, включающей звенья W₂ ÷ W₄ с обратными связями. Прямой путь этой части имеет передаточную функцию

,

а передаточная функция цепи обратной связи есть

.

Тогда передаточная функция системы имеет вид

■

Замечания.

– структурные преобразования можно производить только в том случае, если анализ динамической системы производится при нулевых начальных условиях, в противном случае структурные преобразования приводят к потере начальных условий и погрешностям при дальнейшем анализе;

– преобразуемая система не должна иметь диполей;

– структурные преобразования лишены физического смысла.