2.4.3. Модели с раскрытой структурой

Общие сведения. Структура системы – совокупность элементов и причинно-следственные связи направленного действия между ними. Понятия системы и структуры близки по смыслу, хотя и вложены друг в друга: мы говорим о структуре системы, а не наоборот. Отношения этих понятий эквивалентны отношениям на множествах, а наиболее понятным средством представления этих отношений являются графы – универсальный аппарат описания структур систем.

Граф – это система некоторых объектов вместе с парами этих объектов, отображающая отношение между ними. Графами удобно изображать различные диаграммы, системы отношений, структурные химические формулы и т. п.

Более строго, графом G называется система (V, U, ф), где V={v}– множество вершин, U={u} – множество ребер, ф – функция инциденции, ставящая в соответствие каждому ребру упорядоченную вершину (или упорядоченную пару вершин , называемых концами ребра).

При небольшом числе элементов и связей используются диаграммы графов, т.е. их геометрические образы. Они представляют топологию системы. Топология позволяет выявить существенные свойства систем даже без раскрытия свойств вершин и дуг, которые обнаруживаются при дальнейшем раскрытии свойств системы за счет уточнения структур операторов-вершин и связей-дуг. Существует довольно большое число типов графов: ориентированные, плоские и т.д.

В зависимости от подхода к моделированию систем и конкретного содержания элементов множества (набора элементов модели) и отношений (связей между элементами) модели с раскрытой структурой представляются структурными схемами, сигнальными графами, системами дифференциальных уравнений в причинно-следственной форме и некоторыми другими средствами.

Структурные графы. Структурная схема – графическое отображение причинно-следственной связи звеньев. В односвязных системах любое звено может иметь некоторое число входов (рис. 2.23, а), оно преобразует их функциональную сумму в единственную переменную выхода в соответствии с некоторым оператором (рис. 2.23, б). В многосвязной системе выходные переменные составляют некоторое множество.

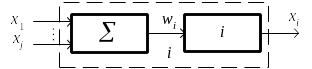
а б

Рис. 2.23. Представление звена системы: а – структурное, б – функциональное

В частном случае оператора тождественного преобразования звено выступает как сумматор.

С точки зрения теории графов структурная схема является ориентированным графом , определяемым парой множеств: множеством вершин и множеством дуг , связывающих пары вершин. Вершины соответствуют звеньям, а дуги – связям. Вершина – это звено общего вида, суммирующее переменные всех входящих дуг. Дуга – компонент, задающий причинно-следственную связь между звеньями. В итоге структурная схема представляется структурным графом (С-графом), в котором отсутствуют звенья суммирования (рис. 2.24).

Теоретико-множественное описание систем дает естественный способ ввода и редактирования систем управления как последовательного раскрытия их по рангам неопределенности. Моделью нулевого структурного ранга системы M_s(0) является все множество звеньев. Для графа,

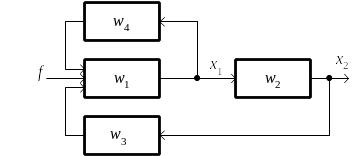
Рис 2.24. Структурный граф системы

приведенного на рис. 2.24, это множество перечисляется так:

W = {w₁, w₂, w₃, w₄}.

При однотипных звеньях можно ограничиться заданием мощности множества: │W│ = 4.

Дополнение модели M_s(0) множеством связей

X = {(1,3), (1,4), (2,1), (3,2), (4,1)},

где цифры означают номера звеньев, дает модель M_s(1) первого структурного ранга, т.е. модель топологии системы.

Дальнейшее раскрытие неопределенности состоит в задании операторов вершин, т.е. передаточных функций звеньев, определяемых отношениями полиномов

.

Задание их структур сводится к указанию степеней n_i и m_i полиномов A_i и B_i, в результате образуется модель системы M_s(2) второго, т.е. структурного ранга. Если для рассматриваемого примера передаточные функции звеньев есть

, , , ,

то информацию о структурах операторов можно закодировать массивами степеней полиномов числителей и знаменателей передаточных функций: {0,0,0,1} и {0,2,0,1}.

Результат конкретизации значений всех коэффициентов полиномов – полностью определенная модель M_s(3) третьего, параметрического, ранга. В результате получаем описание автономной системы (т.е. собственно системы, вне связи со средой).

Для описания связей системы со средой необходимо указать звено, на которое подается входное воздействие, а также звено, выход которого является выходом системы.