2.4.2. Модели «вход-выход»

Способы построения моделей «вход-выход». Как было показано выше, основными формами представления операторов преобразования входных переменных f(t) в переменные выхода y(t) в функциональном пространстве являются дифференциальные уравнения, передаточные функции, временные и частотные характеристики. Эти представления могут быть приняты за основу задания динамических свойств в терминах «вход-выход». Рассмотрим применение их для построения моделей линейных систем управления.

Построение моделей «вход-выход» по системе дифференциальных уравнений. Пусть задана система дифференциальных уравнений

;

.

Построение модели в терминах «вход-выход» означает исключение внутренних переменных и получение прямой зависимости выхода от входа. Это проще сделать, если перейти к алгебраической форме уравнений, приняв начальные условия нулевыми:

; (2.33)

.

Построение модели по этой системе уравнений можно выполнить различными способами. Рассмотрим некоторые из них.

Последовательное исключение переменных применяется при небольшом числе уравнений системы (2.33). Пусть имеем объект с одним входом f, одним выходом y и двумя внутренними переменными x₁ и x₂. Описывающая его система уравнений имеет вид

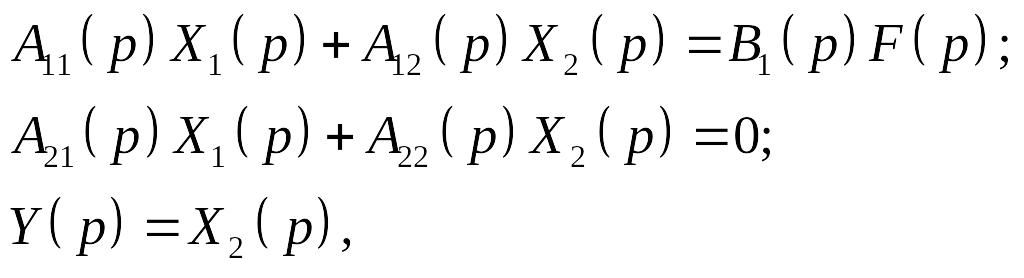(2.34)

где A_ij – компоненты матрицы А.

Опуская оператор отображения p, из второго уравнения (2.34) получаем

.

Подставим полученное выражение в первое уравнение (2.34) и определим выражение для выхода

.

Отсюда выражение для передаточной функции есть

. (2.35)

По выражению (2.35) уже легко получить полиномы числителя и знаменателя передаточной функции и записать выражение для одного дифференциального уравнения.

Пример 2.19. Запишем, например, предыдущую систему дифференциальных уравнений в матричной форме

; .

Определяем характеристический полином

;

Числитель передаточной функции определяется как детерминант матрицы при замене ее второго столбца столбцом свободных членов

.

Тогда выражение для передаточной функции получается снова в виде (2.35).

▄

Матричный способ применяется при построении моделей многомерных систем. Пусть имеем систему алгебраических уравнений:

,

.

Передаточная матрица системы в общем случае выражается как

. (2.36)

При этом полиномиальная матрица системы A должна быть неособенной (т.е. ее определитель не равен тождественно нулю). Поскольку

, (2.37)

где – присоединенная матрица, то выражение для передаточной функции приобретает вид

.

Пример 2.19. Характеристический полином A(p) для системы из предыдущего примера уже вычислен. Присоединенная матрица для матрицы A выглядит так:

.

Числитель передаточной функции вычислим, используя (2.36)

.

Для одномерной системы (k = r = 1) полиномиальную матрицу числителя передаточной матрицы можно также вычислять как определитель блочной матрицы

. (2.38)

Определитель блочной матрицы (2.38) для нашего примера равен

,

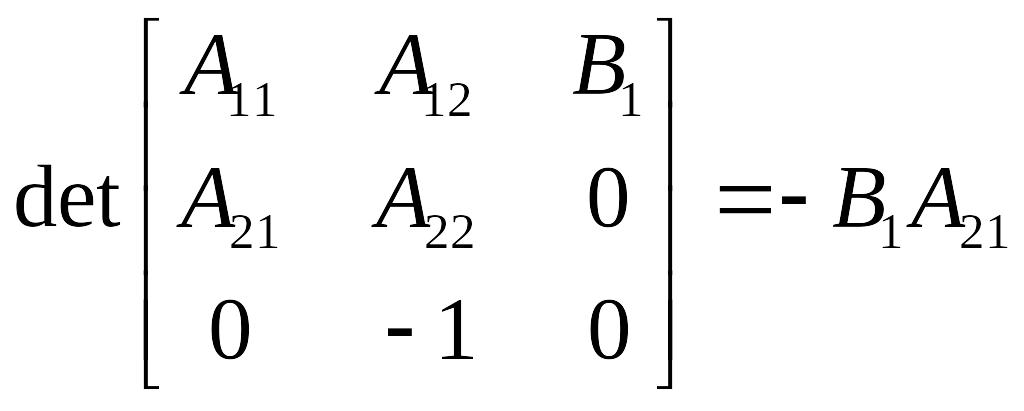т.е. имеет значение, совпадающее со значением из предыдущего примера.

■