2.4. Линейные модели систем управления
2.4.1. Понятие линеаризации моделей
Виды линеаризации. Выше было отмечено, что большинство физических реализаций систем управления являются нелинейными. Однако для относительно небольших изменений переменных (например, вблизи рабочей точки системы) такие системы можно рассматривать как линейные. Применимость линейного представления для конкретной системы решается с учетом ее природы. Так механические и электрические системы линейны в достаточно широком диапазоне изменения переменных, а тепловые и гидравлические системы нелинейны в принципе.
Линеаризацию систем можно проводить:
– в
окрестности рабочей точки системы
(метод
касательных);
– на
интервале
(метод хорд);
– путем линеаризации дифференциальных уравнений, описывающих систему.
При линеаризации нелинейной функции по методу касательных зада-
ча решается, например, разложением нелинейной функции в ряд Тейлора в окрестности рабочей точки.
Пусть связь между входом системы описывается уравнением
.
Непрерывную функцию в рабочей точке (рис. 2.20) можно разложить в ряд Тейлора
.
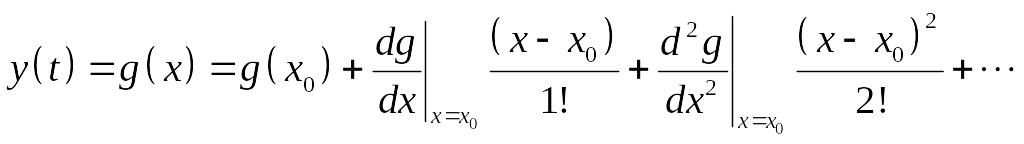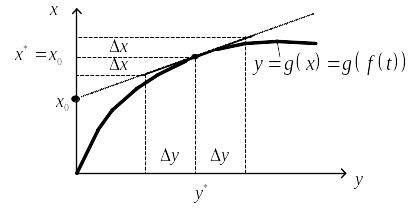
Рис. 2.20. Линеаризация функции в окрестности рабочей точки
Для получения линейной аппроксимации зависимости выхода от входа достаточно ограничиться первыми двумя членами этого разложения
,
где
m
– тангенс угла наклона касательной к
кривой
в рабочей точке
.
Из последнего выражения получаем
или
.
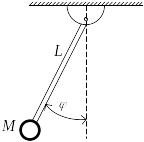
Пример 2.18. Рассмотрим решение задачи линеаризации для системы, представляющей собой свободно колеблющийся маятник, показанный на рис. 2.21, а.
а б
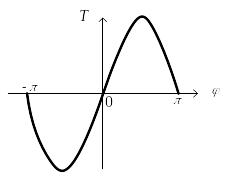
Рис. 2.21. Свободно колеблющийся маятник: a – структурная схема;
б – зависимость момента от угла поворота
При отклонении маятника от вертикального положения на массу M действует момент силы
,
где g – ускорение силы тяжести.
Условию равновесия соответствует φ = 0. Зависимость между T и φ является нелинейной и имеет вид, показанный на рис. 2.21, б.
Вычислим первую производную в точке равновесия и получим линейную аппроксимацию последнего уравнения.
,
где
.
Следовательно
.
Полученная
аппроксимация приемлема в диапазоне
.
Так, при колебании системы в пределах
от положения равновесия колебания
линейной модели отличаются от
действительных колебаний маятника
всего на 2%!
▄
При линеаризации нелинейной функции на интервале (рис. 2.22)
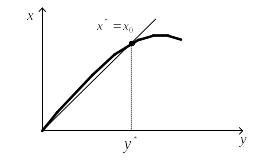
Рис. 2.22. Линеаризация функции на интервале 0 ÷
линейная аппроксимация имеет вид
,
где
.
Пусть
нелинейная функция задана (известна) в
виде математического (аналитического)
описания, например
,
где x1
и x2
– входные координаты и y
допускает хотя бы одно дифференцирование
по обеим координатам. Раскладываем эту
функцию в ряд Тейлора в окрестности
точки установившегося режима
и
при малых отклонениях
и
.
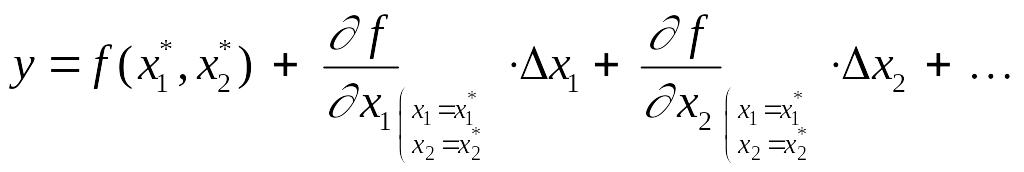
Последнее уравнение представляет собой члены 1-го порядка ряда Тейлора нелинейной функции . Таким образом, исходную нелинейную зависимость двух переменных мы заменили линейной комбинацией отклонений от установившегося режима.
При
зависимости y
от нескольких переменных
разложение в ряд Тейлора в рабочей
точке
с координатами
выглядит
как
.
Теперь рассмотрим линеаризацию дифференциальных уравнений. Пусть нелинейное дифференциальное уравнение, описывающее поведение нелинейного динамического объекта, имеет вид
.
(2.30)
При
линеаризации, как и ранее, в качестве
рабочей точки выбирается точка
установившегося режима или точка
равновесного состояния. Под установившемся
состоянием понимается такой режим
работы, когда
,
т.е. в объекте не происходит никаких
изменений:
,
где
– соответственно, значения векторов
состояния и управления в установившемся
режиме (статике).
Далее,
правую часть (2.30) раскладываем в ряд
Тейлора в точке
при малых изменениях
:
, (2.31)
где
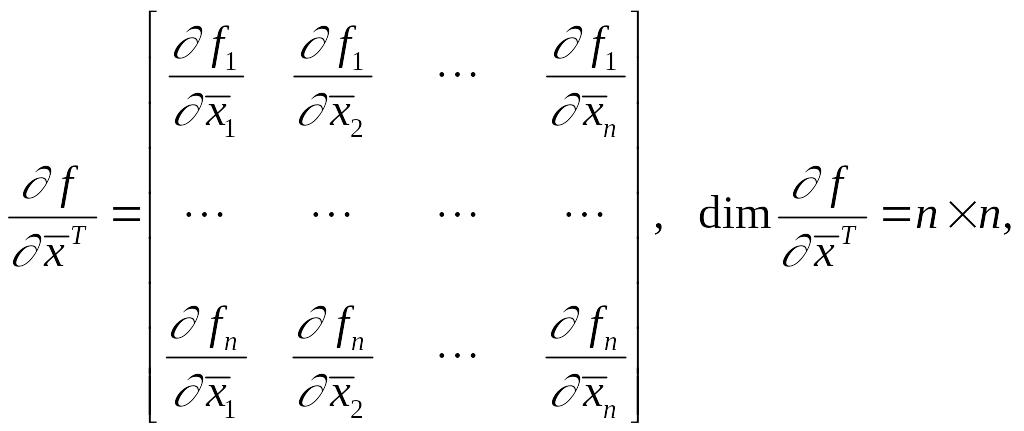
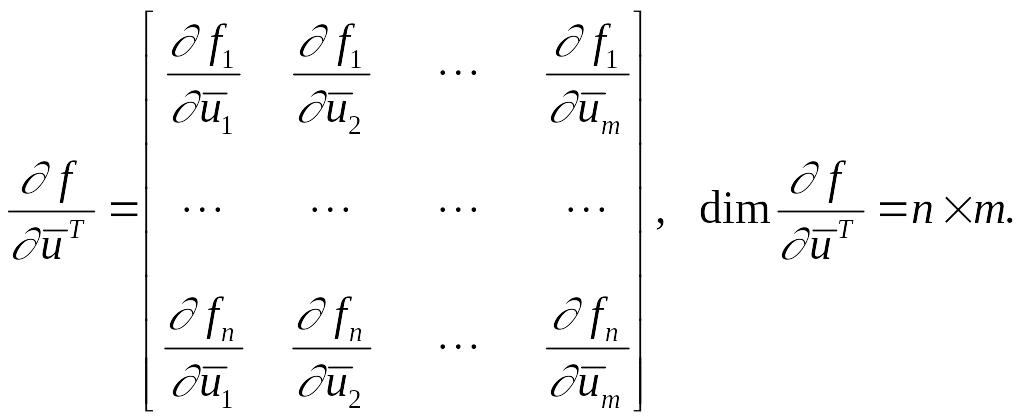
Обозначим
;
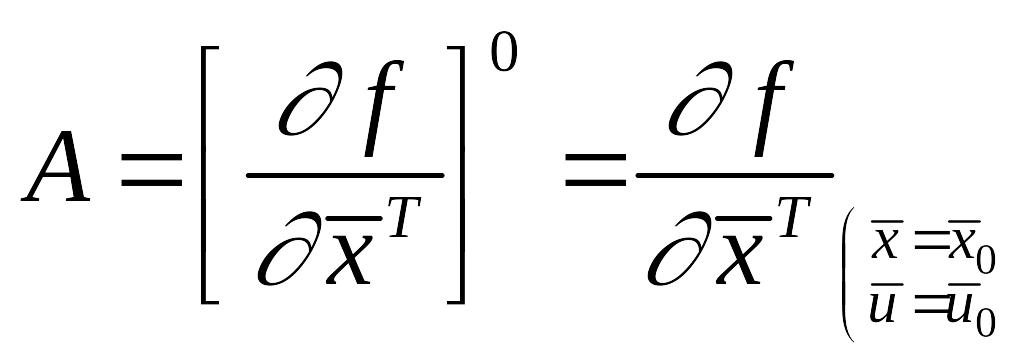. (2.32)
Далее из (2.31) вычтем уравнение статики и отбросим остаточный член R. Тогда получим
Введем обозначение:
.
Тогда (2.21) с учётом (2.32) будет выглядеть так:
.
Последнее уравнение – линейное дифференциальное уравнение в отклонениях.