2.3.1. Дифференциальные уравнения в форме Коши

Задача Коши. Задача Коши, как известно из курса математики, состоит в задании системы дифференциальных уравнений в нормальной форме (разрешенных относительно первой производной) и задании для них граничных (начальных) условий в одной точке.

Использование формы Коши определяется тем, что при решении дифференциальных уравнений удобнее иметь дело не с уравнениями высокого порядка (выше первого), а с системами уравнений первого порядка.

Рассмотрим скалярный объект, поведение которого в динамике описывается дифференциальным уравнением n-го порядка

. (2.17)

Произведем в этом уравнении замену переменных следующим образом:

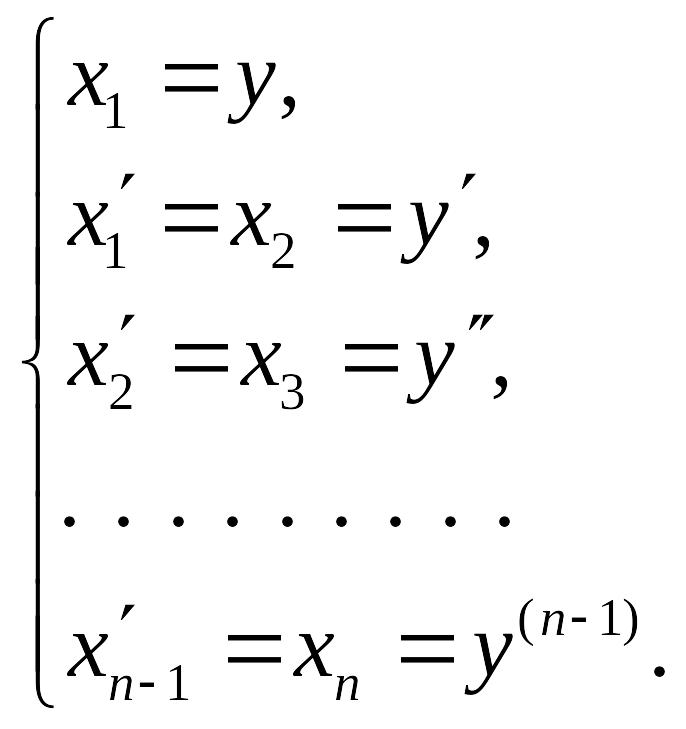(2.18)

и разрешим исходное уравнение относительно старшей производной

или

. (2.19)

Совокупность уравнений (2.18) и (2.19) представляют нормальную форму Коши дифференциального уравнения (2.17). В общем виде полученная система представляется как

(2.20)

где

есть матрица Фробениуса, а матрица

определяет влияние входного воздействия на состояние объекта.

Значение выходного сигнала y объекта определяется в общем случае как состоянием объекта x, так и значением входного воздействия u, так что

.

В общем случае А − функциональная матрица размером n × n, называемая матрицей состояния системы (объекта), В − функциональная матрица размером n × r, называемая матрицей управления (входа), С − функциональная матрица размером m × n, называемая матрицей выхода по состоянию, D − функциональная матрица размером m × r, называемая матрицей выхода по управлению.

Очень часто D = 0, т.е. выход непосредственно зависит от входа и тогда исходная система уравнений приобретает вид

(2.21)

Пример 2.6. Представить дифференциальное уравнение

в форме Коши.

Решение. Вводим новые переменные

,

откуда с учетом исходного уравнения следует

Таким образом, представление исходного уравнения в виде (2.20) приводит к формированию следующих матриц:

■

Пример 2.7. Преобразовать полученное дифференциальное уравнение второго порядка для механической системы (рис. 2.7) в форму Коши.

Решение. Заменим наблюдаемую переменную y на переменную состояния x₁:

(2.21)

Тогда уравнение (2.8) примет следующий вид:

(2.22)

Если уравнение (2.22) разделить относительно производных и проинтегрировать по времени, получим уравнение первого порядка

.

Обозначим

. (2.23)

Продифференцируем последнее выражение

. (2.24)

В итоге получилось два уравнения первого порядка (2.23) и (2.24), дающие описание динамики системы. Совокупность полученной системы уравнений

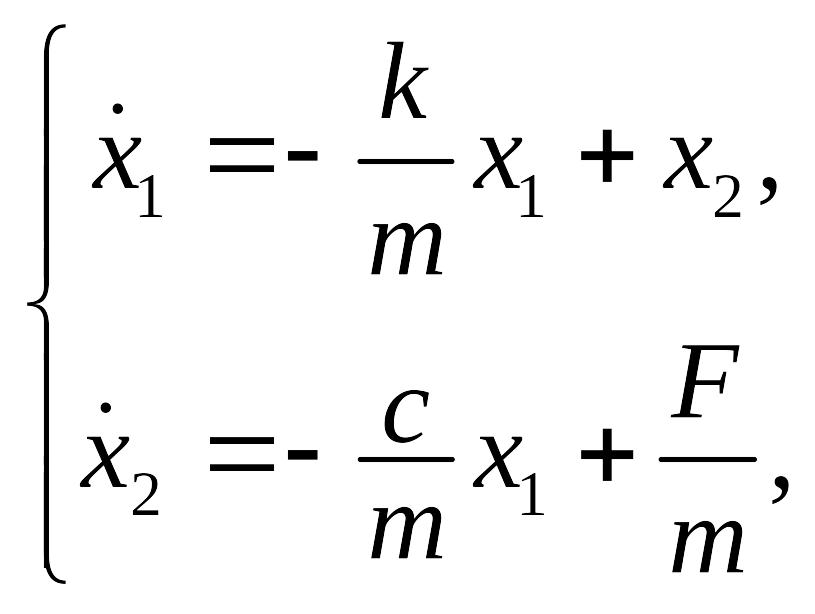(2.25)

совместно с уравнением (2.21), называемым уравнением наблюдения, составляет полное описание поведения объекта в форме Коши.

■

Пример 2.8. Перейти к стандартной форме Коши для рассмотренной

выше электрической системы (рис. 2.1), описываемой системой уравнений

;

.

Решение. Пусть

; ,

тогда из второго уравнения получаем

.

Используя теперь полученное соотношение, запишем первое уравнение в виде

.

В результате получаем систему из двух уравнений первого порядка

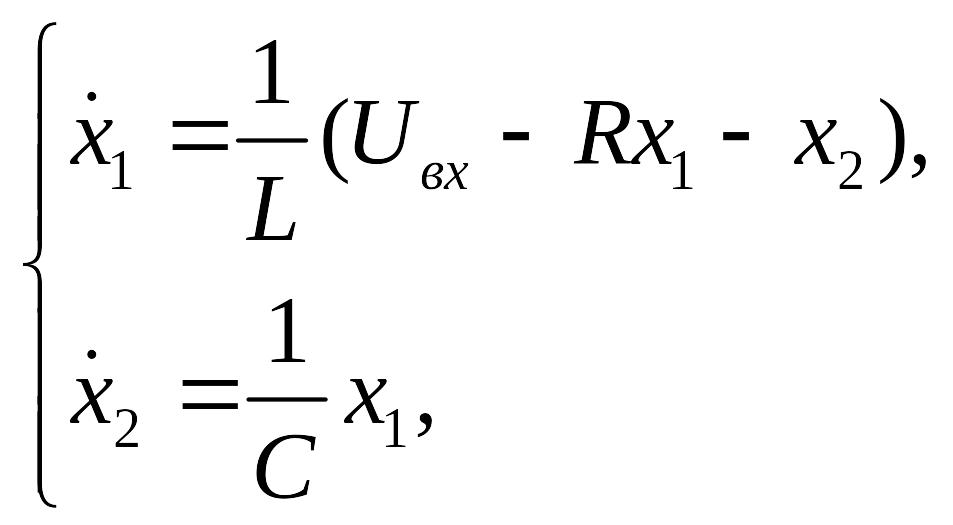
с уравнением наблюдения

.

■

Пример 2.12. Рассмотрим полученную выше систему дифференциальных уравнений механической системы (1.45)

,

и представим ее в матричной форме. Она должна принять вид (2.20):

где:

– вектор состояния, размерности 2,

u – в данном случае, скалярное управление (в общем случае это тоже вектор),

y – в данном случае, также скалярное наблюдение (в общем случае – также вектор).

Сравнивая исходную систему уравнений и конечную форму, видим, что

,

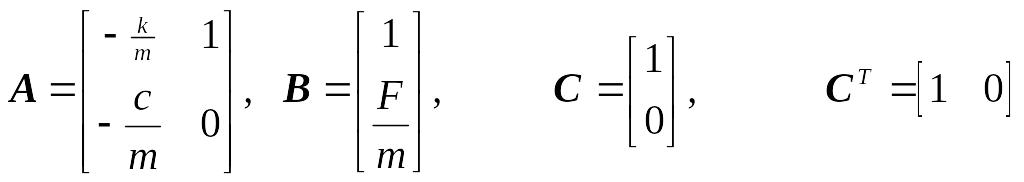следовательно, исходная система уравнений запишется в матричной форме в виде:

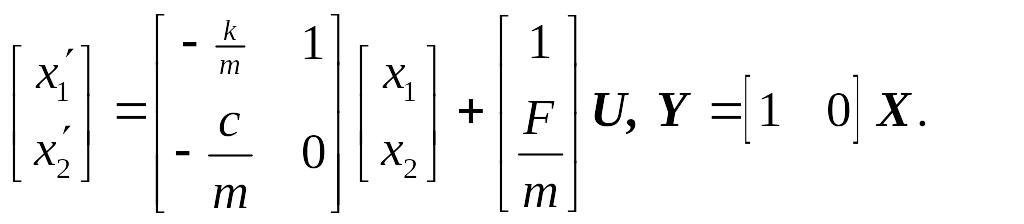
Для решения этой системы уравнений не хватает начальных условий, которые, конечно же, существуют, но не обязательно известны исследователю. Будем считать, что начальные условия известны, и они заданы в одной точке:

Пример 2.13. Получим уравнения состояния для простейшей RLC-цепи, показанной на рис 1.21. Динамическое поведение этой системы при t ≥ t₀ полностью определяется, если известны начальные значения i(t₀), U_c(t₀) и входное напряжение U(t). Следовательно, и можно выбрать в качестве переменных состояния, то есть , . Тогда совокупность исходных уравнений

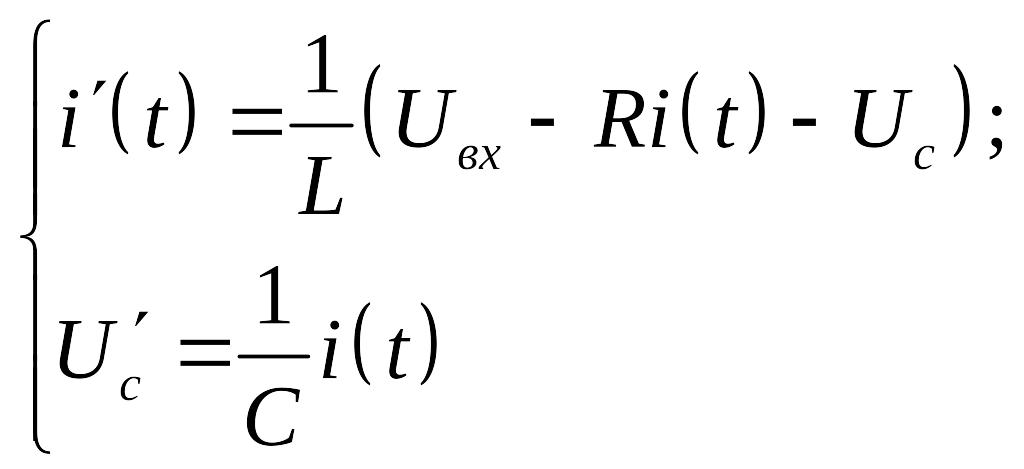
может быть представлена в виде

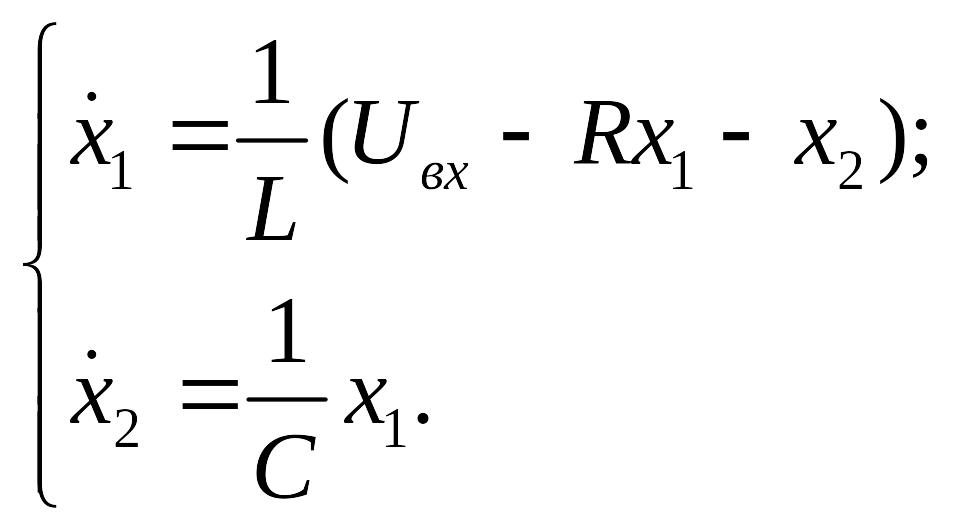
Полученные дифференциальные уравнения можно записать в векторно-матричной форме

Таким образом для рассматриваемой системы матрицы А, В, С векторно-матричной модели будут иметь следующий вид:

; ; .

■

Матричное описание строго формализовано, и не требует понимания физической природы системы. Так же структура модели в "пространстве состояний" не позволяет разобраться во внутренней природе системы. Если эта форма записи дифференциальных уравнений применена обоснованно, то модель, скорее всего, будет истинной.

Передаточная функция в пространстве состояний. Пусть система или какое-либо звено ее в пространстве состояний описываются системой дифференциальных уравнений вида:

, (2.26)

причем для реальных объектов n > m.

Первое уравнение (2.26) можно записать в операторной форме

,

откуда

или

где

– единичная матрица, .

Отсюда

,

где – обратная матрица .

С учетом второго уравнения (2.26) получаем

.

В последнем выражении

(2.27)

есть передаточная функция (функция оператора от p), , т.к. y и u имеют m компонент.

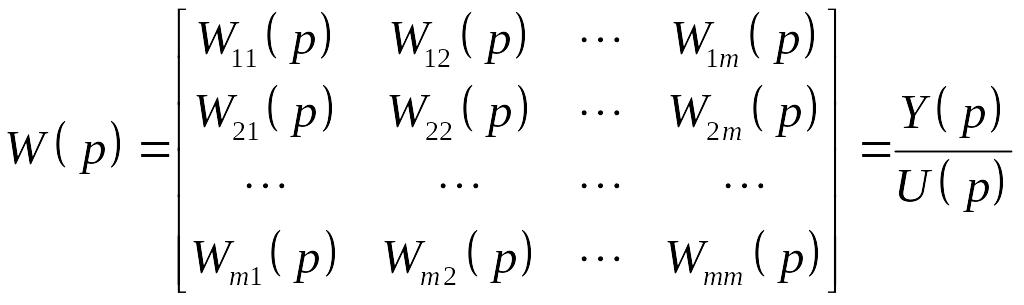
Матричная передаточная функция показывает, какими операторными выражениями связаны между собой компоненты вектора y и u.

.

Если все u_j = 0 и i  j то .

W_ii(p) – собственная передаточная функция i-го канала, отражает соотношение между i-м входом и выходом при нулевых остальных входах.

Если один из элементов матрицы передаточной функции равен 0, то это означает, что в рассматриваемой системе связь между соответствующими компонентами векторов y и u отсутствует.

Пример 2.14. Пусть система описывается системой дифференциальных уравнений

Получить для нее передаточную функцию в форме пространства состояний и в функциональном пространстве.

Решение. Образующие матрицы этой системы есть

.

Передаточная функция системы по определению есть

где

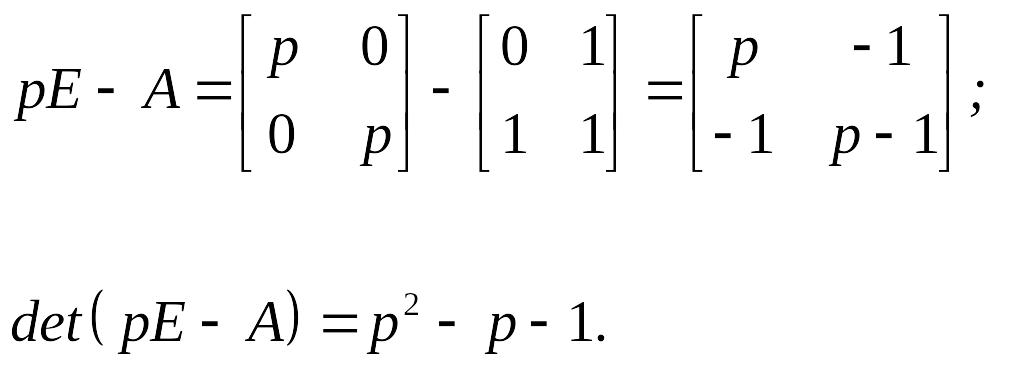
Обратная матрица

,

в которой i, j-элемент получен из выражения

,

где M_ij – минор i, j-элементов. Тогда

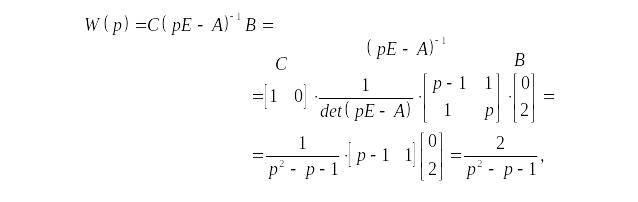
где

– характеристический полином системы;

– характеристическое уравнение системы;

Теперь рассмотрим решение этой задачи в функциональном пространстве. Дифференциальное уравнение системы

в изображениях по Лапласу представляется в виде:

,

откуда

.

■

Построение временных характеристик в форме пространства состояний. Преобразовав по Лапласу систему дифференциальных уравнений системы управления (2.14), получим систему операторных уравнений

и выражение для изображения вектора состояния

. (2.28)

Первое слагаемое (2.28) определяет свободное движение системы, а второе – ее вынужденное движение.

Для получения оригинала (т.е. функции времени ) необходимо выполнить обратное преобразование Лапласа. Оригинал скалярной функции с изображением:

имеет, как нам уже известно, вид экспоненты

.

В матричном случае его аналог

является матричной экспонентой, называемой матрицей перехода.

Произведению изображений соответствует свертка оригиналов, поэтому вектор состояния как функция времени получается из (2.28) в виде

Изображение переменной выхода при нулевых начальных условиях определяется подстановкой второго слагаемого (2.28) во второе уравнение системы (2.26), т.е. в

. (2.28,а)

При подаче на вход системы единичного импульса (U(p) = 1) реакция системы (импульсная переходная функция) выглядит так:

. (2.29)

Сравнивая последнее выражение с выражением для передаточной функции (2.27), видим, что

.

Следовательно, матрицу перехода можно получать путем обращения по Лапласу матрицы .

Пример 2.17. Пусть имеем матрицу состояний нормальной формы

.

Характеристическая матрица запишется как

,

а ее обращение есть

.

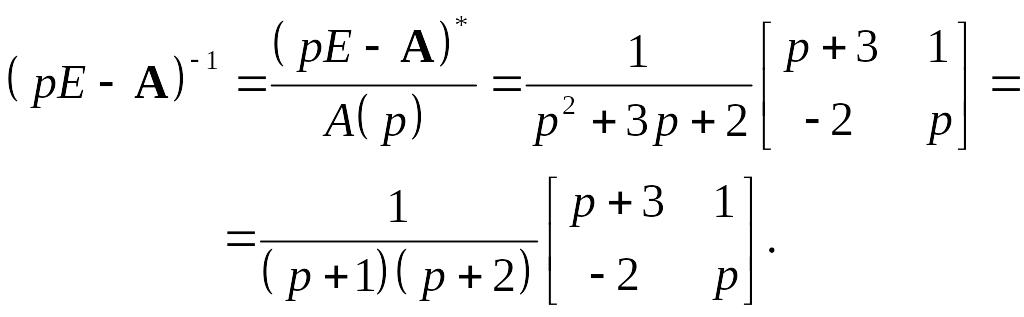Применение обратного преобразования Лапласа к каждому элементу полученной матрицы приводит к получению матрицы перехода

.

Отсюда по формуле (2.29) при известных матрицах входа B = [0 1]^т и выхода C = [2 0] находится функция веса

C B

.

■

Переходная характеристика h(t) есть интеграл от функции веса

.

Построение временных характеристик в форме пространства состояний связано с вычислением матричного экспоненциала (матрицы перехода Ф(t)). Приведенный пример демонстрирует получение элементов Ф(t) путем обратного преобразования Лапласа.

Еще одним способом численного получения значений матрицы перехода при фиксированных значениях t является разложение матричного экспоненциала в степенной ряд

.

Частотные характеристики в форме пространства состояний. Для системы, описываемой системой уравнений (2.26) выходной сигнал может быть описан выражением

.

где

(см. выражение 2.28, а).

Тогда выражения для амплитудной и фазовой частотных характеристик приобретают вид:

,

.

Лекция 7