2.1.5. Полнота характеристик

Пусть оператор преобразования входного воздействия в выход-

ную переменную представлен в форме дифференциального уравнения n-го порядка

или передаточной функции

.

Рассмотрим дифференциальное уравнение для реакции системы на воздействие при нулевых начальных условиях. При , где p_i – корень характеристического полинома , коэффициент при экспоненте равен нулю при любом воздействии. По реакциям такой системы нельзя полностью выявить ее собственные свойства: в них будет отсутствовать составляющая, соответствующая корню p_i. В этом случае говорят, что система по рассматриваемой паре вход-выход является неполной.

Отсюда следует, что временные характеристики – реакции системы на воздействия при нулевых начальных условиях по неполной паре вход-выход – не отражают полностью собственных свойств системы: операторные полиномы A и B дифференциального уравнения неполной системы имеют нетривиальный общий делитель , а передаточная функция системы имеет диполь p_i. Другими словами, если полиномы A и B не являются взаимно простыми, то передаточная функция – вырожденная.

Годографы вырожденных передаточных функций , построенные при изменении аргумента p вдоль некоторого контура C на комплексной плоскости (например, вдоль мнимой оси , ω  0) отражают только полную часть системы.

Потеря собственных свойств особенно существенна, если p_i – правый корень. В этом случае сокращение полиномов недопустимо: при ненулевых начальных условиях, вызванных, например, воздействиями, приложенными к другим входам системы, появляются свободные движения и при они будут содержать составляющую .

Наличие общих делителей в полиномах числителя и знаменателя по выбранной паре вход-выход можно выявить несколькими способами:

– непосредственным вычислением и сопоставление корней полиномов A и B (наилучший способ, здесь также выявляются и приближенные диполи передаточных функций);

– выявлением наибольшего общего делителя полиномов путем деления их по алгоритму Евклида;

– исследованием результанта полиномов – специального определителя прядка mn, построенного из коэффициентов полиномов A и B. Полиномы имеют, по меньшей мере, один общий корень, если их результант равен нулю.

2.3. Средства описания моделей систем управления

в пространстве состояний

Понятие пространства состояний. Современная теория автоматического управления оперирует с векторно-матричными моделями динамических систем. При этом рассматриваются в общем случае многомерные системы, т.е. системы произвольного порядка со многими входами и многими выходами, в связи, с чем широко используются векторно-матричные уравнения и аппарат векторной алгебры.

Собственно система, ее входы и выходы − это три взаимосвязанных объекта, которые в каждой конкретной ситуации определяются соответственно математической моделью системы, заданием множеств входных и выходных переменных.

Для получения векторно-матричной модели (ВММ) исследуемая динамическая система представляется в виде “черного ящика” с некоторым числом входных и выходных каналов (рис. 2.19, а).

Все переменные, характеризующие систему, можно разделить на три группы.

1. Входные переменные или входные воздействия, генерируемые системами, внешними по отношению к исследуемой системе. Они характеризуются вектором входа

,

где γ − число входов.

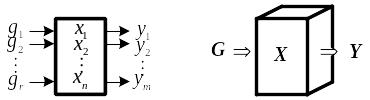
Рис. 2.19. Скалярное (а) и векторное (б) представления динамической системы в виде "черного ящика"

2. Выходные переменные, характеризующие реакцию системы на указанные входные воздействия. Представляются вектором выхода

,

где m − число выходов.

3. Промежуточные переменные, характеризующие внутреннее состояние системы, иначе − переменные состояния, представляются вектором

,

где n − число переменных состояния.

Состояние системы − это та минимальная информация о прошлом, которая необходима для полного описания будущего поведения (т.е. выходов) системы, если поведение ее входов известно.

Совокупность входов можно рассматривать как один обобщенный вход, на который воздействует вектор входа U, совокупность выходов как вектор Y, а совокупность промежуточных координат, характеризующих состояние системы, − как вектор состояния X (см. рис. 2.19, б).

Решение задач анализа и синтеза связано с исследованием состояний системы, множество которых образует пространство состояний, .

Исследование в пространстве состояний – это определение выходной реакции системы (совокупности значений выходных сигналов) для любой из допустимых совокупностей значений входных сигналов (вектора входа) и сигналов (векторов) состояния системы.

Дифференциальные уравнения в форме пространства состояний – это матричная форма записи системы дифференциальных уравнений, адаптированная для теории управления путем выделения из формы Коши алгебраических уравнений, связывающих внутренние координаты системы управления с выходной(ыми).