2.2.4. Частотные характеристики

Преобразование Фурье. При исследовании и создании систем управления, аппарат частотных характеристик был применен одним из первых, т.к. они наиболее полно отражают физическую природу процессов, происходящих в динамических объектах.

Преобразованием Фурье функции f(t) служит функция F(jω), определяемая в виде

.

Преобразование Фурье позволяет разложить непериодическую функ-

цию f(t) для которой выполняется условие сходимости

,

означающее, что интеграл существует, в бесконечный ряд гармоник, образующих непрерывный спектр частот в интервале от – до + с бесконечно малым интервалом частот между смежными частотами (  0).

Понятие о частотных характеристиках. Частотные характеристики – реакции элементов или систем на входные гармонические сигналы единичной амплитуды во всем диапазоне частот. В линейных системах форма и частота установившейся реакции совпадают с формой и частотой входного сигнала (с изменением частоты меняются только амплитуда и фаза).

Пусть на вход любой системы подан сигнал синусоидальной формы:

f(t) = X_m cos(t) = X_m e ^jt .

Воспользовавшись формулами Эйлера, последнее выражение можно представить в виде

.

В силу линейности системы под воздействием этого сигнала по истечении времени окончания переходных процессов на выходе системы (звена) установится также гармонический выходной сигнал той же частоты, но сдвинутый по фазе относительно входной величины на некоторый угол , который также можно представить в виде

.

В соответствии с принципом суперпозиции прохождение составляющих и можно рассматривать независимо друг от друга. Более того, соотношения между и , а также между и совпадают, так что достаточно рассмотреть одно из этих соотношений. Поэтому под воздействием и реакцией системы на воздействие будем понимать функции

f(t) = X_m e ^jt

и

y(t) =Y_m e ^{jt+)}.

Рассмотрим переход от дифференциального уравнения n-го порядка и передаточной функции к частотным характеристикам.

Установившаяся реакция линейной системы на гармоническое воздействие единичной амплитуды

соответствует частному решению неоднородного дифференциального уравнения

или в операторной форме

.

Найдем это решение в виде

y(t) =R(ω) e ^{jt) + ω},

где R(), () – амплитуда и фаза, зависящие в общем случае от частоты.

Поскольку

,

…………………

а также поскольку

,

………………………

то, подставив эти соотношения в операторную форму неоднородного дифференциального уравнения, получим

или после деления обеих частей на exp{jt}

.

Полученное комплексное соотношение, модуль которого равен отношению амплитуд выходной величины к входной

,

а аргумент – сдвигу фазы выходной величины по отношению к входной

,

называется комплексной частотной передаточной функцией (комплексной частотной характеристикой).

Отсюда также следует переход от передаточной функции к частотным характеристикам: комплексная частотная характеристика получается заменой p → j аргумента передаточной функции

.

Вычисление значений частотных характеристик для конкретного p =  + j сводится к вычислению значений полиномов A(p) и B(p) и делению полученных комплексных значений друг на друга. В результате получаются значения вещественной P() и мнимой Q() частотных характеристик. Значения амплитудной характеристики вычисляются как

,

а фазовой частотной характеристики – как

.

Напомним, что график функции имеет вид, показанный на рис. 2.12.

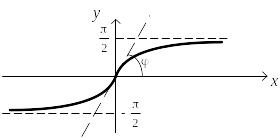
Рис. 2.12. График функции

Поэтому все частотные характеристики – это арктангенсоиды своего аргумента.

Поскольку значения () определяются на интервале (−, ), то в случае систем высокого порядка истинные значения определяются в предположении о том, что в пределах выбранного шага частот () не изменяется на , т.е. корни полиномов A(p) и B(p) располагаются достаточно далеко от мнимой оси.

Пример 2.5. Пусть звено описывается дифференциальным уравнением

.

Используя предыдущие выражения, найдем производные

.

Подставим сигнал в уравнение движения:

(T₂²(j)² + T₁(j) + 1) Y_m e ^{jt+)} = (k₁ + k₂(j)) X_m e ^jt

и найдем отношение выходного сигнала к входному:

■

Совокупность амплитудной и фазовой частотных характеристик называется ее амплитудно-фазовой характеристикой, или годографом (Найквиста). Пример амплитудно-фазовой характеристики приведен на рис.2.13.

Рис. 2.13. Пример амплитудно-фазовой характеристики

Здесь же показана развертка R() и Q() в диапазоне частот. Из рисунка следует, что амплитудно-фазовая характеристика есть фронтальная проекция ее развертки в частотной области на комплексную плоскость.

Из рис. 2.13 также видно, что с ростом частоты реальные системы хуже пропускают сигналы – ослабляют амплитуду и вносят отрицательный

фазовый сдвиг.

Отметим следующие соотношения, существующими между преобразованиями Лапласа и Фурье:

 по сравнению с преобразованием Лапласа преобразование Фурье позволяет отобразить оригинал только на мнимую ось, в преобразовании Лапласа же используется вся комплексная плоскость;

 частотная передаточная функция получается из обычной передаточной функции заменой оператора Лапласа p на комплексную частоту j, т.е. в результате перехода от изображения Лапласа к изображению Фурье;

 дифференциальное уравнение движения системы связывает входной и выходной сигналы (т.е. функции времени), передаточная функция связывает изображения Лапласа тех же сигналов, а частотная передаточная функция связывает их спектры.

Понятие о логарифмических частотных характеристиках. Прологарифмируем выражение частотной передаточной функции

.

Отсюда видно, что вещественной частью частотной передаточной характеристики является логарифм модуля, а мнимой – фаза. Такое представление частотной передаточной функции называется логарифмическим.

При исследовании систем управления, амплитудную и фазовую частотные характеристики удобно строить в логарифмических координатах. Это связано с двумя обстоятельствами:

1. В логарифмических масштабах кривизна характеристик резко уменьшается, что позволяет в большинстве практических случаев приближенно изображать амплитудную частотную характеристику ломаными линиями.

2. В логарифмических масштабах амплитудная частотная характеристика цепочки звеньев равна сумме амплитудных частотных характеристик отдельных звеньев

.

В качестве единицы измерения в логарифмическом масштабе принят Бел – единица измерения десятичного логарифма коэффициента усиления мощности сигнала. 1 Бел соответствует усилению мощности в 10 раз, 2 Бела – в 100 раз и т.д. Так как мощность сигнала пропорциональна квадрату амплитуды A² (например, для электрической цепи ), а , то усиление в Белах, выраженное через отношение амплитуд A, равно . Поскольку Бел – весьма большая величина, то в качестве единицы измерения при построении логарифмических амплитудных частотных характеристик служит децибел, равный 0,1 Бела, и тогда усиление мощности в децибелах равно

Амплитудная частотная характеристика в логарифмических масштабах строится в координатах 20lgA и lg, а фазовая частотная характеристика – в виде зависимости  от lg.

При построении амплитудных частотных логарифмических характеристик (рис. 2.14) по оси абсцисс откладывается в логарифмическом масштабе частота (десятичный логарифм) (изменение частоты в 10 раз – декада), а около отметок указывается само значение частоты, а по оси ординат также в логарифмическом масштабе – 20 lg амплитуды.

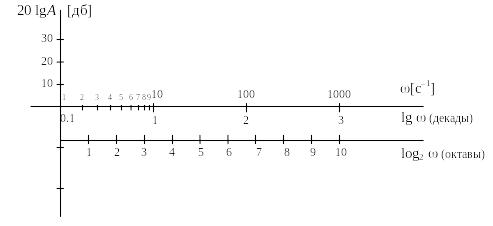
Рис. 2.14. Логарифмические координаты для амплитудной частотной характеристики

Иногда применяется логарифм частоты при основании 2 (изменение

частоты в два раза – октава) одна октава равно 0,303 декады, т.к. .

Для построения логарифмических фазовых характеристик на оси абсцисс используется аналогичная шкала частот или , а по оси ординат (обычно используется нижняя часть плоскости) откладывается фаза  в градусах. При практических расчетах оказывается удобным совмещать точку нуля децибел с точкой фазы – 180˚(рис. 2.15).

Рис. 2.15 . Совмещение координат логарифмических амплитудной и частотной характеристик

Отметим ещё, т.к. точка в логарифмическом масштабе находится слева в –  (lg 0 = – ∞), то логарифмические амплитудная и фазовая частотные характеристики строятся не от , а от достаточно малого, но конечного значения , которое и откладывается в начале координат.

Лекция 6

Построение логарифмических частотных характеристик. Частотные характеристики – амплитудную R() и фазовую () – можно получать экспериментально путем подачи на вход объекта гармонических воздействий в существенном для системы диапазоне частот. Методы спектрального анализа позволяют оценить значения частотных характеристик путем обработки временных последовательностей на входе и выходе объекта.

В качестве иллюстрации рассмотрим несколько важных примеров.

1. Пусть модуль частотной передаточной функции равен постоянному числу

.

Тогда логарифмическая амплитудная частотная характеристика определится как

и представляет собой прямую, параллельную оси абсцисс (ее значение не зависит от частоты), как показано на рис.2.16.

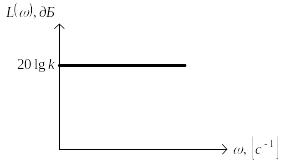
Рис. 2.16. Логарифмическая амплитудная частотная характеристика звена с частотной передаточной функцией

2. Пусть , тогда .

При , при . Таким образом, это – прямая линия, проходящая через точку с координатами и имеющая отрицательный наклон 20 дБ/дек, как показано на рис. 2.17. Частота, соответствующая переходу логарифмической характеристики через ось частот (в ней ), равна

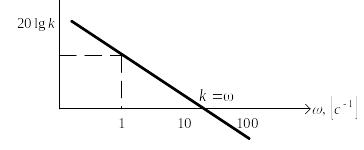
Рис. 2.17. Логарифмическая амплитудная частотная характеристика звена с частотной передаточной функцией

С увеличением степени ω на единицу наклон прямой увеличивается на – 20 дБ/дек, т.к.

и т.д.

3. Пусть , тогда

.

При , при . Таким образом, это – прямая линия, проходящая через точку с координатами и имеющая положительный наклон 20 дБ/дек, как показано на рис. 2.18. Частота, соответствующая переходу логарифмической характеристики через ось частот (в ней ), равна . Поскольку , то эта частота является отрицательной.

Рис. 2.18. ЛАЧХ звена с частотной передаточной функцией

С увеличением степени ω на единицу наклон прямой увеличивается на 20 дБ/дек, т.к.

и т.д.