9 Напряжения в наклонных к оси сечениях стержня.

Рассечем растянутый стержень плоскостью, наклоненной к поперечному сечению под углом (рис. 4.19, а), и рассмотрим равновесие нижней отсеченной части (рис. 4.19, б). Из уравнения равновесия несложно установить, что равнодействующая внутренних сил в наклонном сечении направлена по оси стержня и равна внешней силе, т. е. .

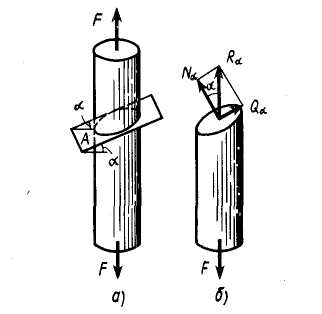
Рис. 4.19. Схемы сил упругости в наклонном сечении стержня

Разложим эту равнодействующую на нормальную и касательную составляющие.

Учитывая, что площадь наклонного сечения (А – площадь нормального сечения), и полагая, что нормальные и касательные напряжения распределены по наклонному сечению также равномерно (как по поперечному сечению), получим

Эти соотношения устанавливают связь между напряжениями и в «косых» сечениях и напряжением в нормальном к оси сечении растянутого стержня. Видно, что максимальные нормальные напряжения действуют в поперечных сечениях стержня ( ). Поэтому расчеты прочности стержней в условиях растяжения (сжатия) выполняют по нормальным напряжениям в поперечных сечениях.

В наклонных сечениях растянутого (сжатого) стержня действуют одновременно как нормальные, так и касательные напряжения. Значения этих напряжений зависят от угла наклона . Максимальные (по абсолютной величине) касательные напряжения будут на площадках при , . Нормальные напряжения на этих площадках равны касательным.

Этот вывод имеет важное практическое значение. Некоторые конструкционные материалы (например, пластичные стали) хуже сопротивляются деформациям сдвига, чем деформациям растяжения. В связи с этим максимальные касательные напряжения могут вызывать разрушение деталей из таких материалов.

В продольной плоскости ( ) как нормальные, так и касательные напряжения отсутствуют.

В двух любых взаимно перпендикулярных плоскостях алгебраическая сумма нормальных напряжений равна нормальному напряжению а в поперечном сечении, а касательные напряжения равны между собой по абсолютной величине и противоположны по направлению (знаку). Последнее условие является общей особенностью любого напряженного состояния и носит название закона парности касательных напряжений.

9 Напряженное и деформированное состояние в точке.

Ранее рассматривалось, что при одноосном растяжении (сжатии) стержня на некоторых площадках одновременно действуют нормальные и касательные напряжения, значения которых зависят от угла наклона к оси стержня этих площадок. Имеются также площадки (сечения), в которых касательные напряжения отсутствуют. На этих площадках нормальные напряжения имеют экстремальные значения: максимальные в сечениях, перпендикулярных оси стержня , и минимальные (при растяжении равны нулю) в сечении, параллельном оси стержня _.

Площадки, в которых отсутствуют касательные напряжения, называются главными. Нормальные напряжения, действующие по этим площадкам, также называют главными.

В других более сложных случаях действия сил на стержень также возникает задача об определении главных площадок и максимальных напряжениях на них, Для этого требуется исследовать напряженное состояние в некоторых характерных точках деформированного тела, т. е. определить совокупность напряжений, действующих по всевозможным площадкам, проведенным через указанные точки.

Центральное растяжение (сжатие) стержня является простейшим видом деформации тела, при котором лишь одно из главных напряжении не равно нулю. Такой вид напряженного состояния называют иногда линейным. На практике встречаются виды деформации, когда в окрестности какой-либо точки тела действуют два и даже три главных напряжения. Напряженное состояние в точке в этих случаях называют соответственно плоским и объемным.

Рассмотрим плоское напряженное состояния, которое реализуется в элементах конструкции сравнительно часто, например, в точках поверхностей деталей машин.

Рассмотрим тонкую пластинку (рис. 4.20) под действием внешних сил в системе координат Oxyz. Ее поверхности, перпендикулярные оси z, свободны от внешних сил. В окрестности произвольной точки К сечениями, перпендикулярными плоскостям этой пластинки, мысленно вырежем элементарный параллелепипед. Со стороны пластинки на этот параллелепипед будут действовать в общем случае нормальные и касательные усилия. Векторы нормальных и касательных напряжений, соответствующие этим условиям, будут также лежать в одной плоскости, образуя в окрестности точки K плоское напряженное состояние.

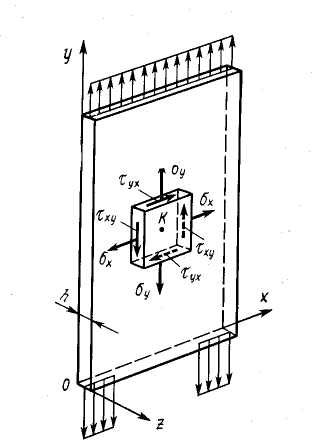
Рис. 4.20. Плоское напряженное состояние

Плоское напряженное состояние в каждой точке тела путем поворота осей может быть представлено как растяжение-сжатие в двух взаимно перпендикулярных направлениях напряжениями и (рис. 4.21, а), третье главное напряжение .

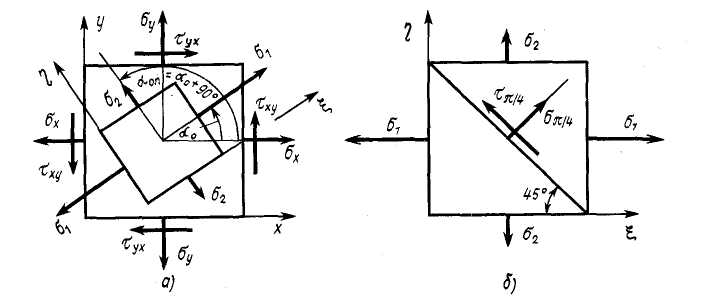
Рис. 4.21. Главные напряжения и главные площадки

Складывая почленно соотношения (6), получим

,

т. е. сумма нормальных напряжений на двух взаимно перпендикулярных площадках не зависит от угла .

Максимальное и минимальное касательные напряжения равны по величине и отличаются лишь знаком.

,

Максимальное значение касательных напряжений равно абсолютному значению полуразности главных напряжений.

В площадках, где действуют максимальные касательные напряжения, имеются и нормальные напряжения (рис. 4.21, а).

Определим деформации и в направлении главных напряжений при плоском напряженном состоянии. Для этого используем закон Гука для линейного напряженного состояния

,

зависимость между продольной и поперечной деформациями

и принцип независимости действия сил.

Напряжение вызывает продольную деформацию

и поперечную деформацию (в направлении напряжения )

.

Напряжение вызывает деформации

.

Суммируя деформации одного направления, получим

– закон Гука для плоского напряженного состояния.

Аналогично для объемного напряженного состояния (рис. 4.22)

– закон Гука для объемного напряженного состояния.

здесь и – третье главное напряжение и главная деформация.

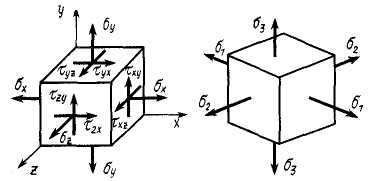
Рис. 4.22. Объемное напряженное состояние