
- •2 Надежность машин и механизмов как важнейшее эксплуатационное свойство
- •Объекты проектирования на микроуровне
- •3. Основные понятия и принципы сопротивления материалов.
- •4.2. Напряженно-деформированное состояние тела. Метод сечений.
- •4. Растяжение-сжатие.
- •6 Сдвиг.
- •6. Кручение.
- •7. Изгиб.
- •8 Прочность при переменных напряжениях. Кривая усталости, предел выносливости
- •5 Испытания материалов при растяжении. Диаграмма растяжения.
- •9 Напряжения в наклонных к оси сечениях стержня.
- •9 Напряженное и деформированное состояние в точке.
- •9 Теории прочности.
7. Изгиб.
Изгибом стержня называется изменение кривизны его продольной оси. Изгиб яляется плоским, если ось стержня остается кривой линией, расположенной в одной плоскости. Изгиб при отсутствии поперечной силы называется чистым. Изгиб при наличии поперечных сил называют поперечным изгибом.
Чистый прямой изгиб характеризуется тем, что на выпуклой стороне волокна растягиваются, а на вогнутой – сжимаются. Свойства бруса при растяжении и сжатии одинаковы (на основании допущения об изотропии материалов). Переход от растяжения к сжатию происходит непрервывно и таким образом должен существовать нейтральный слой, длина которого не меняется. При чистом изгибе происходит поворот поперечных сечений без их искажения.
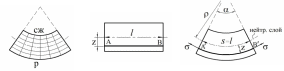
Рис. 4.11. Деформация изгиба
Относительное
удлинение слоя, удаленного на расстояние
 от нейтрального слоя, равно
от нейтрального слоя, равно
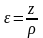 .
Используя закон Гука, записываем
.
Используя закон Гука, записываем
 .
.
Отношение
 является постоянным для конкретного
материала и конкретного случая изгиба,
поэтому напряжения являются линейной
функцией координаты
.
Из условия равновесия между силовыми
факторами и внутренними силами:
является постоянным для конкретного
материала и конкретного случая изгиба,
поэтому напряжения являются линейной
функцией координаты
.
Из условия равновесия между силовыми
факторами и внутренними силами:
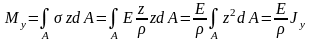 ,
,
где
 – осевой момент инерции сечения.
– осевой момент инерции сечения.
Домножим и разделим на , тогда плучим
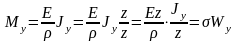 ,
,
где
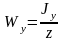 – осевой
момент сопротивления поперечного
сечения стержня (для круглого стержня
– осевой
момент сопротивления поперечного
сечения стержня (для круглого стержня
 ,
,
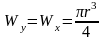 ).
).
Формула
для определения нормальных напряжений
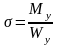 .
Максимальные нормальные напряжения
.
Максимальные нормальные напряжения
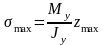 (рис. 4.12, а).
(рис. 4.12, а).
В результате условие прочности при изгибе
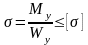 .
.
Формула для проектного расчета
 .
.
Если
поперечный изгиб вызывается внешней
силой
 ,
то в рассматриваемом сечении будет
возникать поперечная сила
(рис. 4.12, б),
от действия которой в сечении будут
возникать контактные напряжения. Их
величина определяется по формуле
,
то в рассматриваемом сечении будет
возникать поперечная сила
(рис. 4.12, б),
от действия которой в сечении будут
возникать контактные напряжения. Их
величина определяется по формуле
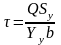 ,
где
,
где
 –
статическй
момент площади сечения относительно
оси
–
статическй
момент площади сечения относительно
оси
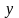 .
.

Рис. 4.12. Напряжения при изгибе
Внутренние слои материала, особенно вблизи нейтральной линии (см. рис. 4.11), мало напряжены. Поэтому при проектировании стержней, испытывающих деформации изгиба, стремятся к использованию сечений с возможно большими моментами инерции относительно нейтральной оси. Для этого необходимо распределять площадь сечения подальше от нейтральной оси.
На рис. 4.13 в качестве примера показаны экономичные стандартные профили сечений стальных прокатных балок, выпускаемых металлургическими предприятиями для нужд промышленности и строительства.

Рис. 4.13. Рациональные сечения стержней при изгибе: а — двутавр; б — швеллер; в — уголок
8 Прочность при переменных напряжениях. Кривая усталости, предел выносливости
Большинство деталей машин в рабочих условиях испытывают переменные напряжения, циклически изменяющиеся во времени (циклические напряжения). Они возникают в деталях от изменения нагрузки, а также в связи с изменением положения их сечений по отношению к постоянной нагрузке (например, при вращении детали).
Законы изменения переменных напряжений могут быть различными, но все их можно представить в форме простейших гармоник синусоиды или косинусоиды.
На
рис. 4.14 показано периодическое изменение
напряжений во времени от наибольшего
значения
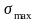 до
наименьшего
до
наименьшего
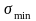 и
обратно. Переменные напряжения могут
быть также касательными и изменяться
от
и
обратно. Переменные напряжения могут
быть также касательными и изменяться
от
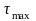 до
до
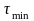 .
.
Число циклов напряжений в секунду называют частотой нагружения. Циклы напряжений могут быть знакопостоянными (рис; 4.14, а, в) или знакопеременными (рис. 4.14, б).
Любой цикл напряжений может быть охарактеризован средним напряжением
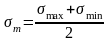 ;
;
 ,
,
амплитудой переменного напряжения
 ;
;
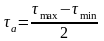 .
.

Рис. 4.14. Циклы переменных напряжений
Важной характеристикой является коэффициент асимметрии цикла
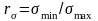 ;
;
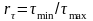 .
.
Если
наибольшее и наименьшее напряжения
одинаковы по величине и обратны по
знаку, то
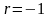 и
цикл изменения напряжений называется
симметричным
(рис.
4.14,6).
Здесь
и
цикл изменения напряжений называется
симметричным
(рис.
4.14,6).
Здесь
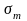 и
и
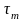 равны
нулю. Если
наименьшее напряжение равно нулю, то
равны
нулю. Если
наименьшее напряжение равно нулю, то
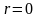 и цикл называется пульсационным
(рис.
4.14, в).
и цикл называется пульсационным
(рис.
4.14, в).
Опыт показывает, что при переменных напряжениях после некоторого числа циклов может наступить внезапное разрушение детали без заметных остаточных деформаций при напряжениях, значительно меньших предела прочности материала. Это явление называется усталостью материалов.
Число циклов до момента разрушения зависит от амплитуды напряжений и меняется в весьма широких пределах. Имеют место случаи, когда деталь разрушается при больших напряжениях через несколько циклов, а при меньших напряжениях способна работать неограниченно долго.
Теоретический анализ усталостной прочности связан с большими трудностями. Для создания достаточно стройной теории усталостной прочности необходимо проникнуть в особенности строения кристаллов и межкристаллических связей с последующим привлечением аппарата статистики и теории вероятности.
Экспериментально установлено, что усталостное разрушение начинается с накопления повреждений на границах зерен материала и образования на поверхности в зоне концентрации напряжений микротрещины, не видимой невооруженным глазом. Со временем происходит развитие трещины и ослабление сечения. Трещина растет обычно в направлении, перпендикулярном линии действия наибольших нормальных напряжений. Когда прочность оставшейся (неповрежденной) части сечения становится недостаточной, происходит внезапное разрушение детали.
Способность материала или детали противостоять действию переменных нагрузок называют сопротивлением усталости. Его оценивают с помощью предела выносливости, определяемого экспериментально на специальных машинах или стендах.
На рис. 4.15 показана схема одной из испытательных машин, в которой вращающийся образец 1 находится в условиях чистого изгиба. Образец зажимается во вращающихся цангах 2 и 3. Усилие передается от груза, подвешенного на серьгах 4 и 5. Счетчик 6 фиксирует число оборотов образца. При поломке образца происходит автоматическое отклонение двигателя 7 от контакта 8.

Рис. 4.15. Схемы машины для усталостных испытаний при изгибе
Для
проведения стандартных испытаний на
усталость необходимо иметь не менее
десяти одинаковых образцов. Первый
образец устанавливается на машину и
нагружается симметричным циклом с
амплитудой напряжения, равной
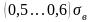 (где
(где
 – предел прочности испытуемого
материала). В момент поломки образца
фиксируется число циклов по счетчику
машины. Второй образец нагружается
амплитудой напряжений меньшей, чем был
нагружен первый образец, и он разрушится,
отработав большее число циклов. Снижая
нагрузку, испытывают следующие образцы.
Испытания заканчивают, когда в результате
постепенного снижения амплитуды
напряжений и увеличения числа циклов
нагружения находят такую амплитуду
напряжений, при которой очередной
образец не разрушился после 107
циклов нагружений. Такое
число
циклов
для стальных образцов считается базовым.
Если
стальной образец выдержал десять
миллионов циклов, то полагают, что он
может выдержать без разрушения и большее
число циклов.
– предел прочности испытуемого
материала). В момент поломки образца
фиксируется число циклов по счетчику
машины. Второй образец нагружается
амплитудой напряжений меньшей, чем был
нагружен первый образец, и он разрушится,
отработав большее число циклов. Снижая
нагрузку, испытывают следующие образцы.
Испытания заканчивают, когда в результате
постепенного снижения амплитуды
напряжений и увеличения числа циклов
нагружения находят такую амплитуду
напряжений, при которой очередной
образец не разрушился после 107
циклов нагружений. Такое
число
циклов
для стальных образцов считается базовым.
Если
стальной образец выдержал десять
миллионов циклов, то полагают, что он
может выдержать без разрушения и большее
число циклов.
По
результатам испытаний строят кривую
усталости
(рис.
4.16). Наибольшее
значение максимального напряжения
цикла, которое образец выдерживает до
базы испытаний, называют пределом
выносливости.
При
симметричном цикле предел выносливости
обозначается через
 ,
при пульсирующем –
,
при пульсирующем –
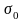 ,
а при асимметричном –
,
а при асимметричном –
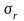 .
.

Рис. 4.16. Кривая усталости
Для
расчета деталей, не предназначенных на
длительный срок службы, вводится понятие
ограниченного
предела выносливости
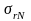 ,
где
,
где
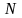 – заданное число циклов (меньше базового).
– заданное число циклов (меньше базового).
Пределы выносливости определяются для различных видов деформации: растяжение (сжатие), изгиб и кручение. На основании большого числа испытаний установлены приближенные зависимости между пределом выносливости при изгибе и пределами выносливости для других видов деформации:
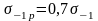 ;
;
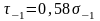 .
.
где
 – предел выносливости при симметричном
цикле растяжения-сжатия;
– предел выносливости при симметричном
цикле растяжения-сжатия;
 – предел выносливости при кручении в
условиях симметричного цикла.
– предел выносливости при кручении в
условиях симметричного цикла.
Зависимость между переменным напряжением и числом циклов до разрушения достаточно точно описывается уравнением
 ,
,
где
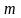 и
и
 – постоянные для данного материала,
температуры и окружающей среды;
– постоянные для данного материала,
температуры и окружающей среды;
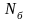 – базовое число циклов.
– базовое число циклов.
В логарифмических координатах уравнение кривой усталости
 ,
,
тангенс
угла
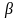 наклона прямой (см. рис. 4.16)
наклона прямой (см. рис. 4.16)
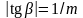 .
.
С
увеличением значения
наклон прямой к оси
 уменьшается и при
уменьшается и при
 прямая становится горизонтальной.
Обычно
прямая становится горизонтальной.
Обычно
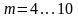 .
.
Учитывая,
что уравнение
справедливо и для точки
перегиба кривой усталости, т. е.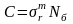 получим
получим
 ,
,
откуда
 .
.
Эта зависимость используется для определения ресурса работы элементов конструкций при известном уровне рабочих переменных напряжений и значениях и .
