4. Растяжение-сжатие.

Растяжением (сжатием) называется такой вид деформации, при котором в поперечном (перпендикулярном оси) сечении стержня возникает только продольная растягивающая (сжимающая) сила.

В условиях растяжения будет находиться стержень под действием осевых сил на краях (рис. 4.7, а). Модель растягиваемого стержня широко используется в расчетах болтов, ремней передач, стержней ферм, лопаток турбин и др.

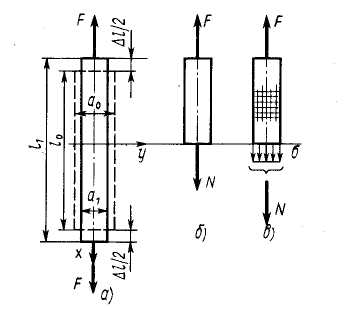
Рис. 4.7. Схемы деформации (а), внутренних сил (б) и напряжений в сечении (в) стержня при растяжении

Для определения продольной силы N используется метод сечений. Условимся считать эту силу положительной (т. е. присвоим знак плюс), если она растягивает стержень, и отрицательной – если сжимает.

Для определения силы N в сечении стержня (рис. 4.7, а) рассмотрим равновесие верхней отсеченной части (рис. 4.7. б). Составляя уравнение равновесия, получим ; 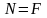. Знак плюс показывает, что стержень растянут.

Сила N, приложенная в центре тяжести произвольного сечения стержня (см. рис. 4.7, б), является равнодействующей внутренних сил , действующих на бесконечно малые площадки поперечного сечения площадью А:

.

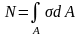Из этого уравнения нельзя найти закон распределения нормальных напряжений по поперечному сечению. Однако если предположить, что плоские поперечные сечения стержня смещаются при растяжении параллельно начальным положениям, оставаясь плоскими (гипотеза плоских сечений), то нормальные напряжения во всех точках сечения должны быть одинаковыми, т. е. .

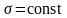Эта гипотеза, высказанная голландским ученым Д. Бернулли, позднее была подтверждена экспериментами. Так, если на поверхность стержня нанести систему взаимно перпендикулярных линий (см. рис. 9, в), то после его нагружения эти линии переместятся параллельно самим себе.

Учитывая эту гипотезу, получим 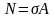, откуда

.

Таким образом, нормальное напряжение в поперечном сечении стержня при растяжении равно поделенной на площадь сечения продольной силе в этом же сечении.

При сжатии стержня напряжения имеют лишь другой (отрицательный) знак (нормальная сила направлена в тело стержня).

Что касается деформаций, то стержень постоянного сечения площадью А под действием осевых растягивающих сил (см. рис. 4.7) удлиняется на величину

,

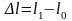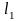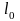где и – длины стержня в деформированном и недеформированном состоянии.

Это приращение длины называется полным или абсолютным удлинением (укорочением). Экспериментально установлено, что чем больше , тем больше . Поэтому наиболее удобной мерой деформации является относительное удлинение, т. е. удлинение, отнесенное к первоначальной длине стержня, называемое линейной деформацией:

.

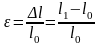Величина 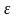обычно выражается в процентах от начальной длины.

Опыты показывают также, что удлинение стержня в осевом направлении сопровождается уменьшением его поперечных размеров (см. рис. 4.7, а).

Следовательно, при растяжении и сжатии возникает не только продольная, но и поперечная деформация стержня.

Если первоначальная ширина стержня была 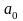, то под действием сил F она уменьшится на величину 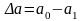. Относительная поперечная деформация будет

.

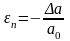Знак минус показывает, что при растяжении стержня поперечные размеры уменьшаются.

Отношение поперечной деформации к продольной при растяжении (сжатии), взятое по абсолютной величине, называют коэффициентом Пуассона (по имени французского ученого, установившего взаимосвязь деформаций)

.

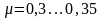На основании экспериментов получено: для сталей , для алюминиевых сплавов , для медных сплавов .

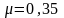В результате условие прочности при растяжении

,

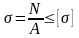где 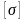– допускаемое значение растяжения.

Для проектного расчета:

.

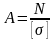Условие жесткости при растяжении

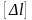– допускаемое удлинение.

Принято считать сжатие эквивалентным растяжению.

Формула для проектного расчета .

Закон Гука для центрального растяжения (сжатия)

Связь между напряжением и деформацией установлена английским ученым Р. Гуком в конце XVI в.: деформации материала элемента в каждой его точке прямо пропорциональны напряжениям в этой же точке как в процессе нагружения, так и при разгрузке.

Этот закон справедлив для большинства материалов и имеет вид:

,

где Е — коэффициент пропорциональности, именуемый модулем упругости.

По физическому смыслу модуль упругости – напряжение, которое вызывает деформацию 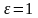(удлинение стержня, равное первоначальной длине).

По данным экспериментов:

E = (2...2,2)10⁵ МПа – для сталей;

E = 1,110⁵ МПа – для титановых сплавов;

E = 0,710⁵ МПа – для алюминиевых сплавов.

Учитывая, 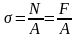, а с другой стороны , абсолютная деформация растянутого (сжатого) стержня:

.

Произведение ЕА называют жесткостью сечения стержня при растяжении.